
ここ数十年で、世界経済は金融危機の渦に定期的に陥りました。 1987年、1997年、2008年には、既存の金融システムがほぼ崩壊しました。そのため、主要な専門家は、金融の世界に広がる不確実性を制御できる方法を開発し始めました。 最近のノーベル賞(Black-Scholesモデル、VaRなどで受賞)は、経済プロセスの数学的モデリング、市場の動きを予測し、その安定性を評価しようとする傾向を明らかに示しています。
今日は、最も広く使用されている損失予測の方法であるバリューアットリスク(VaR)についてお話します。
VaRコンセプト
エコノミストが理解できるVaRの説明は、次のとおりです。 本質的に、VaRは、何らかの不利な事象が発生した場合の、一定期間にわたる投資ポートフォリオの損失の価値です。 「好ましくない出来事」は、市場に影響を与える可能性のあるさまざまな危機、予測不可能な要因(法律の変更、自然災害など)として理解できます。 期間として、通常、1日、5日、または10日を選択します。これは、長期間にわたって市場の行動を予測することが非常に難しいためです。 許容可能なリスクのレベル(実際には信頼区間)は、95%または99%に等しくなります。 もちろん、損失を測定する通貨は固定されています。
値を計算するとき、市場は「通常の」方法で動作すると想定されます。 グラフィカルに、この値は次のように説明できます。
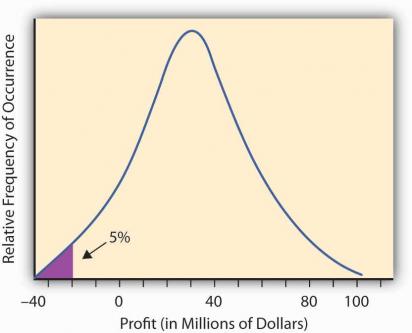
VaRの計算方法
VaRの計算に最も一般的に使用される方法と、その長所と短所を検討してください。
歴史的モデリング
歴史的モデリングでは、過去の測定から既知であるポートフォリオの財務変動の値を使用します。 たとえば、過去200日間のポートフォリオの振る舞いがあり、それに基づいてVaRの計算を決定します。 翌日、金融ポートフォリオが前日のいずれかと同じように動作するとします。 したがって、翌日には200の結果が得られます。 さらに、この事実に基づいて、確率変数が正規の法則に従って分布すると仮定し、VaRは正規分布のパーセンタイルの1つであることを理解します。 許容可能なリスクのレベルに応じて、適切なパーセンタイルを選択し、その結果、関心のある値を取得します。
この方法の欠点は、ポートフォリオに関する予測を構築できないことです。これについては情報がありません。 ポートフォリオの構成要素が短期間で大幅に変化する場合にも問題が発生する可能性があります。
コンピューティングの良い例は、次のリンクで見つけることができます。
リーディングコンポーネントメソッド
各金融ポートフォリオについて、資産の可能性を評価するのに役立つ一連の特性を計算できます。 これらの特性はリードコンポーネントと呼ばれ、通常、ポートフォリオの価格の偏微分のセットです。 ポートフォリオの価値を計算するために、通常はブラックショールズモデルが使用されます。これについては次に説明します。 一言で言えば、このモデルは、ヨーロッパのオプションの評価が時間とその現在の値に依存することを表しています。 モデルの動作に基づいて、数学的分析の古典的な方法(凸/凹、増加/減少の間隔など)を使用して関数を分析することにより、オプションの可能性を評価できます。 分析データに基づいて、各コンポーネントのVaRが計算され、結果の値は各推定値の組み合わせ(通常は加重合計)として構築されます。
モンテカルロ法
モンテカルロ法は多くの点で歴史的モデリング法に似ていますが、違いは計算が実際のデータではなく、ランダムに生成された値に基づいていることです。 この方法の利点は、多数の状況を考慮し、極端な条件での市場行動をエミュレートできることです。 明らかな欠点は、このアプローチを実装するために必要な大きな計算リソースです。 この手法を使用する場合、通常、NoSQLリポジトリとMapReduceに基づく分散計算が使用されます。 Hadoopを使用してVaRを計算する良い例は、 次のリンクにあります。
当然、これらはVaR計算方法だけではありません。 価格予測には単純な線形モデルと二次モデルの両方があり、変動共分散のかなり複雑な方法もありますが、これについては説明しませんでしたが、興味のある方は以下の本で方法の説明を見つけることができます。
テクニックに対する批判
VaRを計算する際、通常の市場行動の仮説が受け入れられることに注意することが重要です。ただし、この仮定が真である場合、7000年に1回危機が発生しますが、これは絶対に真実ではありません。 著名なトレーダーで数学者のナッシム・タレブは、「Fooled by Chance」と「The Black Swan」の本で、既存のリスク評価システムを批判し、対数正規分布に基づく別のリスク計算システムを使用するという形でソリューションを提供しています。
批判にもかかわらず、VaRはすべての主要な金融機関で非常にうまく使用されています。 このアプローチは常に適用できるとは限らないことに注意してください。そのため、他のメソッドは同様のアイデアで作成されましたが、異なる計算メソッド(SVAなど)で作成されました。
批判を考慮して、VaRの修正は、ガウス曲線のピークにおける他の分布または他の計算方法に基づいて開発されました。 しかし、私はそれについてもう一度話をしようとします。
参照資料
このトピックに関する興味深い本:
