3次元関数のグリッドグラフと等値線を描画する

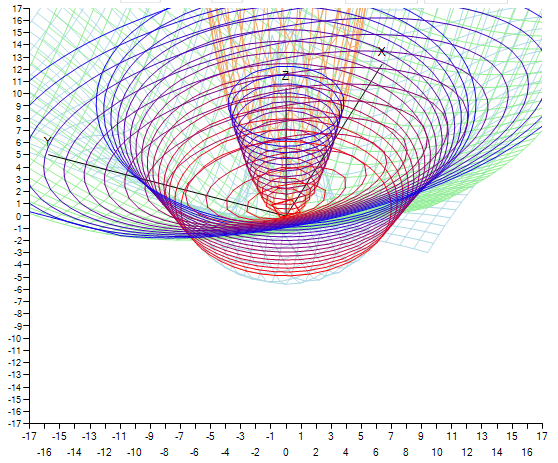
この記事は、C =での実装例を使用して、z = f（x、y）の形式の関数の非常に興味深い3次元グラフを構築するための一種の「実践ガイド」です。



もちろん、 Chartコンポーネントに描画します。もちろん、キャンバスのような要素を使用できます。 多数のポイントがある場合、描画の遅延が観察されますが、このコンポーネントは使いやすく、デモンストレーションに非常に適しています。

チャートを作成する

これを行うには、グリッドまたはフィールドが必要です。各ノードには、x、y座標があり、値zが含まれます。 このグリッドは任意の方法で塗りつぶすことができます。関数をプロットしているため、この関数の値（z = f（x、y））で塗りつぶします。 xまたはyの2つの連続する値の間のステップは1に選択されます。より簡単で視覚的なデモンストレーションのために、グリッドディメンションはN x Nです。グリッドノードの値は一度カウントするのに十分です。 3次元座標を2次元に変換し、グラフを回転させるには、回転行列とオイラー角を使用します。



角度α、β、およびγをそれぞれ角度a、b、およびcで表し、それらの値を度単位で使用します。 係数を使って行列を書きます：

    |  l1、l2、l3 |	
  M = |  m1、m2、m3 |
    |  n1、n2、n3 |
 l1 = cos（a）* cos（c）-cos（b）* sin（a）* sin（c）      
 m1 = sin（a）* cos（c）+ cos（b）* cos（a）* sin（c）       
 n1 = sin（b）* sin（c）       
 l2 = -cos（a）* sin（c）+ cos（b）* sin（a）* cos（c）        
 m2 = -sin（a）* sin（c）+ cos（b）* cos（a）* cos（c）      
 n2 = sin（b）* cos（c）
 l3 = sin（b）* sin（a）
 m3 = -sin（b）* cos（a）       
 n3 = cos（b）

3次元座標から2次元座標への最終的な変換を記述します。

X = l ₁ x + l ₂ y + l ₃ z

Y = m ₁ x + m ₂ y + m ₃ z

x、y、zはグラフの「内部」座標、X、Yは画面全体の座標です。 係数n1、n2、およびn3は、このタスクには必要ありません。

double[,] a; //  N x N … double X, Y; //      x for (int x = 0; x < N; x++) { for (int y = 0; y < N; y++) { X = l1() * (x - N / 2.0) + l2() * (y - N / 2.0) + l3() * a[x, y]; Y = m1() * (x - N / 2.0) + m2() * (y - N / 2.0) + m3() * a[x, y]; chart1.Series[n].Points.AddXY(X, Y); } n++; } //      y for (int y = 0; y < N; y++) { for (int x = 0; x < N; x++) { X = l1() * (x - N / 2.0) + l2() * (y - N / 2.0) + l3() * a[x, y]; Y = m1() * (x - N / 2.0) + m2() * (y - N / 2.0) + m3() * a[x, y]; chart1.Series[n].Points.AddXY(X, Y); } n++; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

角度が変わり、グラフが回転するイベントを追加します。 たとえば、これはマウスの左ボタンを押したままのカーソルの移動と、角度bとcの変更です。

 bool onmove = false; Point startpos; … private void chart1_MouseDown(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left) { onmove = true; startpos = e.Location; } } private void chart1_MouseMove(object sender, MouseEventArgs e) { if (onmove) { if ((startpos.Y - eY) < 0) b--; if ((startpos.Y - eY) > 0) b++; if ((startpos.X - eX) < 0) c--; if ((startpos.X - eX) > 0) c++; if (b > 359) b = 0; if (c > 359) c = 0; if (b < 0) b = 359; if (c < 0) c = 359; drawscene(); } } private void chart1_MouseUp(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left) onmove = false; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

テスト関数z = x ² + y ^{2を確認し}ます。



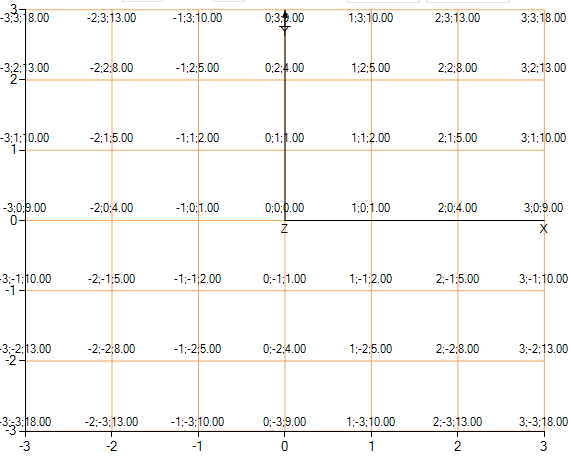
グリッドが表示され、ノードの値が表示される関数の上面図。



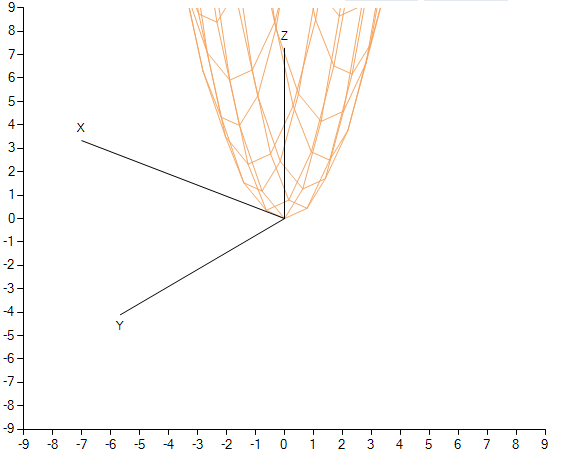
関数の視野角。

3つの角度すべてを使用して回転し、1未満のピッチのグリッドを使用して、角度を別の方法で変更する価値があるかもしれませんが、状況を単純化しました。

建物の輪郭

「マーチングスクエア」アルゴリズムを使用します。かなり詳細な説明はウィキペディアに記載されています。 Googleは、このアルゴリズムについて説明し、C＃で実装する非常に優れた記事も提供しています。

一番下の行は次のとおりです。

1.開始位置を見つける必要があります-輪郭の出所です。

2.次に、頂点と正方形を形成する隣接グリッドノードの値を比較します：（x _i 、y _j ）、（x _i-1 、y _j ）、（x _i 、y _j-1 ）、（x _i-1 、 y _j-1 ）。



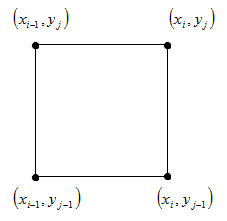
3.手順2で取得した値に応じて、バイパスのさらなる方向を選択し、手順2を繰り返す次のポイントに進みます。

4.開始位置に戻るか、グリッドの端に到達するまで実行します。

合計で16のオプションがあります。



すべてのコードを再度書くのではなく、 その記事のコードの一部を取り、タスクに合わせて変更します。

 enum dir { None, Up, Left, Down, Right } dir prevStep; dir nextStep; bool border; int startx, starty; void findstartpos() { for (int y = 0; y < N; y++) for (int x = 0; x < N; x++) if (arr[x, y] < Z) { startx = x; starty = y; return; } } bool check(int x, int y) { if (x == N - 1 || y == N - 1 || x == 0 || y == 0) border = true; if (x < 0 || y < 0 || x >= N || y >= N) return false; if (arr[x, y] < Z) return true; return false; } void step(int x, int y) { bool ul = check(x - 1, y - 1); bool ur = check(x, y - 1); bool dl = check(x - 1, y); bool dr = check(x, y); prevStep = nextStep; int state = 0; if (ul) state |= 1; if (ur) state |= 2; if (dl) state |= 4; if (dr) state |= 8; switch (state) { case 1: nextStep = dir.Down; break; case 2: nextStep = dir.Right; break; case 3: nextStep = dir.Right; break; case 4: nextStep = dir.Left; break; case 5: nextStep = dir.Down; break; case 6: if (prevStep == dir.Down) { nextStep = dir.Left; } else { nextStep = dir.Right; } break; case 7: nextStep = dir.Right; break; case 8: nextStep = dir.Up; break; case 9: if (prevStep == dir.Right) { nextStep = dir.Down; } else { nextStep = dir.Up; } break; case 10: nextStep = dir.Up; break; case 11: nextStep = dir.Up; break; case 12: nextStep = dir.Left; break; case 13: nextStep = dir.Down; break; case 14: nextStep = dir.Left; break; default: nextStep = dir.None; break; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

テスト関数z = x ² + y ^2をもう一度試してみましょう。



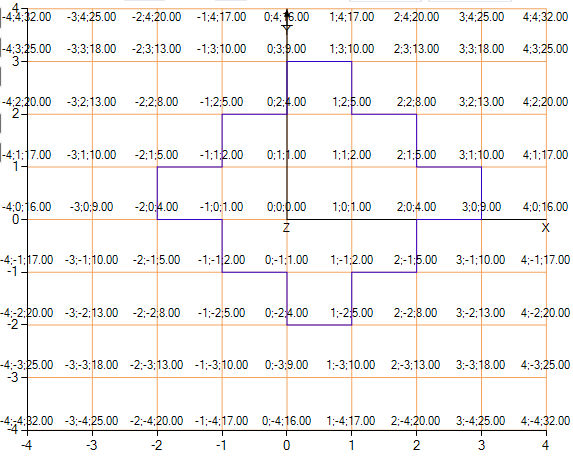
図からわかるように、アルゴリズムは非常にうまく対処し、関数値が5を超えているが、わずかに右側にあるポイントを分離しています。 輪郭は角張っていることが判明したため、補間します。 補間の意味は、グリッドの隣接ノードのzの値に基づいて、実際の輪郭に近いxまたはyの値を計算することです。これにより、輪郭がより妥当になります。

線形補間式を使用します。

x =（Zf（x _i-1 、y _j ）/（f（x _i 、y _j ）-f（x _i-1 、y _j ））+ x _i-1 、

y =（Zf（x _i 、y _j-1 ）/（f（x _i 、y _j ）-f（x _i 、y _j-1 ））+ y _j-1 、

ここで、Zは分離する値です。

前のステップと次のステップの動きの方向に応じて、x座標またはy座標に沿った補間が選択されます。

このようなあまり良くないコードを書いてみましょう：

 ... List<PointF> res; ... //  x  y int dx = 0, dy = 0; switch (prevStep) { case dir.Down: dy = 1; break; case dir.Left: dx = 1;break; case dir.Up: dy = -1; break; case dir.Right: dx = -1; break; default: break; } ... double X = x0 + x; double Y = y0 + y; if (ip) //ip - interpolation { //    if (dx != 0 && prevStep == nextStep) Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1; if (dy != 0 && prevStep == nextStep) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; //    if (nextStep == dir.Down && prevStep == dir.Left) Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1; if (nextStep == dir.Left && prevStep == dir.Down) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; if (nextStep == dir.Up && prevStep == dir.Right) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; if (nextStep == dir.Up && prevStep == dir.Left) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; if (nextStep == dir.Right && prevStep == dir.Up) Y = y0 + y + (Z - a[x, y - 1]) / (a[x, y] - a[x, y - 1]) - 1; if (nextStep == dir.Right && prevStep == dir.Down) X = x0 + x + (Z - a[x - 1, y]) / (a[x, y] - a[x - 1, y]) - 1; // ""  if (!(nextStep == dir.Down && prevStep == dir.Right) && !(nextStep == dir.Left && prevStep == dir.Up)) res.Add(new PointF((float)X, (float)Y)); } ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、より快適な結果が得られます。





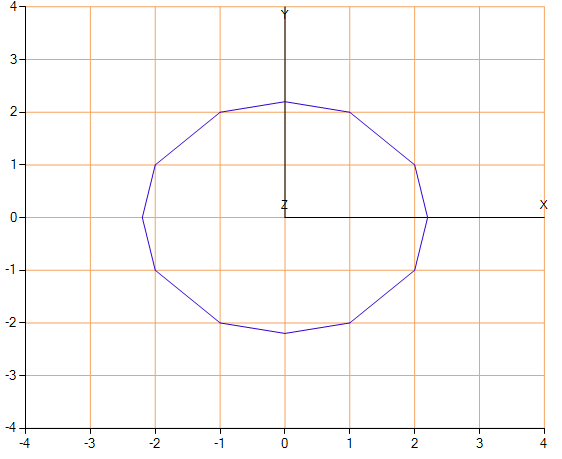
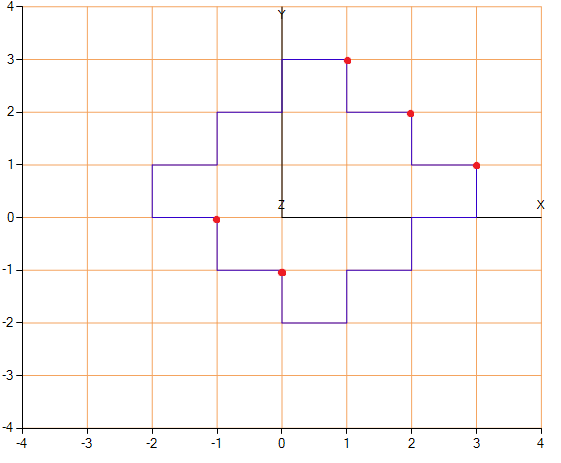
除外した「不要なポイント」の例。

可能な改善のうち、実装によって単調に増加する関数（減少する場合は符号を「>」に変更する）のみのすべての輪郭を作成することに注意してください。 定期的に増減する機能の場合、たとえば初期位置を見つけて数回実行する機能を変更する必要があります。



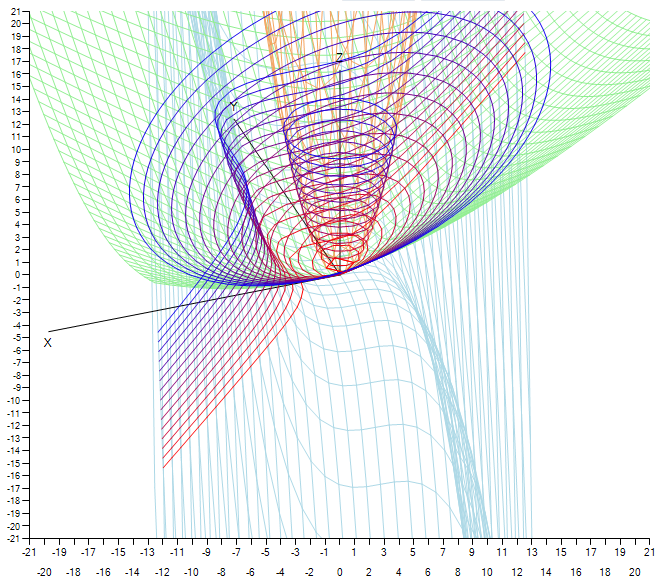
最終プログラムの作業の例。

実際には、これを使用してマップを分析したり、画像のアウトラインを検索したりできます。



プログラムのソースコードは、 こちらまたはこちらからダウンロードできます 。

もう一度、使用されたリンク：

en.wikipedia.org/wiki/Rotation Matrix

en.wikipedia.org/wiki/オイラーの角度

en.wikipedia.org/wiki/Interpolation

en.wikipedia.org/wiki/Marching_squares

devblog.phillipspiess.com/2010/02/23/better-know-an-algorithm-1-marching-squares