このトピックでは、実例での基数ツリーの使用について説明します。 基数ツリーまたは残差ツリーは、リーフノードに値を格納するという原則に基づいて形成されたデータ構造です。 中間ノードは有限値の要素です。 次の例のように、数字のビット、文字列の文字、または数字の数字を使用できます。 Radix Treeを使用した特定の圧縮アルゴリズムは、実際の埋め込みシステムで使用され、電話のファイアウォールパラメーターを格納します。
参照条件
ソースデータ。
電話帳、または単に連絡先リストがあるとします。 各連絡先と
関連する属性セット。 「電話ファイアウォール」プログラムの場合、これらはブール属性になります。
発信/着信コール、勤務中/勤務時間外の勤務、許可/ブロックまたは自動応答
呼び出すとき。 タスクは、カウンターポイントとその属性のリストを圧縮形式で電話メモリに保存することです。 使用可能なメモリが限られている場合。
したがって、より詳細な技術タスクは次のようになります。
-各番号の一連のルールを含む.INIファイルがあります。 ルールには電話番号が含まれています。
そして、それに適用される実際のブール属性。 部屋はユニークです。
.INIファイルの例（12345は電話番号）：
[ルール]
R0000 = 12345,0,0,0,0,0,0,0,0,0,0,0
R0001 = 123764465,0,0,0,0,0,1,0,1,0,0,0
...
R0765 = ...
-ルールの内部表現：
class NumberEntry
{
string number ;
bool attCalledNumber ;
bool attCallingNumber ;
bool attInboundCall ;
bool attOutboundCall ;
bool attWorkingHours ;
bool attNonWorkingHours ;
bool attBlocked ;
bool attAllowed ;
bool attPrefix ;
bool attAutoAnswer ;
};
* This source code was highlighted with Source Code Highlighter .
-既存のルールセットについては、中間の拡張グラフを作成する必要があります。
グラフでは、各ノードをリーフとしてマークできます。 たとえば、この一連の仮想番号を考えます。
012345
012346
01234567＃
54647
5463
54638
中間グラフを作成する必要があります。
図1. ToRからの拡張（圧縮されていない）グラフ。
-Advanced Graphは、次のルールに従って構築されます。
リストの各番号の最後の数字は、リーフノードを示します。 番号に関連付けられた属性は、リーフノードにのみ適用されます。 グラフでは、任意のノードをリーフとしてマークできます。 上記の例では、番号01234 5の番号5はリーフユニットを表しますが、番号01234 5 67＃の一部でもあります。
-すべての数値が中間列に追加された後（拡張）、圧縮する必要があります。 そのため、中間グラフのすべてのノード
（たとえば、0xxx5xxx＃）、一連のコンパクトノード（コンパクトノード、「x」なし）に置き換えられます。
拡張されたコンパクトなグラフのノードは、次の構造で表されます。
#pragma pack(push, 1) // 1 MS C++
#define K_MAX_EXPANDED_NODES 12 // . 0-9, * #
struct SG_Y_DigitElement // , 4
{
UINT digit : 4; // 0-9 . '*' 0xA, '#' 0xB. 12 , 4
UINT nextNodeOffset : 13; // ,
BOOL leafNode : 1; // ?
BOOL attCalledNumber : 1; // .
BOOL attCallingNumber : 1;
BOOL attInboundCall : 1;
BOOL attOutboundCall : 1;
BOOL attWorkingHours : 1;
BOOL attNonWorkingHours : 1;
BOOL attBlocked : 1;
BOOL attAllowed : 1;
BOOL attPrefix : 1;
BOOL attAutoAnswer : 1;
BOOL attReserved1 : 1;
BOOL attReserved2 : 1;
BOOL attReserved3 : 1;
BOOL attReserved4 : 1;
}
typedef SG_Y_DigitElement SG_Y_ExpandedNode[K_MAX_EXPANDED_NODES];
struct SG_Y_CompactNode // 5 . +
{
UINT8 nodeLen : 4;
UINT8 reserved : 4;
/* */
SG_Y_DigitElement digits;
} ;
#pragma pack(pop)
* This source code was highlighted with Source Code Highlighter .
-SG_Y_ExpandedNode型の要素の配列で表される拡張グラフに基づいて、SG_Y_CompactNode型のノードを持つコンパクトなグラフが構築されます。 したがって、SG_Y_ExpandedNodeから「x」として指定された空の要素を削除することにより、データが圧縮されます。 上記の例の拡張グラフの場合、圧縮後のコンパクトグラフは次のようになります（緑はコンパクトノードの桁数、SG_Y_CompactNode構造体のnodeLenフィールドを示します）。
図2. TKの圧縮グラフ。
-両方の列のノード（SG_Y_DigitElementのnextNodeOffsetフィールド）へのポインターは、グラフの最初のバイトに対するインデックスを表すことに注意してください。 両方のグラフは配列で表されます。
-TORを要約するには：
- 電話番号のファイアウォールルールを含む.INIファイルが受信されます。
- タイプNumberEntryのリストにルールを読み込む
- リストに基づいて中間の拡張グラフを作成します。 グラフのリーフノードには、番号に関連する属性が含まれます。
- 拡張から空の要素を削除して圧縮グラフを生成します
中間グラフの作成
アルゴリズムの最初のステップは簡単です。 ルールが読み取られ、リストに追加されると想定しています。 リストには一連の数値があり、グラフジェネレーターへの入力です。 ここおよび添付のソースでは、グラフジェネレーター（GraphGenerator）という用語を使用して、構築および圧縮アルゴリズムを実装するクラスを示しています。
中間拡張グラフ（拡張）の構築に直接進みます。
再び図1に注目してください。この中間グラフは、Radix Treeの原理に基づいて構築されたバイナリツリーとして表すことができます（またはロシア語の類似物は残基のツリーです）。 このデータ構造を詳しく見てみましょう。
基数ツリーへの要素の追加は次のとおりです。
-追加された値のi番目のビットごとに取得されます。
-要素は、現在のビットに基づいてツリーにプッシュされます。 i番目のビットが0の場合、左に進み、そうでない場合は右に進みます。
同様に、値のすべての重要なビットが処理されるまで続きます。
-結果として、基数ツリーリーフノードは値自体を示します。 したがって、ルートからリーフノードに移動すると、
値のすべてのビットを取得します。 アプローチの実例はここにあります 。 ロシアのウィキにはまだ基数ツリーの説明がありません。
たとえば、0123、01234、123の 3つの数字を使用します。 その後、最初の反復で、ツリーが上から下に構築され、4つのノード（0,1,2,3-leaf）が作成されます。 2番目の反復で、番号01234を追加するとき、要素0、1、2、および3を追加するときと同じパスに従います。これらの番号のノードは既に作成されているためです。 しかし、値3のノードにある最後の要素を追加するとき、新しいリーフノード4を作成します。3回目の反復で、番号123の追加が右側に発生します。
結果のツリーをグラフの形式で表す場合、右側のノードは「兄弟」、左側のノードは「息子」である場合、次の図が得られます
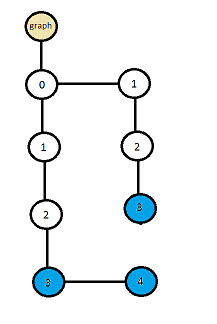
図3.グラフの関係
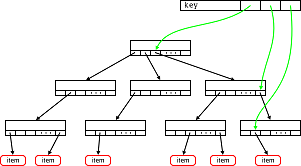
拡張グラフの基数ツリーに追加するアルゴリズムを適用します。 グラフノードは、12個の可能な値（0〜9 *＃）の配列で表されます。 つまり、expandedNode [digit]マッピングを使用して、ノードの値を確認および設定します。
次の図では、expandedGraphはexpandedNodeノードの配列として表されています。 「-」は空の要素、青の要素はリーフノードを示します。 問題のリーフノードには数値の属性が含まれていることを思い出させてください。
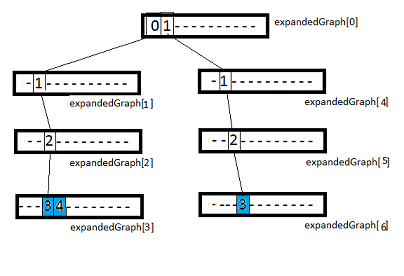
図4.拡張（非圧縮）グラフ
Radix Treeを使用するという考え方は既に明確になっており、空の要素を削除することで圧縮できることは明らかです。
圧縮 コンパクトなグラフの構築。
圧縮アルゴリズムは比較的単純で、2つの文で説明できます。 展開されたグラフexpandedGraphがあり、expandedNodeの配列として表示されます。
-expandGraph [i]ノードから空でない要素（数値）を取得します。 SG_Y_CompactNodeの配列で表される圧縮グラフにそれらを転送します。 コンパクトユニットの長さを空でない要素の数として設定します。
-各子ノードに圧縮手順を適用します。 CompactGraphの開始に関する子要素への参照を変更します。
圧縮アルゴリズムは再帰的です。 ノードから空でない要素を選択し、ノードの長さを設定して、それらを圧縮グラフに順番に配置します。 したがって、拡張ビューノードから
「01 -----------」、コンパクトノード '[2] 01'を取得します。[2]はノードの長さです。
子要素 '0'および '1'のプロシージャを再帰的に呼び出します。 次に、圧縮されたグラフの先頭に関連する子に「0」と「1」を関連付けます。
図5.結果は圧縮されたグラフです。
おわりに
-電話番号の圧縮と保存には、アルゴリズムの使用が最適です。 携帯電話会社のコード 、国コード 、都市コードなどのプレフィックスを使用すると、これらの同じコードをグラフのルートノードに保存できます。 実装は、大規模な通信会社のソフトウェアで直接使用されます。
ただし、任意のデータシーケンスに使用できます。 たとえば、大文字と小文字を区別するラテン文字データを保存するには、グラフノードのサイズを26要素に増やす必要があります。 したがって、数字フィールドの下で、5ビットを選択します。
属性が不要な場合は、SG_Y_DigitElementのサイズを最大2バイトに減らすことができます。 たとえば、文字値に5ビット、次のノードへのポインタに10ビット、シートマーカーに1ビット。
明らかに、アドレス可能なエントリの数の制限はnextNodeOffsetフィールドによって制限されます。 この例では、8192レコードをアドレス指定するには13ビットで十分です。
これがアルゴリズムの実装です