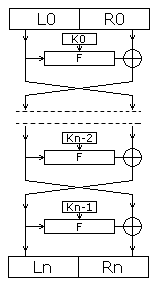
フグに関する記事の続きで、その基礎であるFeistelネットワークについてお話したいと思います 。 「主題の」人々はそれについて百回以上聞いた-このネットワークはブロック暗号の大部分で使用されています。 しかし、ここであなたは、正直なところ、右の写真から明らかなことはありますか? さて、一方通行(暗号化)は理解できるとしましょうが、逆も同様ですか?
そうでない場合は、マットの下にください
始めるには、少なくとも簡単にウィキステークを回って、それが何であるかを一般的な用語で理解してください
簡単にするために、2バイトのみで構成されるブロックを使用します。 ウィキペディアが言うように、あなたはそれを半分に切り、左側にL 、右側にRと名前を付ける必要があります。 だからそれ。
そして、ブロックの半分が2つあり、神秘的な関数Fがあります。
- 最初に学習する必要があるのは、 XOR (byで示される)は複雑な操作であるということです。 キックしないでください。1つの数字を別の数字と2倍にすると、再び目的の数字が得られます。 つまり A⊕B⊕B == A.
したがって、無限チェーンA⊕B⊕C⊕D⊕を構築することが可能です...そして、すべてを逆の順序で再描画すると、A
たとえば、((100⊕200)⊕50)⊕150 =8。したがって、8⊕150⊕50⊕200 = 100 - 2番目の重要な点は、ある時点ではブロックの半分のみが変化することです。
- 「ブラックボックス」または関数Fについて。原則として、関数Fは、すべての逆関数(復号化)で常に2番目の引数を持つため、発明された任意の関数(少なくとも愚かでは0を返す複雑なハッシュではあります)この関数の結果は、暗号化プロセス中と同じになります。 実際には、その作成はアートに似ており、暗号解読の新しい方法に対する100%の保証を提供しません。
この「同じ」はどのようにして生じるのでしょうか?
段階的な3ラウンドの例を考えてみましょう
暗号化
0) LとRにいくつかの数字があります。それらを100と200にします。Fは 、Lとラウンド数nに依存する関数です。 たとえば、Fで256を法として単純に追加します(バイトをクロールしないようにします)。 つまり F(L、n)=(L + n)%256。(%は除算の残り)
ラウンド1(n = 1)
1)R(200)を取り、関数F(L、n)の結果でXorimします。 200⊕((100 + 1)%256) 173を取得します。
2)Lの代わりに173を置き、Rの代わりにLの前の値(100)を置きます。 RとXor Rの結果を関数Fと入れ替えます。
ラウンド2(n = 2)
1)L = 173、R =100。Xorim100 s((173 + 2)%256)、 203
2)Lの代わりに203を、Rの代わりに173を置きます。
ラウンド3(n = 3)
1)L = 203、R =173。Xorim173 s((203 + 3)%256)、 99
2)最後のラウンド以降、Rのみを変更します(そのため、順列は行われません)。
暗号化後、L = 203、R = 99。
解読
私たちは逆の順序で進み、ラウンド数は3から1になります
ラウンド1(n = 3)
1)L = 203、R =99。Xorim99秒((203 + 3)%256) 173を取得します。 おなじみの番号?
2)Lの代わりに173、Rの代わりに203
ラウンド2(n = 2)
1)L = 173、R =203。したがって、203⊕((173 + 2)%256)= 100です。 もうほとんど!
2)変更L = 100、R = 173
ラウンド3(n = 1)
1)L = 100、R =173。R(暗号化の場合のように置換は不要)= 173⊕((100 + 1)%256)= 200 URAAAA !!!
L = 100、R =200。薬局のように)
つまり、Feistelネットワーク全体は、 ブロックの両方の半分を、暗号化中に逆の順序で置き換えられたいくつかの計算値で交互にブロック するようになります。
最後に、上記のアルゴリズムを実装するJavaコード。
パブリック クラス BlockTest
{
private static int rounds = 3;
public void feist( int [] a、ブール反転)
{
int round = reverse? ラウンド:1;
int l = a [0];
int r = a [1];
for ( int i = 0; i <rounds; i ++)
{
if (i <rounds-1) //最後のラウンドでない場合
{
int t = l;
l = r ^ f(l、ラウンド);
r = t;
}
その他 //最終ラウンド
{
r = r ^ f(l、ラウンド);
}
ラウンド+ =逆方向? -1:1;
}
a [0] = l;
a [1] = r;
}
private int f( int b、 int k)
{
return b + k;
}
公開 ボイドテスト()
{
int [] a = new int [2];
[0] = 100;
[1] = 200;
feist(a、 false );
feist(a、 true );
}
}
楽しんでいただけたでしょうか;)