正直なところ、Rosenblattの収束定理を参照することはできましたが、「Googleに送信された」ときは気に入らないので、理解しましょう。 しかし、Rosenblattパーセプトロンが何であるかをオリジナルから知っているという事実から理解します(理解の問題は表面化しましたが、私はまだ個人のみがそれを持っていることを望みます)。
材料から始めましょう
そのため、最初に知っておく必要があるのは、パーセプトロンのAマトリックスとパーセプトロンのGマトリックスです。 ウィキペディアへのリンクを提供し、信頼できるように自分で書きました(元から直接):
1. パーセプトロンのA行列
2. パーセプトロンのGマトリックス 、ここではパーセプトロンの AとG-マトリックスの関係に注意を払う必要があります。
これをマスターしていない人は、これ以上読んで、記事を閉じて喫煙しないでください-この記事はあなたのためではありません。 急いではいけません、人生のすべてが一度に明らかになるわけではなく、パーセプトロンのニュアンスを研究するのにも数年かかりました。 ここで少し読んでください-実験をしてください。
次に、パーセプトロンの収束の理論について話しましょう。 彼らは彼女についてたくさん話していますが、私は50%が彼女を目にしていないと確信しています。
だから、私の科学記事の1つから:
次の定理が証明されました。
"''定理3. ''基本パーセプトロン、刺激空間W、およびいくつかの分類C(W)が与えられた場合。 それから解の存在のために、C(W)と同じオーシャントにあるベクトルuと、Gx = uとなるようなベクトルxが存在することが必要かつ十分です。
この定理からの2つの直接的な帰結:
「 ''帰結1. ''初等パーセプトロンと刺激空間Wが与えられます。そして、Gが特異行列(行列式がゼロ)である場合、解のない分類C(W)があります。
「」「系2」「空間Wの刺激の数が要素パーセプトロンの要素の数Aより大きい場合、解決策がない分類C(W)があります。」
Rosenblattは、刺激空間をソースデータ空間と呼びます。
私は自然に証拠を考慮しません(元を参照)が、次に重要なことは、パーセプトロンの収束が数学的に保証されないことです(保証されないことを意味するわけではありません-単純な入力データでは、たとえ違反されても、任意の入力データについて話します) 2つの場合:
1.トレーニングセットの例の数が中間層のニューロンの数(A要素)より大きい場合
2.行列Gの行列式がゼロの場合
最初の部分では、すべてが単純です。A要素の数は、トレーニングセットの例の数に常に等しく設定できます。
そして、ここで、2番目の部分は、私たちの質問に照らして特に興味深いものです。 Gマトリックスの種類の理解を習得した場合、それは入力データと、最初のレイヤーで偶然に形成された接続の種類に依存することは明らかです。
そして今、私たちは質問に行きます:
しかし、パーセプトロンの結合の最初の層はランダムに選択され、訓練されていないため、パーセプトロンは等確率で線形に分離できない入力データで動作する場合と動作しない場合があり、線形入力データのみが完全な動作を保証すると考えられています。 言い換えれば、-等しい確率のパーセプトロン行列は、特別である場合も特別でない場合もあります。 ここでは、そのような意見が間違っていることが示されます。 (以下、私の科学記事からの引用)
A-要素の活動の確率
マトリックスAの定義から、それはバイナリであり、対応するA-要素がアクティブな場合に値1をとることがわかります。 行列にユニットが現れる確率と、それに応じてゼロになる確率に興味があります。
次に、詳細を少しスキップして、すぐに写真を示します。
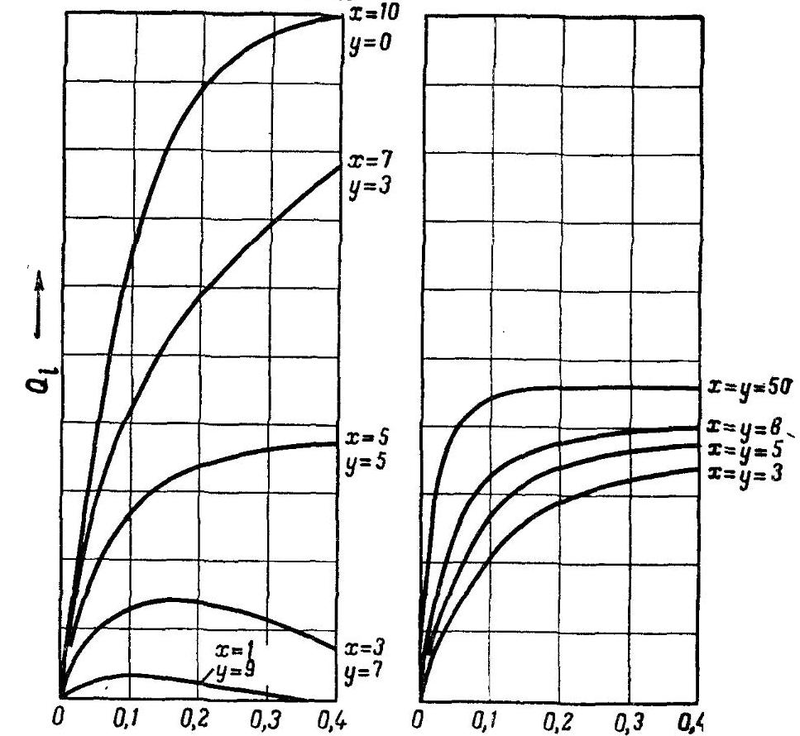
これはいわゆる Rosenblattによって分析されたQ関数。 詳細は説明しませんが、ここでは次のことが重要です。
xは、1つのA要素(重み+1)に一致する最初の層の励起結合の数であり、 yは抑制結合(重み-1)の数です。 図のY軸は、このQ関数の大きさを示しています。これは、網膜上の入力された要素の相対数(入力で1)に依存します。
この図は、網膜の照明領域の大きさに対するA-要素Qiの活動確率の依存性を示しています。 励起された結合(y = 0)のみがあり、照射されたS-要素の数が多いモデルの場合、Qiの値は1に近づきます。つまり、A-要素の活動確率は、照射されたS-要素の数に直接依存しますが、これは悪いです比較的小さな画像と大きな画像の認識に影響します。 以下に示すように、これはA-行列が特別である可能性が高いためです。 したがって、幾何学的な寸法のパターン認識の安定性のために、A-要素の活動の可能性が照明されるS要素の数にできるだけ依存しないように、x:y比を選択する必要があります。
... x = yで、Qiの値は、非常に少数または非常に多数の照らされたS-要素を除いて、領域全体でほぼ一定のままであることがわかります。 また、債券の総数を増やすと、Qiが一定の領域が拡大します。 小さなしきい値でxとyに等しい場合、0.5に近づきます。 任意の刺激でA要素の活動が発生する可能性に等しい 。 したがって、行列Aのユニティとゼロの出現が等しく発生する条件が見つかります。
この場合、行列Aのユニット数は二項分布で記述されます。 たとえば、次の図は、サイズ5x5のマトリックス内のユニット数nに応じたマトリックス数Nの分布を示しています
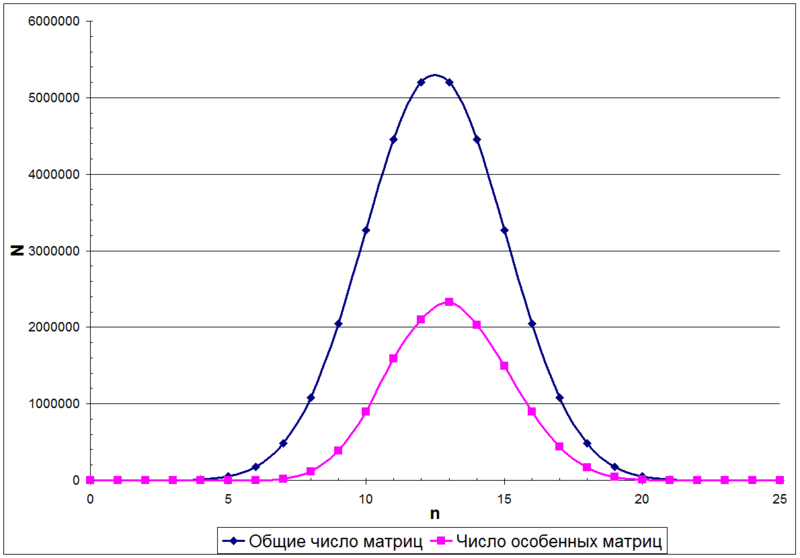
最後に、Aが特別である確率はどのくらいですか?
二項分布から、マトリックス内の異なる単位数を持つマトリックスの総数がどのように分布しているかを知ることができます(前の図の上の曲線)。 ただし、非特異行列の数(前の図の下部の曲線)については、数式は現在存在しません。
しかし、シーケンスA055165 [6]があります。これは、サイズnxnの行列が特別ではないという事実の確率を与えます。 ただし、徹底的な検索によってのみカウントでき、これはケースn <= 8の前に行われます。 しかし、モンテカルロ法を使用して後続の値を取得できます...
そして、これは次の図に見られるものです(これらは、サイズに応じて非特殊マトリックスが出現する確率です)。
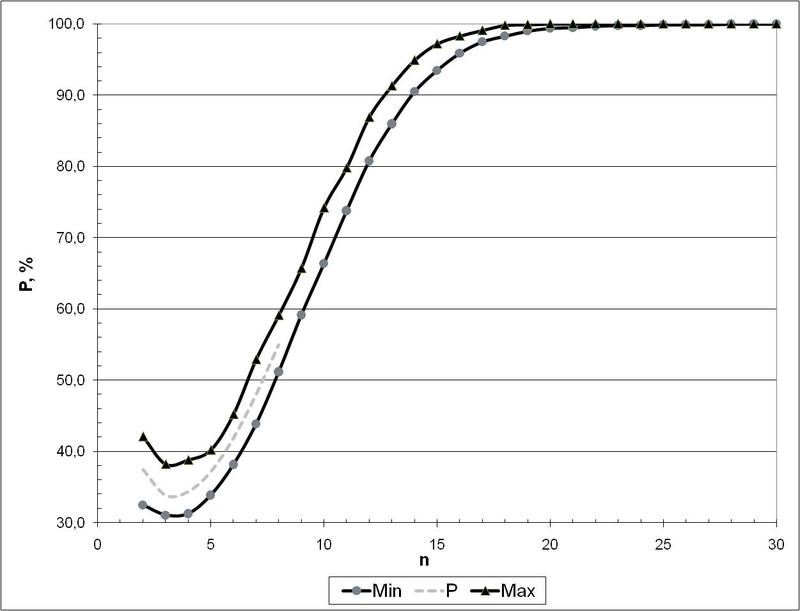
したがって、これから、マトリックスサイズが30 x 30(つまり、A要素の数が30以上の場合)であっても、ランダムに取得されたマトリックスが特別ではないというほぼ100%の確実性を語ることができます。 これは、ローゼンブラットパーセプトロンがコンパクト性仮説を満たす空間を形成する最終的な実用条件です。 実際には、G行列が特殊になる場合を除外するために、最低約100個のA要素を使用する方が信頼性が高くなります。
そして結論として。 今すぐ自問してください:MLP + BackPropは保証されていますか、Rosenblattパーセプトロンに関してここで説明したことは何ですか? 私はこれに関する説得力のある証拠をどこにも見つけませんでした(数学へのリンクを投げないでください。勾配降下の収束の証拠-これはこれに当てはまりません。このテーマに関して自分のわかりやすい記事を書くことをお勧めします:「 頭からの考えはHabrahabrで歓迎されます 」より建設的)。 しかし、BackPropを使用するときにローカルミニマムに入る問題に基づいて、Rosenblattパーセプトロンのように、すべてがきれいで滑らかではないようです。
更新しました。 プレゼンテーションでは多少見落としていましたが、対話中にここで明らかにしました。 先導的な質問をしてくれたretranとjustseregaに感謝します。
まとめ 結果1と2では、特定の条件下では解決が不可能であると言われています。 ここで、n> 30でそのような条件が発生しないことを証明しました(Rosenblattはこれを行いませんでした)。 しかし、読者には2つの質問がありました
1. さて、A行列(およびそれを介してG)は、高い確率で適切です。 しかし、これはどのように別のスペースに移動するのに役立ちますか? 。 実際、あまり明白ではありません。 説明します。 Aマトリックスは「その他の空間」、つまり標識の空間です。 行列が特別ではなく、この行列が元の次元よりも1次元大きいという事実は、線形に分割できることを示しています。 (これは、結果と定理3から続く)
2.「 Rosenblattパーセプトロンのエラー修正アルゴリズムが収束するという証拠はありますか? 」 確かに、定理3は、解決策が存在することのみを述べています。 これはすでに、このソリューションが属性のスペースに存在することを意味しています。 ランダムな最初のレイヤーを操作した後。 エラー修正アルゴリズムは第2層で教えられ、Rosenblattには定理4があり、既存の可能なソリューション(定理3も存在する)がエラー修正学習アルゴリズムを適用することで正確に達成できることを証明しています。
もう1つの重要な点は、Aマトリックスが一方で入力データに依存し、他方で接続のランダムマトリックスに依存するという事実から得られます。 より正確には、入力行列は、ランダム演算子(ランダムに形成された結合)を介して行列Aにマッピングされます。 繰り返されるサブシーケンスの発生率などのランダム性の尺度を導入すると(擬似ランダム性)、(1)それがまったくランダムではなく、いくつかのルールに従って構築された演算子(つまり、最初のレイヤーに参加する)の場合、Aを取得する確率が大幅に増加します-特殊行列(2)入力行列に、私たちが取得した疑似ランダム性を掛けた後、A行列に規則的な単位ではなく、単位のランダムな広がりがある場合(この条件をRと呼びます)、これは上記の記事で分析したとおりです。
ここで私はあなたに私のテストされたものを明らかにします。 結合を作成するときのランダム性の二項モデルの考え方(これは、A要素が取得され、S要素へのNの刺激的接続とMの抑制的接続がランダムに引き出される場合)により、条件Rを満たせば十分ですが、収束プロセスを高速化するには、マトリックスA.これを行う方法-暗号化は単に私たちに伝えます。 暗号とのこのような接続がここに描かれています。