前の記事で 、目的関数としてのエネルギーの評価を放棄する必要がある(または少なくとも適切である)理由を実証しました。 誰かが知らない場合、目的関数は、目標に近づいているかどうかを評価できるように発明した関数です。 RNAは「正しく」折りたたまれる。
エネルギーが代表的なターゲットではない場合、どこに移動するかをより安定的/明確に示すものは何ですか? 絶対に形式化された正確な目標がある場合、これはすでに問題を解決したことを意味します。 目的関数自体の形式化は、プロセスの完全な理解に過ぎません。
しかし、そのような贅沢はありません。 最初に、我々は仮説を立てざるを得ません。それはプロセスが従う法則であり、ある意味でこれを目的関数に反映します。
もう一度、目的関数としてのエネルギーについて-RNAのホームであるRossetaでは、そのようでした
スコア=(VDW * 3.0 + RG)+(RNA_BS + RNA_BP_W + RNA_BP_H + RNA_BP_S)+(RNA_NONB * 1.5 + RNA_O2ST + RNA_PHOS)+(RNA_AXIS * 0.2 + RNA_STAG * 0.5)
解読しません。 しかし、これがさまざまな現在の影響の寄与の一定の合計であることが重要です。 結果は算術的に意味のあるものです。 そして、それに応じて、私たちは不定形なものに移行しています。 誰もパラメーターで正確な係数を与えません、これまたはそのパラメーターが貢献するもの。 しかし、それらを計算することは不可能です-目的関数を構築しています。 推測も当てはまりません。 最初に試してみました-そして、私は大きな半分が単に深刻な貢献をするのではなく、間違った場所での計算を拒否するだけであることがわかりました。
したがって、最初はVDWのみを残しました-これは一種の一般化係数であり、実際には禁止された共有結合があるかどうかを示します(最初の記事で説明しました)。 そして、時間の経過とともに、単純にyes / noの回答に置き換えました。 他のパラメータが-時にはそれを上回った-結果として、.pdbファイルで交差が取得されましたが、そうではありません。
さらに、私は水素結合の形成のみに依存することを提案したことを覚えています。 それらが形成されると、距離と角度-それだけです。 RNAのどこにあるか-安定していることもわかっています。 (より正確には、これは今ではかなりよく予測されており、ニュアンスがあります-しかし)。
図では、実験のために取った1つのリボザイムの二次構造
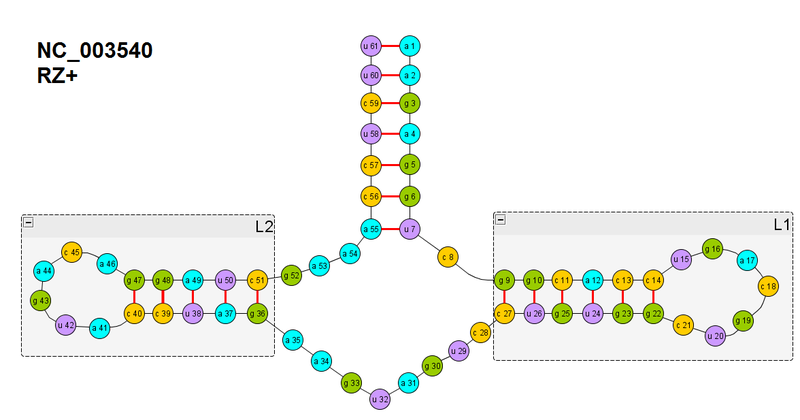
私の人生を単純化するために、私はRNA /タンパク質が階層的に折り畳まれるという既存の仮説から始めました:いわゆる 階層モデルには多くのバリエーションがありますが、本質は次のとおりです。 まず 、展開されたチェーンの二次構造の要素が形成され始めます 。 「開始」という言葉に焦点を当てると、これは完全に正常な仮説ですが、二次構造が完全に形成され、その後さらに折り畳まれることが理解される場合があります。 これはいくぶん間違っています。 しかし、これは後で、リボザイムを完全に折り畳むときに重要になります(すぐに言いますが、まだ成功していません-私の基準では、エネルギーに基づいていないので、彼らはより厳しいことが判明しました。しかし、私は解決策に近いようです)。
さて、少なくとも小さな部分を崩壊させて、2つのヌクレオチドの間に水素結合を形成しましょう。 cugacgucgの正しいループ(14から22)-9ヌクレオチドを取り、極端なcgの間に水素結合を形成します。
目的関数を作成する方法は?
cg間に3つの水素結合があるため、3つの距離(r1、r2、r3)と3つの角度(a1、a2、a3)があります。 関数が話すには、次のようにする必要があります。その値が最終的にゼロ以下の場合、3つの水素結合がすべて形成されています。 正の値は、この状態へのアプローチをスムーズに示す必要があります。
したがって、現在の距離から3オングストロームを減算し、角度から20度を減算する必要があります。 関数にプラスの貢献をする値を取得します。 これら3つの角度と3つの距離をすべて組み合わせて、目的関数の値を取得したいと思います。 しかし、距離と角度は軽くこじ開ける-異なる値。 したがって、1つのスケールにする方法があります。 重要な距離(3を引いた後)は1から12のどこかにあります。角度がこれらの距離に既に影響を与えているという意味で重要です。 また、距離が大きい場合、角度は重要ではありません。原子が深byで区切られている場合、原子の回転方法の違いは何ですか。 角度は0〜180、マイナス20 = 160です。
概算すると、距離に10を掛けると、距離と角度は同じスケールになります。 したがって、次のことを行います。
r1-= 3.0f; r1 * = 10;
r2-= 3.0f; r2 * = 10;
r3-= 3.0f; r3 * = 10;
a1-= 20;
a2-= 20;
a3-= 20;
2つのオプションがあります。 一
locScore =(r1 + r2 + r3 + a1 + a2 + a3)
そして第二
if(maxR> maxA)
{locScore = maxR; }
他に
{locScore = maxA; }
ここで、maxR =(r1、r2、r3)からの最大値、およびmaxA =(a1、a2、a3)からの最大値
オプションはそれぞれ独自の方法で優れています。 折りたたみを開始するには、2番目の方法が適しています。 すでに大まかな構造を作成した後、最初の構造が役立つ場合があります。
アルゴリズムは非常に単純です。番号付きのヌクレオチド(パートNo. 3-1500の可能なターンが選択されたことを思い出してください)を開始します
14
15
16
17
18-たとえば、ここでは番号210のターンがすべての中で最高です
19
20
21
22
たとえば、No。1とNo. 6の2つの角度(つまり、No。16)で回転します。 最適な修正を見つけます。 私たちの小さなチェーンは2つに折り畳まれます。 しばらくしてから、「張力」(左と右の端が接続する傾向があり、ループが張力を受ける)に入ると、回路は角度1と6で停止し、アルゴリズムはサイクルをたどります。 彼が最良の状態を与えなくなるとすぐに、例えば3と4(No. 34)などの角度の組み合わせを変更します。 これにより、角度1と6で電圧が徐々にアンロードされ、それでもそれらを「圧縮」することができます。
このアルゴリズムは、必要な水素結合を形成するのに十分です。
次の第2シーズンの記事では、スパイラル全体が形成されるときに生じる困難について説明します。 しかし、まだ1つのスパイラル。
PS深刻なコメントが3番目の記事に掲載されたことを非常に嬉しく思います。 しかし同時に、それは素人、潜在的なFoldItプレーヤー、または単にバイオをサポートしているように見えます。 分散コンピューティング-興味を失います。 一部を完了しました(こんにちは、RNA World)。 これ以上複雑になることはありませんが、おそらく残りの詳細は普通の人にとってそれほど興味深いものではありません(そうでない場合は書いてください)。 志を同じくする人や仮説をテストできる人を探していることを隠しませんが、同時に大量生産の準備ができておらず、ソフトウェアも準備ができていません。 一般的に、誰が気にかけて書いて、それから私はシーズン2のために速く熟します。
数学者にとって重要な質問 :
上記の2つの目的関数について説明しました
1.locScore =(r1 + r2 + r3 + a1 + a2 + a3)
2. if(maxR> maxA){locScore = maxR; } else {locScore = maxA; }
それらを1つにまとめる方法を知っていますか? つまり 最初の目的関数が5回使用され、2番目の目的関数が5回適用され、特定の結果(「エネルギー」の低下)が得られたとしましょう。 5回適用した後、結合後に取得した関数は、1番目と2番目を順番に適用した場合と同じ結果になることが必要です。 これは可能ですか?