注釈
この記事には、基準を真にランダムなシーケンスと一致させるためのランダムなシーケンスのグラフィカルなテスト方法の説明が含まれています。 この記事では、NISTテストパッケージに含まれる「近似エントロピー」法の概要を説明し、 Ocelotの記事「 マイクロコントローラーでの乱数生成」で説明されているPRNGを使用して取得したシーケンスの比較分析も提供します。
「近似エントロピー」のテスト
「近似エントロピー」の計算は、NISTテストスイートに含まれるテストの1つです。
このテストでは、ビットの初期シーケンス全体で、長さmビットのすべての可能な重複パターンの頻度をカウントします。 テストの目的は、長さmおよびm + 1の元のシーケンスの2つの連続するブロックのオーバーラップ周波数を、完全にランダムなシーケンスの類似ブロックのオーバーラップ周波数と比較することです。 テスト中に計算される確率pは少なくとも0.01でなければなりません。 それ以外の場合(p <0.01)、バイナリシーケンスは完全に任意ではありません。
ApEn(m)、ここでnは着信シーケンスのビット長です。 mは、テスト用の初期ブロックのビット単位の長さです。 εはビットシーケンスです
ステップ1
nビットシーケンスを完了して、mビットシーケンスと正確にn個のオーバーレイを取得します。 これを行うには、シーケンスの先頭から末尾にm-1ビットを追加します。
例:ε= 0100110101およびm = 3、次にn =10。シーケンスの先頭と末尾に0と1を追加します。 (これはmの各値に対して行われます)。
これにより、テストシーケンス010011010101が生成されます。
ステップ2
重複するn個のブロックの頻度が計算されます(たとえば、位置jでεjとεj + m-1を含むブロックが計算される場合、位置j + 1でεj + 1とεj + mを含むブロックが計算されます)。
可能なmビット((m + 1)ビット)値の数をC m iとして表します。ここで、iはmビット値です。
手順1で取得したテストシーケンスの場合、重複するmビットブロック(m = 3)は010、100、001、011、110、101、010、101、010、101になります。発生回数2 m = 2 3 = 8 mビットシーケンス:
#000 = 0、#001 = 1、#010 = 3、#011 = 1、#100 = 1、#101 = 3、#110 = 1、#111 = 0
ステップ3
iの各値に対してC m iを計算します。
C 3000 = 0、C 3 001 = 0.1、C 3 010 = 0.3、C 3 011 = 0.1、C 3 100 = 0.1、C 3 101 = 0.3、C 3 110 = 0.1、C 3 111 = 0
ステップ4
計算する
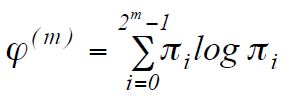 どこで
どこで
πi = C 3 jおよびj = log 2 i
現在の例:ϕ (3) = 0(log 0)+ 0.1(log 0.1)+ 0.3(log 0.3)+ 0.1(log 0.1)+
0.1(log 0.1)+ 0.3(log 0.3)+ 0.1(log 0.1)+ 0(log 0)= -1.64341772。
ステップ5
m = m + 1について手順1〜4を繰り返します。
ステップ6
値ApEn(m)=φ (m) -φ (m + 1)を取得します
現在の例では、ApEn(3)= -1.643418-(-1.834372)= 0.190954
着信値
次のように、nとmの値を選択する必要があります。m<log 2 n-5
プロット
グラフを取得するために、一連のテストを実行して、m = 2でApEnを計算しました。 nの値は、ステップ100で0から1,000,000の範囲で変化しました。一連のテストもステップ1で実行されました。ステップ1とステップ100で得られた結果には大きな違いはないため、テストはステップ100で正確に実行されました。 1,000,000ビットは、1つのスレッドでIntel Core i3 U380 1.33 GHzで約7分、16スレッドで約6:30分かかります。 対数スケールYはグラフの表示に使用され、結果は正規分布からの偏差として表示されます。 計算原理は、記事STEVEN M. PINCUSで説明されています。 システムの複雑さの尺度としての近似エントロピー
結果のグラフィック表示。
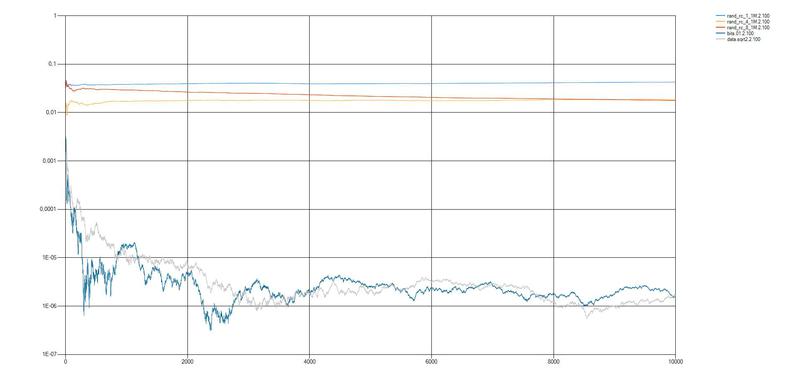
1.非同期タイマーのエントロピーのソース
タイマー1-ウォッチドッグ、RCジェネレーターからのクロック、周期T1 = 15 ms。
タイマー2-8ビット、水晶発振器からのクロック、クロック周波数F = 16.0 MHz。
rand_async_1_1M-カウンター2の最下位ビットが結果として使用されます生成レートは120ビット/秒
rand_async_4_1M-カウンター2の下位4ビットが結果として使用されます生成レート280ビット/ s
rand_async_8_1M-カウンター2の8ビットすべてが結果として使用される生成速度450ビット/ s

2. RC回路によるエントロピーのソース
時定数RC = 5ミリ秒。 クロックカウンター周波数F = 16.0 MHz。
rand_rc_1_1M-カウンターの最下位1ビットが結果として使用されます。 生成レート370 bps
rand_rc_4_1M-カウンターの下位4ビットが結果として使用されます。 1500ビット/秒の生成レート
rand_rc_8_1M-カウンターの8ビットすべてが結果として使用されます。 2870ビット/秒の生成レート
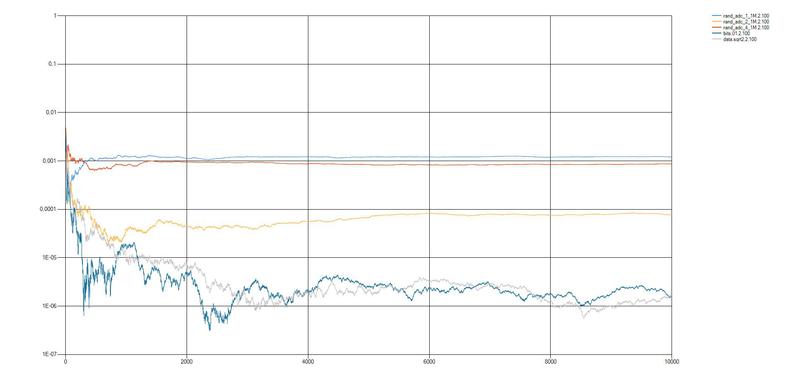
3. ADCのエントロピーのソース
測定された電圧はVDD = 3.3 V(安定化されていない)、基準電圧はVCC = 5.0 Vです。ADCの分解能は10ビットで、変換クロック周波数は125 kHzです。
rand_adc_1_1M-ADC結果の最下位ビットが結果として使用されます。 8.93 kbpsの生成速度
rand_adc_2_1M-ADC結果の下位2ビットが結果として使用されます。 生成レート17.9 kbps
rand_adc_4_1M-ADC結果の下位4ビットが結果として使用されます。 生成レート29.5 kbps
おわりに
結果のグラフ表示を見ると、マイクロコントローラーを使用して取得されたランダムシーケンスの品質は、 DIEHARDセットおよび数「2」から平方根を抽出して取得されたシーケンスのランダムシーケンスよりも数桁少ないと結論付けることができます。
最新の暗号化で取得したランダムシーケンスを使用することは非常に危険です。これは、NISTおよびDIEHARDテストの結果でも確認されています。 この研究の次のステップは、真にランダムなシーケンスを識別するために、一般的でない統計テストを使用することです。