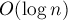Sqrt分解（ルート最適化）

Sqrt分解は、セグメントごとの量の計算などのオンライン操作を実行できるメソッドまたはデータ構造です。 およびアイテムの更新 。 フェンウィック ツリーやセグメントツリーなど、より効率的な構造があり、両方のリクエストで処理されます 。 ただし、ルートの最適化についてお話ししたいのは、 このメソッドには、異なるタイプのタスクに適用されるアイデアがあります。

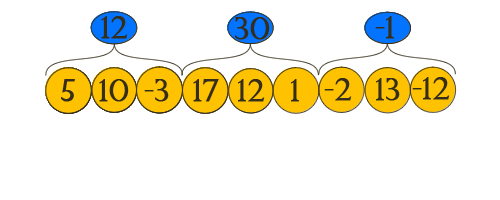
問題の声明

配列A [i]が与えられ、次の形式のリクエストが与えられます：

• セグメントの金額を計算[L; R]（後で、関数min、max、gcdなどを同様に計算できることを理解します。
• 要素A [i]に追加、デルタ

素朴な実装

つまり、部分量の配列を計算できます。

for(int j = 0; j < i; j++) B[j] += A[i];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

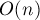そして、量の要求で[L; R]、B [R] -B [L-1]を返します 。 ただし、変更を要求すると、（この要素を含む）部分的な合計の再計算が必要になり、最悪の場合、順序の漸近を行います それは良くありません。

分解棟

主なアイデアは * = 。 つまり、もしあれば 要素、それからそれらすべてを分割することができます それぞれが長いブロック たぶん最後のものを除いて。 次に、すべてのブロックについて、その上の数値の合計を計算します。補助配列が占有することがすぐにわかります メモリ。

sqrtSums []配列の構築について説明します。

 int len = (int)sqrt(n) + 1; //  "sqrt-" int sqrtSums[MAXN], st = 0; //   for(int i = 0; i < n; i++) sqrtSums[i / len] += A[i];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

リクエストの説明

金額リクエスト（RSQ）

クエリの合計[L; R]、それに対する「迅速な」応答のために、すでに利用可能な情報を最大限に使用することが必要です。 すでに述べたように、サム[L; R] =合計[0、R]-合計[0; L-1]。 リクエストの処理方法Sum [0; R]。 最初のいくつかのセグメント([0; len-1], [len; 2*len-1], ...)



がクエリ[0;に完全に含まれることに注意してください。 R]、つまりsqrtSums[]



情報を使用できることを意味しsqrtSums[]



（ 、あるから ） ただし、次の形式の「尾」があります。 [k*len; k*len + delta]



[k*len; k*len + delta]



（delta <len、そうでない場合は別のセグメント[k*len; (k+1)*len-1]



を含めることができるため）、手動で計算できます（delta <len、漸近的に、 影響しません）。 以下に実装例を示します。

 int getPartSum(int r) { int it = 0, res = 0; while((it+1) * len -1 <= r) res += sqrtSums[it++]; //  ,   for(int i = it*len; i <=r; i++) res += A[i]; // "" return res; } int getSum(int l, int r) { if(l == 0) return getPartSum(r); else return getPartSum(r) - getPartSum(l-1); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

アイテム変更リクエスト

多くの構造では、このクエリを実装するには、ツリーをたどるか、ハッシュ関数などを計算する必要があります...ただし、ここでは2つの値のみを変更する必要があります（各要素は1つの「sqrtセグメント」に含まれます）

 int incElement(int index, int delta) { A[index] += delta; sqrtSums[index/len] += delta; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

範囲最小/最大/ Gcdクエリ

RMQクエリ（範囲最小/最大クエリ）に応答するには、合計とほぼ同じものが必要です。 ただし、「愚かな」アイテムを更新するには、 時間（要素を更新するとき、「sqrtセグメント」全体で最小/最大を再カウントします）が、更新に何らかの制限を課すと、推定値を達成します 。 つまり、最小値/最大値を見つける問題を解決するとき、要素の削減/増加のみを許可します。

最小値を更新するコード：

 int decElement(int index, unsigned int delta) //delta -     { A[index] -= delta; sqrtSums[index/len] = min(sqrtSums[index/len], A[index]); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

同様に、最大値を更新するには：

 int incElement(int index, unsigned int delta) //delta -     { A[index] += delta; sqrtSums[index/len] = max(sqrtSums[index/len], A[index]); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

RMQ問題では、タスクは[0; R]-[0; L-1]、つまり LからRまでの最小値/最大値を計算する必要があります（再度カウントしないで、[L; R]に完全に含まれる「sqrtセグメント」、漸近性が変化しない理由を考えてください。



GCD（Greatest Common Divisor）を計算するために、最小/最大で回した「チップ」を使用することはできません。 したがって、両方の操作は 。

GCDのコード（最小および最大の場合、getGCD関数はmin / maxに置き換えられます）：

 int getGCD(int a, int b) { while(a && b) { if(a < b) b %= a; else a %= b; } return a + b; } int gcdRQ(int l, int r) { int cur_gcd = A[l++]; for(int i = l; i <= r;) if (i % len == 0 && i + len - 1 <= r) { cur_gcd = getGCD(cur_gcd, b[i / len]); i += len; //  "sqrt-" } else cur_gcd = getGCD(cur_gcd, A[i++]); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ソース

つまり 、 このサイトを使用しました。

ハリコフのウィンターコンピュータースクールからの講義がこの記事に影響を与えたので、私はサイトを放り投げます。ビデオ講義を含む今年のコレクションがもうすぐ出るでしょう。



今のところ、それが明確であったことを願っています。