それはどうなるのでしょうか?
ラフ集合の理論は 、不確実性、不正確さ、不確実性を記述するための新しい数学的アプローチとして開発されました[ZdzisławPawlak、1982]。 これは、宇宙の各オブジェクトに何らかの情報(データ、知識)を関連付けるというステートメントに基づいています。 同じ情報によって特徴付けられるオブジェクトは、それらについて利用可能な情報の点で区別できません(類似)。 この方法で生成された識別不能な関係は、近似(ラフ)セットの理論の数学的基礎です。
近似集合の理論の概念の基礎は、集合の近似の操作です。
ここで、近似セットの近似の概念を示します。
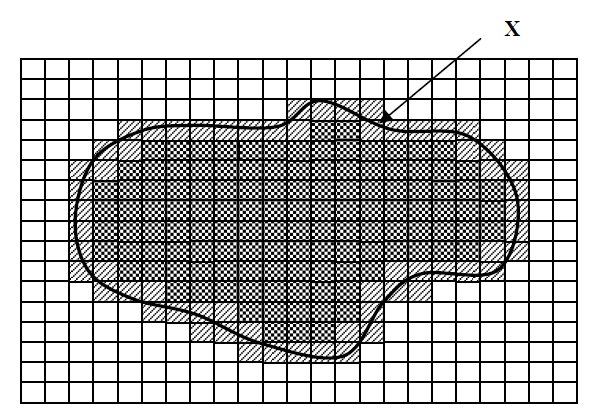
- セットXのより低い近似
 セットXに実際に属する要素が含まれます。
セットXに実際に属する要素が含まれます。 - セットXの上位近似
 +
+  おそらくセットXに属する要素が含まれます。
おそらくセットXに属する要素が含まれます。 - 境界 (上限と下限の近似値の差)
 区別できない領域です。
区別できない領域です。
実際のアプリケーション
近似セットは、属性値テーブル、情報システム、または決定テーブルとも呼ばれるデータテーブルを操作するときに使用されます。 決定表はトリプル=(U、C、D)です。ここで、
Uはたくさんのオブジェクトです
Cは条件属性のセットです
Dは決定属性のセットです。
表の例
| うん | C | D | |
| 頭痛 | 温度 | インフルエンザ | |
| U 1 | はい | 普通の | いや |
| U 2 | はい | 高い | はい |
| U 3 | はい | 普通の | いや |
| U 4 | はい | 非常に高い | いや |
| U 5 | いや | 高い | いや |
| U 6 | いや | 非常に高い | はい |
| U 7 | いや | 高い | はい |
| U 8 | いや | 非常に高い | はい |
テーブル分析
セット:
U = {U 1 、U 2 、U 3 、U 4 、U 5 、U 6 、U 7 、U 8 }
C = {頭痛、体温}
D = {Flu}
可能な属性値:
V 頭痛 = {はい、いいえ}
V 温度 = {標準、高、非常に高}
V インフルエンザ = {はい、いいえ}
頭痛属性の値に従ったセットUのパーティションは次のとおりです。
- S はい = {1、2、3、4}
- S no = {5、6、7、8}
- S = {{1、2、3、4}、{5、6、7、8}}
温度属性の値に応じたセットUのパーティションの形式は次のとおりです。
- S 通常 = {1、3}
- S high = {2、5、7}
- Sは非常に高い = {4、6}
- S = {{1、3}、{2、5、7}、{4、6}}
ソリューションInfluenzaの属性の値に応じたセットUのパーティションの形式は次のとおりです。
- S はい = { 2、6、7、8 }
- S no = {1、3、4、5}
- S = {{2、6、7、8}、{1、3、4、5}}
この表に示されているデータ、たとえばU 5とU 7は矛盾しており、U 6とU 8が繰り返されています。
| U 5 | いや | 高い | いや |
| U 6 | いや | 非常に高い | はい |
| U 7 | いや | 高い | はい |
| U 8 | いや | 非常に高い | はい |
実際には、近似セットを使用して、「有用な」不正確で矛盾したデータから「抽出」できます。
私たちは何に取り組みますか?
以下の投稿では、この理論を使用したデータ分析の実用的な実装(Python)を示します。
- 「IF ... THEN ...」などの決定ルールで構成される意思決定アルゴリズム
- 「IF ... THEN ...」タイプの決定ルールを生成するためのLEMアルゴリズム、LEM2 [Grzymała-Busse、1992]