この問題は、1つのプロジェクトのフレームワーク内での計算と、多孔質媒体の流体力学に関する将来の修士論文で形成されました。 ルーツの一部が著者の個人的な湾曲に隠れていることや、少数の処理に関する一般的なよく知られているヒントを無視していることを隠しませんが、それでも非常に興味深い観察と思考につながりました。
物理的本質を破棄する場合、問題は7つの偏微分方程式のシステムを解く必要があることです。 すぐに言って、特に困難はありません。明示的な有限差分スキームを作成し、OpenMPに並列化し、最終的な構文デバッグと速度の最適化の後、 「マシンが音を立て始めます。 」
コンピューティング構成:搭載されたCore 2 Duo 1.8 GHzを搭載したふりをしたHP 550、Ubuntu 11.04を実行。
コンパイラ:gfortran 4.5.2およびIntel Fortran Compiler 12.1.0。
初期状態では、計算領域内に液体状態の水はまったくないと想定されています。これは、相転移の過程で現れます。 そして、この欠席がパフォーマンスに大きな役割を果たしました。
そのため、この地域には水がありません。 初期状態で何を書きたいですか? 当然、0.0D + 00はすぐに書き込まれました(プログラムは実数の倍精度で書き込まれました)。 初期段階の計算は、マシンゼロのすぐ近くで行われます。 結果は何ですか? チャートを見てみましょう:
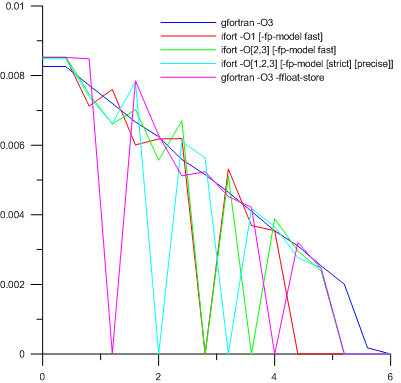
これは、モデルの物理的時間の1日以上後の計算ドメインの最も興味深い部分の座標に沿った間隙水飽和の分布を示しています。
チャートの凡例の署名に関する必要な余談:合計で18の異なるキーの組み合わせ(gfortranの場合は6、ifortの場合は12)がテストされましたが、それらの多くはまったく同じ結果をもたらしたため、組み合わせられました。 凡例の角かっこは、それらに囲まれたオプションを記述できることを意味します。 たとえば、「暗号化」-O [1,2,3] [-fp-model [strict] [precise]]は、考えられるすべてのレベルの最適化でコンパイラーが使用され、1つの浮動小数点モデルを含めることができることを意味します。 (含まれない可能性があります)。 3つのオプション(-fp-modelから2つとそれなしの1つ)に3つの最適化レベル(合計9つの組み合わせ)が乗算されます。 それらはすべて同等であることが判明しました。
そして今、結果。 IEEE 754標準(-ffloat-store key)への準拠を可能にすることなく、gfortranでのみ現実的かつ物理的に可能なものが得られました。 線の残りのカオスには、物理的な意味の低下が含まれていません。数学的にも、方程式ではこれが許可されていないためです。 差分スキームの最初の不安定性は、それを処理する方法が成功に至らなかったため正当化されました。
最初の瞬間に水の存在下では、スコアは安定したままであり、オプションとコンパイラーの違いは、6番目の有効数字の近くに隠れていることがわかりました。 そしてなぜなら 得られたグラフから判断すると、特性の次数は1.0e-2の領域にある必要があります。その後、初期条件に特定のゼロ以外の値(ただし非常に小さい値)が刻まれました。 この選択により、8バイトの実数に対して少なくとも1.0e-21であることが確立されました。 それから:
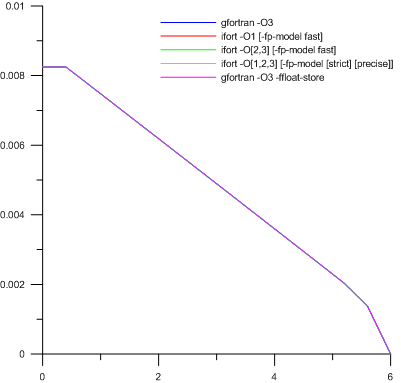
はい、ここで、伝説に書かれているように、実際には5つのグラフがあります。 ただ、6番目の有効数字の範囲内でまさにその差を得ることができます。
理由は? それは非常に明白です。 それらは、多数と少数の同時処理の複雑さにあります。 そして、現象がその範囲において非常に重要であるという事実は、一般的に予想されていました。 しかし、まず第一に、gfortran 4.5.2の相対的な成功を背景にした、Intelの非常に優れたツールの不安定性に関心があります。 最適化が有効で、アクセス可能なクラスターに他のオプションがインストールされていない(Slamd64を実行している)gfortran 4.1.2の古いバージョンでの計算中にも同様の問題が見つかったが、注意が払われなかったことは注目に値する。
奇妙なことに、IEEE 754への準拠はgfortranにとって重要な役割を果たしました。 それがなければ、スコアは非常に安定して正確です。 Intelの発案者にとっては、とにかく正しく動作しなかったため、これはそれほど重要ではありませんでした。
それで、彼が見た理由についての結論と考え。
- 観測された計算動作の原因の役割の最も可能性の高い候補は、丸め数値の微妙さのようです。 なぜなら 値の初期分布ではゼロに設定され、最初のステップでは計算はほぼ機械精度の境界で実行されます。 したがって、これは顕著な結果の蓄積につながり、最終的な結果に現れます。
- アルゴリズムの精度の低下は、明らかに、7つの偏微分方程式の次元システムが解かれ、それぞれの変数が他の変数と大きく異なる独自の特性値を持っているという事実によっても引き起こされます。 スケールファクターを正しく選択すると、無次元の方程式系で、少なくとも大きさの順に近いすべての変数の値を取得できますが、システムを無次元化しようとする最初の試行中に微分の前に小さな初期係数が生じたため、この手順を拒否しました。
- なぜ浮動小数点標準に準拠していないgfortranが許容可能な結果を生成できるのかという問題は、未解決のままです。 標準とは異なる独自の丸め規則が存在することを前提とするのは妥当です。これにより、安定したアカウントの維持と、コンパイラの開発中の修正と改良が保証されます。 「壊れやすいミスのバランス」またはアプローチの思慮深い修正? 悲しいかな、コンパイラをテストしてプロパティを調べるのではなく、主にコンパイラの使用を目的としたツールに関する私の知識レベルでは、これは不明です。 しかし、大学での数値的手法のトレーニングの最初の段階で与えられたプログラムの特定の場所で、精度が失われる可能性についての警告を考えて思い出すことができます。
コンパイラーは、ウィリアムカハンによるFORTRANバージョンの浮動小数点パラノイアを使用して、IEEE 754準拠についてテストされました。