アルゴリズムの一般的な考え方はこれです。
サイズN * N(N> = 4は2のべき乗)のフィールドの正方形があると仮定します。 次に、T = N / 4ステップの観点から、サイズ(N / 2)*(N / 2)の中央領域の状態を一意に決定できます。 元の正方形の状態とその進化の結果を辞書で覚えていれば、次にそのような正方形に出会ったときに、すぐにそれがどうなるかを判断できます。
N * N個の正方形について、N / 4ステップで進化を数えることができると仮定します。 正方形の2N * 2Nがあるとします。 N / 2ステップでの開発を計算するには、次のことができます。
正方形を辺N / 2の16個の正方形に分割します。 辺Nで9個の正方形を作り、それぞれについてN / 4ステップの進化の結果を見つけます。 サイドN / 2で9マスを取得します。 順番に、我々はすでにそれらの4つの正方形を辺Nで作り、それらのそれぞれについてN / 4ステップによる進化の結果を見つけます。 結果のサイドN / 2の4つの正方形は、サイドNの正方形に結合されます-それが答えとなります。
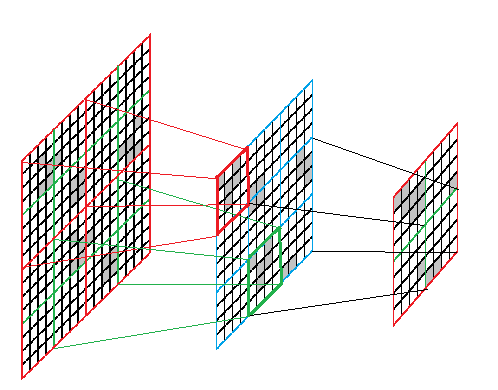
アルゴリズムを実装するには、次のことができる必要があります。
- 正方形を4つの正方形に分割します。
- 正方形の進化の結果を見つけます。
- 4つの正方形からそれらで構成される正方形を見つけます。
正方形の構築時に進化の結果を探す場合、5つのフィールドを持つ構造があれば十分です。
クラスSquare {
内部スクエアLB、RB、LT、RT、Res。
}
次に、4つの正方形を1つに結合するアルゴリズムは次のように記述できます。
Square Unite(Square a0、Square a1、Square a2、Square a3){
Square res = FindInDictionary(a0、a1、a2、a3);
if(res!= null)resを返します。
// T = N / 4のレイヤー
正方形b1 =結合(a0.RB、a1.LB、a0.RT、a1.LT).Res;
正方形b3 =結合(a0.LT、a0.RT、a2.LB、a2.RB).Res;
正方形b4 =結合(a0.RT、a1.LT、a2.RB、a3.LB).Res;
正方形b5 =結合(a1.LT、a1.RT、a3.LB、a3.RB).Res;
正方形b7 =結合(a2.RB、a3.LB、a2.RT、a3.LT).Res;
// T = N / 2のレイヤー
正方形c0 =結合(a0.Res、b1、b3、b4).Res;
正方形c1 =結合(b1、a1.Res、b4、b5).Res;
正方形c2 =結合(b3、b4、a2.Res、b7).Res;
正方形c3 =結合(b4、b5、b7、a3.Res).Res;
AddToDictionaryを返します(新しい正方形(){LB = a0、RB = a1、LT = a1、RT = a3、Res = Unite(c0、c1、c2、c3)});
}
実際には、それだけです。 ささいなこと:
再帰を停止します。 これを行うには、4×4の正方形すべてと1ステップずつの進化の結果を辞書に入力します(実際、この場所でのみ、プログラムはゲームのルールの知識を必要とします)。 2 * 2の正方形の場合、半ステップの進化は計算されず、特別な方法でマークされます。
進化ステップの数を2倍にします。 アルゴリズムに関しては、これは元のフィールドを含む正方形のサイズを2倍にすることと同じです。 正方形を中心に残し、それにゼロを追加したい場合、これを行うことができます:
スクエアエキスパンド(スクエアx){
正方形c0 =結合(ゼロ、ゼロ、ゼロ、x.LB);
正方形c1 =結合(ゼロ、ゼロ、x.RB、ゼロ);
正方形c2 =結合(ゼロ、x.LT、ゼロ、ゼロ);
正方形c3 =結合(x.RT、ゼロ、ゼロ、ゼロ);
Unite(c0、c1、c2、c3)を返します。
}
ここで、ゼロは特別な正方形であり、すべての部分とその結果は自分自身に等しくなります。
または、単にアクションx =結合(x、ゼロ、ゼロ、ゼロ)とx =結合(ゼロ、ゼロ、ゼロ、x)を交互に実行できます。 元の正方形は中央のどこかにあります。
辞書を実装します。 ここでは、美しい解決策は見つかりませんでした。キーでオブジェクトを検索する必要があります。これは、このオブジェクトの80%です(残りの20%だけでなく、オブジェクト自体も検索する必要があります)。 さまざまな種類のコレクションをいじって、手を振ってFortranで行動しました。5つの整数配列(LT、RT、LB、RB、Res)について説明し、正方形はこれらの配列の整数インデックスによって決まります。 0〜15のインデックスは、2 * 2の正方形用に予約されています。 長さの2倍の6番目の配列は、ハッシュに使用されます。
また、フィールドを設定して結果を読み取る必要がありますが、これは技術の問題です。 読み取りに注意する必要がありますが、Expandを63回以上実行すると、フィールドの辺の長さが64ビットに収まりません。
そのような構成でアルゴリズムをテストしました:
「ごみディスペンサー。」

c / 2の速度で移動し、背後に多くの破片を残し、240ステップごとに2、3個のグライダーを放出します。 0.73秒で1兆世代(より正確には2 ^ 40)が計算されました。 約120,000平方(時間の倍増ごとに1,500)が辞書に落ち、フィールド上の生きた細胞の数は6,000億です。
結果のフィールドのフラグメントは次のようになります。
(2001x2001、82 KB)
グライダー銃の戦い
2つのグライダーガンは互いに800セルの距離にあり、放出されたストリームは衝突します。
(T = 2048、804x504、11 KB)
衝突後すぐに、グライダーが破片の山から飛び出し、最初に1つの銃を破壊します。
(T = 4096、1098x1024、30 Kb)
そして、2番目(その後、開発はすぐに終了します):
(T = 8192、3146x3252、190 Kb)
カウント時間は0.84秒で、辞書の要素数は約270,000です。
「ランダム充填」
フィールド1024 * 1024には、1/3の密度のセルがランダムに入力されます。 アルゴリズムの場合、これが最も難しいケースです。構成がゆっくりと安定し、正方形がすぐに繰り返されなくなります。
構成の1つを開発する例を次に示します。
(T = 0、1024x1024、300 Kb)
(T = 1024、1724x1509、147 Kb)
(T = 2048、2492x2021、177 Kb)
(T = 4096、4028x3045、300 Kb)
(T = 8192、7100x5093、711 Kb)
カウント時間は14秒、ディクショナリの要素数は約1500万、フィールドには約35,000ポイントが残っています。
このアルゴリズムの異常な点は何ですか? 次のことに注意してください。
- ほとんど手間をかけずに、空の領域をアクティブな領域から分離し、アクティブな領域を追跡し、それらの相互作用を解決できるプログラムを手に入れました。 多くの動的な2次元配列を使用してこのような分析を直接記述した場合、プログラムははるかに複雑になります。
- このアルゴリズムは、Tステップでフィールドの状態を計算するだけでなく、開発全体を記憶します。 彼の仕事の結果から、任意の間隔T_k = 2 ^ kで状態を簡単に抽出できます(2のべき乗ではない時間の後にフィールドの状態を取得する方法は別の質問です)。 同時に、全体の進化は十分に詰め込まれていることがわかりました-再び、特別な努力なしで:2 ^ 40世代の「ごみ収集車」が3 MBに収まりました。
- 辞書は初期構成に従って構築されるという事実にもかかわらず、その内容はこの構成に依存しません。 計算が完了したら、新しい辞書に同じ辞書を使用できます。運が良ければ、多くの時間を節約できます(試しませんでした)。
- 正式には、平面上の構成は4ツリーの形式で表示されます。 しかし、隣接するブランチの極端なポイント間の相互作用を分析するために、これらのポイントに明示的には行かず、1〜2ステップだけ下がってから、問題の解決に適したツリーを探して構築します。 ただし、ここで異常なことは何もありません。新しいノードの構築のために時間を無駄にしないで、むしろ逆に。
- アルゴリズムでは、「原子」セルの実際のサイズもその状態の数もどこでも使用されません。 再帰が到達できる最低レベルは、16個の状態を持つセルであり、2×2個の正方形として認識されます。 このレベルの時空(アルゴリズムの場合)は、顔を中心とした格子(黒のセルのみが取得された3次元のチェス盤)のように見えます。 私たちがコンウェイのルールに基づいて発明した16番。 アルゴリズムでは、何でもかまいませんが、メインコードはそれに依存しません