相互作用する多数の粒子のモデリング

オブジェクト間の衝突を処理する必要がある状況を考えます。 この場合、あなたは何をしますか？ おそらく最も簡単な解決策は、すべてのオブジェクトを他のすべてのオブジェクトでチェックすることです。 そして、これは正しい決定であり、多くのオブジェクトが存在しない限り、すべてがうまくいきます。 それらが数千個あるとすぐに、すべてが何らかの形でゆっくりと働き始めたことがわかります。 そして、粒子が数万または数百の場合はどうなりますか？ その後、すべてがフリーズします。 ここでは、このような問題を解決するためにどのようなトリックと最適化を行うかがすでに興味深いです。



簡単にするために、2Dの場合を考えます。粒子は丸く、粒子の半径はすべて同じです。

内容

1.アルゴリズムの概要

1.1。 完全検索

1.2。 スイープとプルーン

1.3。 通常のネットワーク

2.いくつかの最適化

2.1。 スイープとプルーン

2.2。 通常のネットワーク

3.実行速度の比較

4.アプリケーション（プログラムとソースコード）

5.結論

1.アルゴリズムの概要

1.1。 完全検索

これは、最も簡単な方法であると同時に、可能なすべての方法の中で最も遅い方法です。 考えられるすべてのパーティクルペア間でチェックが行われます。

void Update() { for (int i = 0; i < NUM_P; ++i) { for (int j = i + 1; j < NUM_P; ++j) { Collision(&_particles[i], &_particles[j]); } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

難易度： O（n ^ 2）



長所：

*理解と実装が非常に簡単

*異なる粒子サイズの影響を受けない

短所：

*最も遅い

1.2。 スイープとプルーン

このアルゴリズムの本質は、最初にすべての粒子をOX軸に沿って左境界線で並べ替え、次に各粒子を左境界線が現在の粒子の右境界線よりも小さい粒子のみでチェックすることです。



写真でアルゴリズムの動作を説明しようとします。

初期状態：



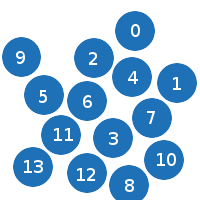
ご覧のとおり、パーティクルは順序付けられていません。

パーティクルの左境界線（X位置からパーティクル半径を引いたもの）でソートした後、次の図が表示されます。



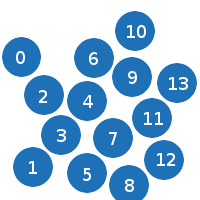
これで、バスティングを開始できます。 最初のパーティクルの右の境界が2番目のパーティクルの左の境界より大きくなるまで、各パーティクルを互いに確認します。



例を考えてみましょう。

0パーティクルは1および2との衝突をチェックします：



1と2および3。

2は3のみ。

3は、4、5、および6との衝突をチェックします。



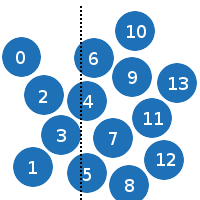
その点は明らかだと思います。



このアルゴリズムの私の実装：

 void Update() { qsort(_sap_particles, NUM_P, sizeof(Particle *), CompareParticles); for (int i = 0; i < NUM_P; ++i) { for (int j = i + 1; j < NUM_P && _sap_particles[i]->pos.x + RADIUS_P > _sap_particles[j]->pos.x - RADIUS_P; ++j) { Collision(_sap_particles[i], _sap_particles[j]); } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアルゴリズムは、各瞬間の粒子の動きが小さい場合に最も効果的であることに注意してください。 ソートは主な負荷を引き継ぎ、パーティクルがすでに部分的にソートされている場合は高速になります。



このアルゴリズムは、より複雑なオブジェクトにも使用できます。その場合は、AABB（Axis-Aligned Bounding Box、最小境界ボックス）を使用する必要があります。



難易度： O（n ^ 2）-最悪の場合、O（n * log（n））-平均的な場合



長所：

*実装が簡単

*異なる粒子サイズの影響を受けない

*良好なパフォーマンス

短所：

*アルゴリズムを理解するには少し時間がかかります

1.3。 通常のネットワーク

おそらく名前から推測したように、アルゴリズムの本質は、空間全体が粒子の直径に等しいサイズの小さな正方形の均一なネットワークに分割されることです。 このネットワークの各正方形（セル）は配列です。

これは、たとえば次のようになります。

  const int _GRID_WIDTH = (int)(WIDTH / (RADIUS_P * 2.0f)); const int _GRID_HEIGHT = (int)(HEIGHT / (RADIUS_P * 2.0f)); std::vector<Particle *> _grid[_GRID_WIDTH][_GRID_HEIGHT];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

メインループの各反復で、このネットワークはクリアされ、再充填されます。 充填アルゴリズムは非常に簡単です。粒子セルインデックスは、両方の座標を粒子直径で除算し、小数部分を破棄することで計算されます。 例：

  int x = (int)(_particles[i].pos.x / (RADIUS_P * 2.0f)); int y = (int)(_particles[i].pos.y / (RADIUS_P * 2.0f));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、パーティクルごとに、インデックスを計算し、このインデックスを使用してセルに追加する必要があります（要素を配列に追加します）。

これで、各セルを通過し、その周囲の隣接する8つのセルのすべての粒子ですべての粒子をチェックするだけで、自身でチェックすることを忘れることはありません。



これは次のように実行できます。

  void Update() { for (int i = 0; i < _GRID_WIDTH; ++i) { for (int j = 0; j < _GRID_HEIGHT; ++j) { _grid[i][j].clear(); } } for (int i = 0; i < MAX_P; ++i) { int x = (int)(_particles[i].pos.x / (RADIUS_P * 2.0f)); int y = (int)(_particles[i].pos.y / (RADIUS_P * 2.0f)); _grid[x][y].push_back(&_particles[i]); } //        }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

難易度： O（n）



長所：

*すべての最速

*実装が簡単

短所：

*追加のメモリが必要

*異なる粒子サイズに敏感（変更が必要）

2.いくつかの最適化

2.1。 スイープとプルーン

このアルゴリズムは、粒子を並べ替える軸を選択することでわずかに改善できます。 最適な軸は、それに沿って最大数の粒子が位置する軸です。

最適なOY軸：

最適なOX軸：

2.2。 通常のネットワーク

最適化番号1：

ネットワークのより効率的な表現を使用します。

  const int _MAX_CELL_SIZE = 4; const int _GRID_WIDTH = (int)(WIDTH / (RADIUS_P * 2.0f)); const int _GRID_HEIGHT = (int)(HEIGHT / (RADIUS_P * 2.0f)); int _cell_size[_GRID_WIDTH * _GRID_HEIGHT]; Particle *_grid[_GRID_WIDTH * _GRID_HEIGHT * _MAX_CELL_SIZE];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

1次元配列は2次元配列よりも高速であり、一定の長さの静的配列は動的std ::ベクトルよりも高速であることは言うまでもありません。これらすべてを組み合わせたという事実は言うまでもありません。 また、別のアレイを開始する必要がありました。これは、各セルにいくつのパーティクルがあるかについて説明します。

そして、はい、セル内の粒子の数に制限を導入しましたが、これは完全に良いわけではありません。 強い圧縮では、はるかに多くの粒子をセルに書き込む必要があり、 これは不可能であり、一部の衝突は処理されません。 ただし、衝突を適切に解決すれば、この問題を回避できます。



最適化№2

メインループの各反復でグリッド配列を完全にクリアする代わりに、発生した変更のみを行います。

ネットワーク内の各セルのすべてのパーティクルを調べ、新しいパーティクルインデックスを計算し、現在のインデックスと等しくない場合は、現在のセルからパーティクルを削除して、新しいセルの空きスペースに追加します。

同じセルからの最後の粒子をその場所に記録することにより、除去が行われます。

これを実装するコードは次のとおりです。

  for (int i = 0; i < _GRID_WIDTH * _GRID_HEIGHT; ++i) { for (int j = 0; j < _cell_size[i]; ++j) { int x = (int)(_grid[i * _MAX_CELL_SIZE + j]->pos.x / (RADIUS_P * 2.0)); int y = (int)(_grid[i * _MAX_CELL_SIZE + j]->pos.y / (RADIUS_P * 2.0)); if (x < 0) { x = 0; } if (y < 0) { y = 0; } if (x >= _GRID_WIDTH) { x = _GRID_WIDTH - 1; } if (y >= _GRID_HEIGHT) { y = _GRID_HEIGHT - 1; } //            if (x * _GRID_HEIGHT + y != i && _cell_size[x * _GRID_HEIGHT + y] < _MAX_CELL_SIZE) { _grid[(x * _GRID_HEIGHT + y) * _MAX_CELL_SIZE + _cell_size[x * _GRID_HEIGHT + y]++] = _grid[i * _MAX_CELL_SIZE + j]; //           _grid[i * _MAX_CELL_SIZE + j] = _grid[i * _MAX_CELL_SIZE + --_cell_size[i]]; } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最適化番号3

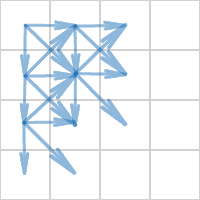
隣接する8つのセルで検証を使用します。 これは冗長です。4つの隣接セルのみをチェックすれば十分です。

たとえば、次のように：



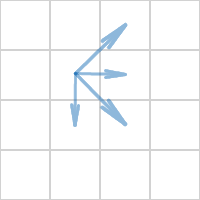
残りのセルでは、チェックは早いか遅いかのいずれかに合格します。





最適化№4

メモリ内のデータの局所性を高めることで、アルゴリズムをわずかに高速化できます。 これにより、プロセッサキャッシュからデータをより頻繁に読み取ることができ、RAMへのアクセスが少なくなります。 ただし、メインループの各反復でこれを行わないでください。 これによりすべてのパフォーマンスが低下しますが、この操作は、たとえば1秒に1回、シーンがわずかに変化する場合は数秒に1回実行できます。

ネットワーク上の位置に応じて、メインアレイ内の粒子の順序を変更することにより、局所性を高めることができます。

つまり 最初の4個の粒子は0個のセルから、次の4個の粒子は1個からという具合になります。

3.実行速度の比較

粒子数	ブルートフォース（ミリ秒）	スイープとプルーン（ミリ秒）	通常のネットワーク（ミリ秒）
1000	4	1	1
2000年	14	1	1
5000	89	4	2
10,000	355	10	4
20000	1438	28	7
30000	3200	55	11
100,000	12737	140	23

表からわかるように、アルゴリズムの実行時間はその複雑さに対応し、通常のネットワークはほぼ直線的に成長します:)。

4.アプリケーション（プログラムとソースコード）

http://rghost.ru/35826275



アーカイブには、CodeBlocksで書かれたプロジェクトとLinuxのバイナリが含まれていますが、 ウィンドウを作成してグラフィックを表示するには、ClanLibライブラリを使用しました。その後、プロジェクトはWindowsで問題なくコンパイルされるはずです。



プログラムの管理：

番号1-ブルートフォース

番号2-スイープとプルーン

番号3-規制ネットワーク

マウスの左ボタン-「プッシュ」を移動します。

5.結論

この記事では、衝突の処理に使用される最も一般的なアルゴリズムの概要を簡単に説明します。 ただし、これはこれらのアルゴリズムの範囲を制限するものではなく、他の相互作用に使用されることを妨げるものは何もありません。 彼らが自分自身に課す主なタスクは、データのより便利なプレゼンテーションです。そのため、彼らは事前に興味のないペアをすばやく除外することができます。