ハブレに関する議論からわかるように、数十人のハブロフスク市民がスタンフォード大学のml-class.orgのコースに参加しました。これは魅力的な教授Andrew Ngによって行われました。 このコースを聞くのも楽しかったです。 残念ながら、計画で述べられた非常に興味深いトピックは講義から外れました。教師との指導と教師なしの指導の組み合わせです。 判明したように、Ng教授はこのトピックに関する優れたコースを公開しました-教師なしの特徴学習と深層学習（自発的な特徴抽出と深層学習）。 このコースの簡単な要約を、厳密な説明と豊富な数式なしで提供します。 オリジナルにはすべてがあります。
イタリック体は、元のテキストの一部ではない挿入部分に入力されますが、抵抗することはできず、自分のコメントと考慮事項を含めました。 原作者のイラストを恥知らずに使用したことについて著者に謝罪します。 また、英語からのいくつかの用語の直接翻訳についても謝罪します（たとえば、空間オートエンコーダ->スパースオートエンコーダ）。 私たちスタンフォードはロシアの専門用語をよく知りません:)
スパース自動エンコーダー
最も一般的に使用される直接分布のニューラルネットワークは、教師とのトレーニングを目的としており、たとえば分類に使用されます。 このようなニューラルネットワークのトポロジの例を図に示します。
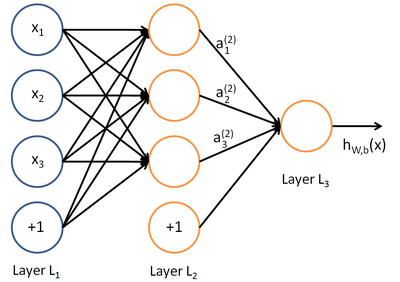
このようなニューラルネットワークのトレーニングは、通常、トレーニングサンプルのネットワーク応答の二乗平均平方根誤差を最小化するような方法で、誤差の逆伝播の方法によって実行されます。 したがって、トレーニングセットには、特徴ベクトル（入力データ）と参照ベクトル（ラベル付きデータ）のペア{（x、y）}が含まれます。
ここで、ラベル付きデータがなく、特徴ベクトル{x}のセットだけがあることを想像してください。 自動エンコーダーは、教師なしの学習アルゴリズムであり、ニューラルネットワークと逆伝播法を使用して、入力特徴ベクトルが入力ベクトルに等しいネットワーク応答を引き出すようにします。 y = x 自動エンコーダーの例：
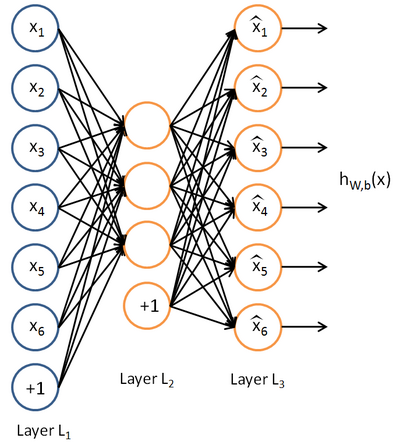
Auto Encoderは関数h（x）= xを構築しようとしています。 つまり、ニューラルネットワークの応答が入力フィーチャの値にほぼ等しくなるように、そのような関数の近似値を見つけようとします。 この問題の解決を簡単にするために、ネットワークトポロジに特別な条件が課されます。
•隠れ層のニューロンの数は、入力データの次元（図のように）より少ない必要があります。または
•隠れ層のニューロンの活性化はまばらでなければなりません。
最初の制限により、入力信号をネットワーク出力に送信するときにデータ圧縮が可能になります。 たとえば、入力ベクトルが10x10ピクセル（合計100属性）の画像輝度レベルのセットであり、非表示層のニューロンの数が50である場合、ネットワークは画像圧縮の学習を強制されます。 実際、要件h（x）= xは、隠れ層の50個のニューロンの活性化レベルに基づいて、出力層が元の画像の100ピクセルを復元することを意味します。 データに隠された関係、属性の相関、および一般的に何らかの構造がある場合、このような圧縮が可能です。 この形式では、自動エンコーダーの操作は、入力データの次元が削減されるという意味で、主成分分析（PCA）の方法と非常に似ています。
2番目の制限-隠れ層ニューロンの疎活性化の要件-は、隠れ層ニューロンの数が入力データの次元を超える場合でも、重要な結果を得ることができます。 非公式にスパース性を説明する場合、伝達関数の値が1に近いときにニューロンがアクティブであると見なします。 スパースアクティベーションとは、隠れ層の非アクティブニューロンの数がアクティブニューロンの数を大幅に超える場合です。
pの値を隠れ層ニューロンの活性化の平均値（トレーニングサンプル全体）として計算する場合、逆伝播法によるニューラルネットワークの勾配学習で使用される目的関数に追加のペナルティ項を導入できます。 式は元の講義にあり、ペナルティ係数の意味は回帰係数の計算における正則化手法に似ています。pが所定のスパースネスパラメータと異なる場合、誤差関数は大幅に増加します。 たとえば、トレーニングサンプルの平均アクティベーション値を0.05にする必要がある場合があります。
隠れ層ニューロンのわずかな活性化の要件は、驚くべき生物学的アナロジーを持っています。 脳の構造の元の理論の著者であるジェフ・ホーキンスは、ニューロン間の抑制的接続の基本的な重要性に注目しています（ロシア語のテキストHierarchical Temporal Memory（HTM）とその皮質学習アルゴリズムを参照）。 同じ層にあるニューロン間の脳では、多数の「水平方向の接続」があります。 大脳皮質のニューロンは非常に密接に相互接続されていますが、多数の抑制性（抑制性）ニューロンが一度にすべてのニューロンのごく一部のみがアクティブになることを保証します。 つまり、利用可能なすべてのニューロンのうち、少数のアクティブなニューロンのみによって常に情報が脳に提示されることがわかります。 これにより、明らかに、脳は一般化を行うことができ、たとえば、車のようにあらゆる角度から車のイメージを知覚できます。
隠れ層関数の可視化
ラベルなしのデータセットで自動エンコーダーをトレーニングしたら、このアルゴリズムで近似された関数を視覚化することができます。 上記の10x10ピクセル画像でエンコーダーをトレーニングする例の視覚化は非常に明確です。 「入力xのどの組み合わせが、隠れニューロン番号iの最大の活性化を引き起こすか」ということを自問します。つまり、各隠れニューロンは、入力データのどのような特徴のセットを探しますか。
この質問に対する自明でない答えは講義に含まれており、100個のニューロンの隠れ層でネットワーク機能を視覚化するときに出てきたイラストに限定しています。
各正方形の断片は、隠れニューロンの1つを最大限に活性化する入力画像xを表します。 対応するニューラルネットワークは自然画像の例（たとえば、自然の写真の断片）を使用して訓練されたため、隠れ層のニューロンは、異なる角度から輪郭を検出する機能を独自に研究しました！
私の意見では、これは非常に印象的な結果です。 ニューラルネットワークは、独立して、多数の多様な画像を観察することにより、人間や動物の脳の生物学的構造に類似した構造を構築しました。 J.ニコルズなどの著書「ニューロンから脳へ」の次の図からわかるように、これは脳の下部の視覚部分の配置方法です。
この図は、視覚刺激に対する猫の縞模様の皮質の複雑な細胞の反応を示しています。 セルは、最適な方法で（ほとんどの出力パルス）垂直方向の境界に応答します（最初のフラグメントを参照）。 水平方向の境界線に対する反応は実質的にありません（3番目のフラグメントを参照）。 縞模様の皮質の複雑な細胞は、人工ニューラルネットワークの隠れ層にある訓練されたニューロンにほぼ対応しています。
隠された層のニューロンのセット全体は、さまざまな角度で輪郭（明るさの違いの境界）を検出することを学びました-ちょうど生物学的な脳のように。 「ニューロンから脳へ」という本の次の図は、ニューロンが猫の脳の皮質に深く入り込む際のニューロンの受容野の方向軸を模式的に示しています。 同様の実験により、ネコとサルで同様の特性を持つ細胞が、皮質の表面に対して特定の角度をなす列に配置されることが確認されました。 列内の個々のニューロンは、列内の各ニューロンに固有の特定の角度で回転した、白い背景に黒のストライプが付いた動物の視野の対応する部分の視覚刺激により活性化されます。
自己学習
信頼性の高い機械学習システムを取得する最も効果的な方法は、学習アルゴリズムにできるだけ多くのデータを提供することです。 大規模な問題を解決した経験によれば、トレーニングサンプルの量が100万〜1000万サンプルを超えると、定性的な移行が発生します。 教師と一緒にトレーニングするためにラベル付きデータをさらに取得しようとすることもできますが、これは常に可能ではありません（そして費用対効果が高い）。 したがって、ニューラルネットワークの自己学習にマークされていないデータを使用することは有望と思われます。
マークのないデータには、ラベルのあるデータよりもトレーニングに関する情報が少なくなります。 ただし、教師なしで学習できるデータの量ははるかに多くなります。 たとえば、画像認識タスクでは、インターネット上で利用できるデジタル写真の数に制限はなく、無視できる割合のデジタル写真のみがマークされます。
自己学習アルゴリズムでは、ニューラルネットワークに大量のマークされていないデータを提供し、そこからネットワークが有用な特徴を抽出することを学習します。 さらに、これらの機能を使用して、比較的小さいラベル付きトレーニングサンプルを使用して特定の分類器をトレーニングできます。
自己学習の最初の段階を、6つの入力と隠れ層の3つのニューロンを備えたニューラルネットワークの形で表現しましょう。 これらのニューロンの出力は、スパースオートエンコーダアルゴリズムによってラベル付けされていないデータから抽出される一般化された機能になります。
これで、ニューラルネットワークの出力層をトレーニングしたり、ロジスティック回帰、サポートベクターマシン、またはソフトマックスアルゴリズムを使用して、選択した機能に基づいて分類をトレーニングしたりできます。 これらの従来のアルゴリズムでは、マークされたトレーニングサンプルxmが入力として使用されます。 自己学習ネットワークのトポロジーには2つのオプションがあります。
•従来の分類器の入力（ニューラルネットワークの出力層など）では、符号aのみが与えられます。
•従来の分類器の入力（たとえば、ニューラルネットワークの出力層）では、符号aと入力符号xmが与えられます。
さらに、Ngの講義では、多層ネットワークとそのトレーニングでの自動エンコーダーの使用について説明します。