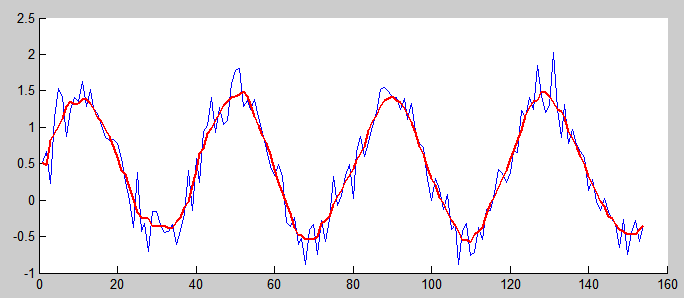
基本は、MATLABの滑らかな関数です。
この関数は、信号のフィルタリングに使用できます。 データの配列と平均化ウィンドウは、入力パラメーターとして定義されます。
誰が気にします、私はカットをお願いします
そのため、このアルゴリズムにはいくつかの実装があります。 最も簡単なものを考えてください:
平均化ウィンドウのサイズが5である場合、平均化の各ステップで現在の値が取得され、前の4つがそれに加算され、結果が5で除算されます。ここでの明らかな問題は、アルゴリズムの初期化にあります。
MATLABでは、移動平均フィルタリングアルゴリズムはsmooth関数で実装されています
smooth(input、window)を使用した例、
inputは入力データの配列です
window-平均化ウィンドウ。
ウィンドウパラメーターを変更することにより、データの平滑化の程度を増減できます。
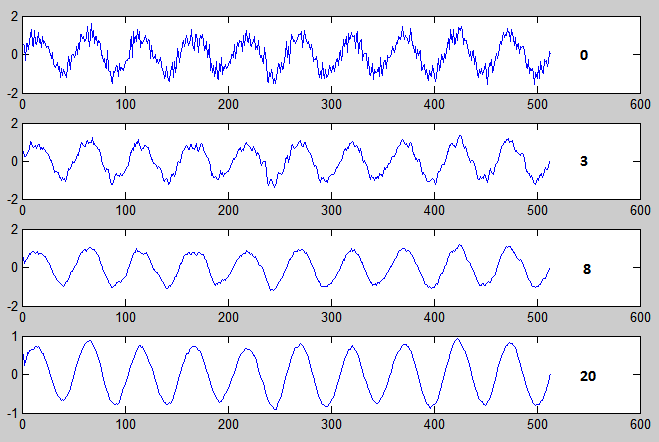
この例を実装するソースを以下に示します。
clear all; %% t=1;% Fd=512;% () A1=1;% F1=10;% () SNR=0.3;% / T=0:1/Fd:t;% Noise=A1*SNR*randn(1,length(T));% Signal=A1*sind((F1*360).*T);% SN=Signal+Noise; figure(1); subplot(4,1,1); plot(SN); subplot(4,1,2); plot(smooth(SN,3)); subplot(4,1,3); plot(smooth(SN,8)); subplot(4,1,4); plot(smooth(SN,20));
信号処理の遅延を補正するために、MATLABは動的にサイズ変更可能なウィンドウを使用します;メソッドの本質を次の例で示します。
最初にこのアルゴリズムの独自の実装をMATLABで作成してから、C ++に転送しました
MATLABエディション:
%my_smooth % , , 1 ; window = 5; if(mod(window,2)==0) window=window+1; end hw=(window-1)/2; % n=length(Signal); result=zeros(n,1); result(1)=SN(1); % SN for i=2:n % init_sum = 0; if(i<=hw) % , , % k1=1; % k2=2*i-1; % z=k2; % elseif (i+hw>n) % + n - % k1=i-n+i; % k2=n; % - z=k2-k1; % else % , k1=i-hw; k2=i+hw; z=window; end for j=k1:k2 % init_sum=init_sum+SN(j); % end result(i)=init_sum/(z); % end
このプログラムの結果は、奇数のウィンドウサイズで滑らかなmatlabと完全に一致し、偶数の値とはわずかに異なります(ウィンドウでも、matlabはわずかに異なると見なされます)。
ソースmファイルはここで取得できます
C ++エディション
void smooth(double *input, double *output, int n, int window) { int i,j,z,k1,k2,hw; double tmp; if(fmod(window,2)==0) window++; hw=(window-1)/2; output[0]=input[0]; for (i=1;i<n;i++){ tmp=0; if(i<hw){ k1=0; k2=2*i; z=k2+1; } else if((i+hw)>(n-1)){ k1=i-n+i+1; k2=n-1; z=k2-k1+1; } else{ k1=i-hw; k2=i+hw; z=window; } for (j=k1;j<=k2;j++){ tmp=tmp+input[j]; } output[i]=tmp/z; }
ご清聴ありがとうございました。建設的な批判は大歓迎です
PS:
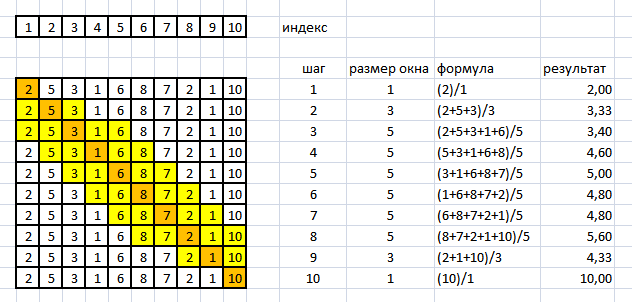
アルゴリズムは、合計の計算を変更することで速度を最適化できます。

4番目のステップで要素の合計を計算するには、3番目のステップで合計から配列の最初の要素(2、赤でマーク)を減算し、6番目の要素(8、黄色のセル)を追加する必要があることがわかります。
次のステップでは、手順が繰り返されます。
このアプローチは、平均化ウィンドウが大きい場合に効果的です。