幾何学的変換
はじめに、数学的な部分に触れてみましょう。 ベクトル行列形式で幾何学的変換を数学的に表すと便利です。 したがって、たとえば、与えられた画像点を特徴付ける半径ベクトルrがある場合、表示点の半径ベクトルr 'を取得するには、幾何変換行列Aにrを掛ける必要があります: r' = A・r 最も単純な場合、 Aは2次元の2x2行列です。 ただし、複雑な変換の場合は、3x3の次元に拡張する必要があります。たとえば、画像の変位を記述するためです。
一般的な場合、ベクトルrおよびr 'は、3つの要素の列ベクトルです。ポイントの座標と単位自体です。 3x3変換行列自体には6つの重要な要素(上の2行)しかなく、3行目には2つのゼロと1つの単位が含まれます。
この場合、マトリックス形式の角度θによる原点に対する回転の変換は、次のように記述されます。
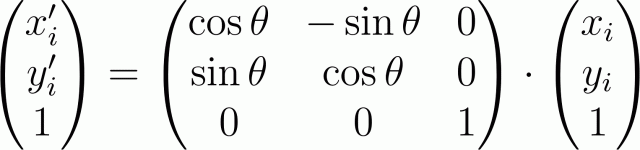
幾何学的変換行列の重要なメンバーには次の意味があります:左上隅の2x2サブマトリックスは、ポイントの座標に依存する変換(回転、スケーリングなど)を反映し、右端の列の上の2つのメンバーは、座標(オフセット)に依存しない変換を表します。
したがって、たとえば、ベクトルtによるこのシフトが続く角度θでの原点の周りの回転行列は、次のようになります。
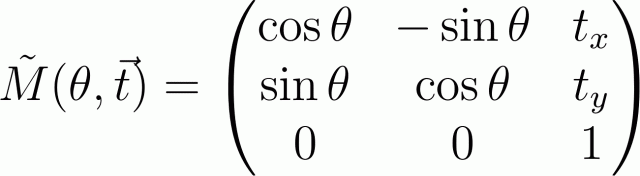
より複雑な変換を記述するマトリックスを取得するには、このモーションを基本的なモーション(回転、変位、スケーリング)に分解し、対応するマトリックスを乗算する必要があります。 openGLで作業したことがある人は、これを行うのに問題はありません。 変換がA、B、Cの順序で実行される場合、「後方」に乗算する必要があることに注意する必要があります。結果の行列M = C・B・A (変換Aは最初にA・rを乗算して実行されるため変換Bなどが行われます。
任意の点の周りの回転は、3つの基本的な変換に分解されます:原点が回転点にあるように画像をシフトします(つまり、回転の中心が点(x、y)にある場合、ベクトル(-x、-y)でシフトする必要があります) ; 角度θによる回転とベクトル(x、y)による逆シフト。 この乗算の結果、変換行列は次の形式になります
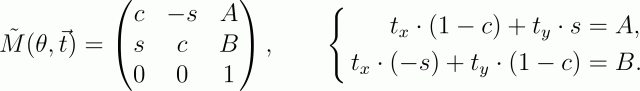
(表記を簡単にするために、sinθをsに、cosθをcに置き換えました)。
回転行列の重要な項を行列Rとして表すと、最後の連立方程式は行列形式(IR)・t = ABで表すことができます。ここで、 ABは最終変換行列の項AとBからの列ベクトルです。
ここから、画像の中心を特徴付けるベクトルtを見つけることができます: t =(IR)\ AB 、ここでバックスラッシュは「左」除算の操作を示します(MatlabとOctaveで採用されたエントリ):代数では、これは表記t =(IR) -1に似ていますAB ( Iは単位行列です)。
回転に小さな変位が伴う場合、ベクトルABには加算項drが含まれます。これにより、計算に大きな誤差が生じます(小さな角度で回転するとベクトルABの回転が小さくなるため)。 この変位を数学的に決定することは不可能であり、手に持っているショットは数個だけです。 ただし、かなりの数の画像がある場合は、回転中心の中央値を計算できます。これを知っていれば、小さな変位drを簡単に決定できます。
Octaveでの実装
それで、星のフィールドの画像のセットを持ってみましょう(ちなみに、これは確実に区別された参照領域を持つ任意の画像かもしれません)そして、このフィールドの回転の中心を計算する必要があります。
まず、星を選択する必要があります(一般的な場合、参照点)。 特定の場合、これは特定のしきい値での単純な2値化によって解決されます(しきい値は、ユーザーが指定した値の最大値と、画像の中央値と標準偏差の1/4の合計として選択されます)。 さらに、結果のバイナリイメージでは、8連結性のゾーンが検出され、検出順に番号が付けられます。 その結果、オブジェクトの中心を計算できるマスクのセットを取得します(最も単純な場合、基本的な重心として)。
次に、すべての画像に存在するオブジェクトを強調表示する必要があります。 この問題を「正面から」解決しました。各画像に対してベクトルのセットが構築されます-各オブジェクトに対する極座標系で検出されたオブジェクトの座標(つまり、Nポイントのセットに対してN・(N-1)ベクトルを取得します)。 識別のために、最初の画像とi番目の画像のベクトルのすべてのセットがソートされます。 各セットには推定値が与えられます。これは、ユーザー定義の誤差dr、dφまでの点の半径ベクトルの一致数です。 次に、最も高い評価を持つセットのペアが選択され、i番目の画像のオブジェクトには、最初の画像のオブジェクトの順序に従って番号が付けられます。 最初の画像のオブジェクトを検出する各手順の後、最初の画像の検出されたオブジェクトに対応するカウンターの値はi番目の値で増加します。 並行して、検出されたオブジェクトの座標が蓄積されます。
この「正面」のソリューションは、検出されたオブジェクトの数が多く、画像の数が多い場合、計算を大幅に遅くし、大量のメモリを消費するため、この方法を簡素化できます。 たとえば、最初に最初の画像と最後の画像を比較して、一連のポイントを決定できます(これにより、メモリ消費と反復回数が削減されます)。 検索自体は、最初の画像の2つまたは3つのオブジェクトに対してのみ実行できます(特定のオブジェクトがi番目の画像で検出されない可能性があるため、1セットのみの比較は使用できません)。
オブジェクトの検出後、カウンターの配列を取得します。 オブジェクトがすべての画像に存在する場合、対応するカウンターの値はM-1に等しくなければなりません(Mは画像の数です)。 カウンターがM-1に等しくないすべてのデータが削除されます。 次に、すべての画像のオブジェクトの座標をペアで比較し、上記の式を使用して各ペアの回転の中心を計算するだけです(変換行列は最小二乗法で計算されます)。 中心座標の配列を蓄積すると、すべての座標の中央値として実際の回転中心がわかります。
私の方法に加えて、 この記事で別の方法を見つけました(McKein et al。)。 この方法は、最小二乗法で変換行列を見つける必要がないという点で便利です。 これは、任意の点の周りの回転をより簡単に表すことができるという事実に基づいています。つまり、原点および後続の変位に対する直接の回転としてです。 著者は、変換行列を計算する代わりに、システム全体の回転角を決定することを提案しました(これは、オブジェクトの重心に対する極座標系のオブジェクトの座標表現を使用して簡単に実行できます)。 回転角から、回転行列Rが計算されます。 この行列に最初の画像のオブジェクトの半径ベクトルを掛けると、変位ベクトルv (i番目の画像のオブジェクトの半径ベクトルと取得した半径ベクトルの差の中央値)を求めます。 回転の中心は、同じ式t =(IR) -1 vを使用して計算されます。
大量の統計資料では、両方の方法で同じ結果が得られました。 どちらの方法を選択するかは、実装によって決まります。たとえば、Octaveでは、私のメソッドはより高速に計算され、両方のメソッドの実装は単純です。 Cでアルゴリズムを実装すると、McKeinチームメイトの方法が簡単になります。
見つかった中心の座標の散布図は次のとおりです。
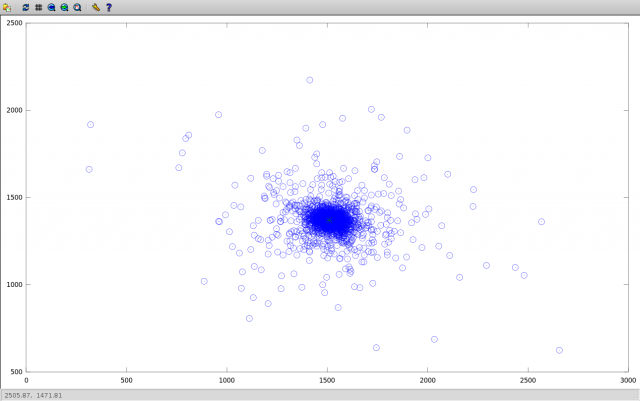
外れ値は、隣接する画像(回転角が小さい)を比較すると、変位の計算で非常に高い誤差が得られるという事実によって説明されます。これは、オブジェクトの座標の計算での誤差に匹敵します。 中央値に対して検出された座標の絶対偏差は、上記を示しています。

(近い画像に典型的な放射は、回転角度の増加とともに急激に減少します)。 中央値平均により、これらの外れ値を削除できます。
はい、スターフィールドの画像の例を挙げるのを忘れていました。 ここにあります:
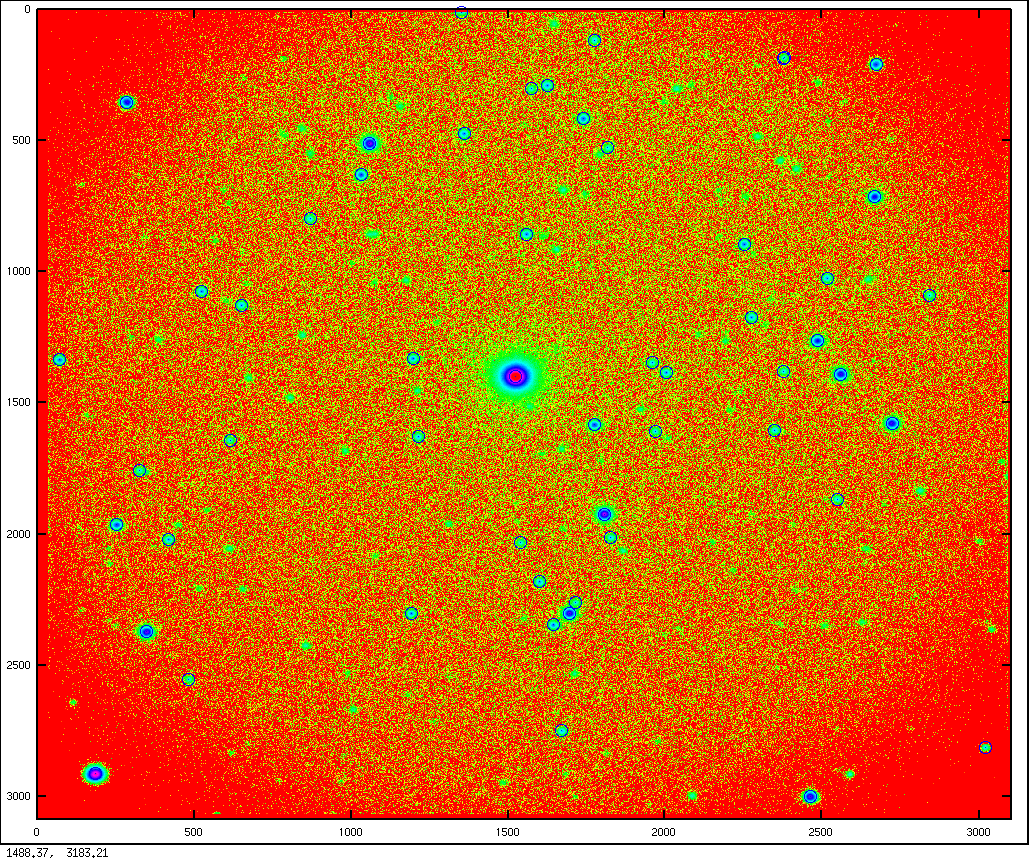
ソースコード
FITSファイルの読み取り:
function [image header] = fits_read(filename) % % FITS- % y ! % ( flipdim, ) % % : % read_fits_image ( fits) % image = []; printf("Read file %s ... ", filename); fflush(1); % , : [ sem ] = stat(filename); if(e != 0 || !S_ISREG(s.mode)) printf("No such file!\n"); fflush(1); return; endif [ image header ] = read_fits_image(filename); if(!isempty(image)) image = flipdim(image',1); % , printf("OK!\n"); else printf("Bad image!\n"); endif fflush(1); endfunction
オブジェクトの中心の計算:
function [ xc, yc ] = find_centers(Img, treshold) % [ xc, yc ] = find_centers(Img, treshold) % Img treshold % xc, yc - % tmp = zeros(size(Img)); mm = mean2(Img) + std2(Img)/4; % tres1 = max(mm, treshold); printf("\nTreshold: %g\n", tres1); fflush(stdout); tmp(find(Img > tres1)) = 1; tmp = medfilt2(logical(tmp)); [ Labels, Nlabels ] = bwlabel(tmp); if(Nlabels < 1) printf(stderr, "\nError! There's no spots!!!\n\n"); return endif [yy, xx] = ndgrid(1:size(Img,1),1:size(Img,2)); xc = []; yc = []; for i = [1 : Nlabels] idxs = find(Labels == i); Is = sum(Img(idxs)); xc = [ xc sum(Img(idxs) .* xx(idxs)) / Is ]; yc = [ yc sum(Img(idxs) .* yy(idxs)) / Is ]; end endfunction
オブジェクト番号Nに対するオブジェクトの座標の計算:
function coords = find_tree(xc, yc, N) % % coords = find_tree(xc, yc, N) % , xc yc, % N . % , - % , - . % if(size(xc, 1)) == 1 % , xc = xc'; endif if(size(yc, 1)) == 1 yc = yc'; endif if(size(xc) != size(yc) || N > size(xc, 1)) % coords = []; endif xn = xc(N); yn = yc(N); % N- Dx = xc - xn; Dy = yc - yn; % N- R = sqrt(Dx.^2+Dy.^2); % Phi = atan2(Dy,Dx)*180/pi; % coords = [R Phi]; endfunction
特定の画像のオブジェクトのすべての相対座標のセットを作成します。
function [Tree xc yc] = get_tree(treshold, i) % % [Tree xc yc] = get_tree(treshold, i) % % : % treshold - % i - % : % Tree - , % * - % * - % * - % xc, yc - % % : % fits_read % find_tree % find_centers % Tree = []; xc = []; yc = []; name = sprintf("object_%04d.fit", i); II = fits_read(name); if(isempty(II)) return; endif printf("Find centers of %s ... ", name); fflush(1); [xc, yc] = find_centers(II, treshold); for j = 1:size(xc,2) Tree(:,:,j) = find_tree(xc, yc, j); endfor printf("done (%d vectors)!\n", size(Tree, 1)); endfunction
2つの画像上のオブジェクト番号の対応を取得する:
function coord_indexes = find_cluster_c(CC, CC1, dR, dPhi) % % coord_indexes = find_cluster_c(CC, CC1, dR, dPhi) % CC CC1 % : % CC, CC1 - % dR - R ( |r1-r0| < dR, , r1 == r0) % dPhi - % : % coord_indexes - [1 2; ...] % Ncc = size(CC, 3); Ncc1 = size(CC1, 3); % - Cluster = []; % : - , 1, 2, for jj = 1 : Ncc % Nnear = []; % , - PhiMed = []; % r0 = CC(:,1,jj); phi0 = CC(:,2,jj); for ii = 1 : Ncc1 % r1 = CC1(:,1,ii); phi1 = CC1(:,2,ii); points = {}; % ( 1; 2) dphi_s = []; % , for i = 1:size(r0); % d = abs(r1-r0(i)); % idx = find(d < dR); % r if(isempty(idx)) continue; endif; % - points = [ points; {i, idx} ]; % endfor for i = 1:size(points, 1) dphi = abs(phi1(points{i,2}) - phi0(points{i,1})); dphi_s = [dphi_s; dphi]; endfor if(isempty(dphi_s)) continue; endif; dphi = median(dphi_s); % 2 1 n = size(find(abs(dphi_s-dphi)<dPhi), 1); Nnear = [ Nnear, n ]; % PhiMed = [ PhiMed, dphi ]; endfor idx = find(Nnear == max(Nnear))(1); % , jj- Cluster = [ Cluster; Nnear(idx) jj idx PhiMed(idx) ]; endfor % n = max(Cluster(:,1)); % idx = find(Cluster(:,1) == n)(1); % first = Cluster(idx, 2); % 1 second = Cluster(idx, 3); % -//- 2 Phi = Cluster(idx, 4); % 2 1 r0 = CC(:,1,first); phi0 = CC(:,2,first); r1 = CC1(:,1,second); phi1 = CC1(:,2,second); coord_indexes = []; for i = 1:size(r0); % d = abs(r1-r0(i)); % idx = find(d < dR); % r if(isempty(idx)) continue; endif; % - dphi = abs(abs(phi1(idx) - phi0(i)) - Phi); if(size(idx, 1) != 1) % n = find(dphi == min(dphi))(1); % idx = idx(n); dphi = dphi(n); endif if(dphi > dPhi) continue; endif; % - coord_indexes = [ coord_indexes; i idx ]; endfor endfunction
最初の画像の番号付けに従って、すべての画像のオブジェクトの座標の配列を取得します。
function [XY] = get_centers(i0, i1, treshold, dR, dPhi) % % [XY] = get_centers(i0, i1, treshold, dR, dPhi) % X,Y % % : % i1, in - % treshold - % dR, dPhi - ( ) % : % X, Y - % % - % - % % : % get_tree -> fits_read, find_tree, find_centers % find_cluster_c % n = 1; % + X,Y i_start = i0; % CS = []; printf("\nimage 1\n", i); do [CC xc yc] = get_tree(treshold, i_start); im1 = i_start; i_start++; until(!isempty(CC) || i_start > i1) X = xc'; Y = yc'; % - Counters = zeros(size(X)); % for i = i_start:i1 [CC1 xc1 yc1] = get_tree(treshold, i); if(isempty(CC1)) continue; endif printf("\nimage %d, ", ++n); % indexes = find_cluster_c(CC, CC1, dR, dPhi); printf("%d points\n\n", size(indexes, 1)); % : X(indexes(:,1),n) = xc1(indexes(:,2)); Y(indexes(:,1),n) = yc1(indexes(:,2)); % Counters(indexes(:,1))++; endfor % , idx = find(Counters != n-1); X(idx,:) = []; Y(idx,:) = []; endfunction
回転中心の取得:
function [Xc Yc] = matr_center(X, Y) % % [Xc Yc] = matr_center(X, Y) % , % : % X, Y - ( get_centers) % : % Xc, Yc - % Xc = []; Yc = []; imax = size(X,2); for i = 1:imax-1 for j = i+1:imax % X0 = X(:,i)'; X1 = X(:,j)'; Y0 = Y(:,i)'; Y1 = Y(:,j)'; % ( - ) vec0X = X0 - mean(X0); vec0Y = Y0 - mean(Y0); vec1X = X1 - mean(X1); vec1Y = Y1 - mean(Y1); % , %phi0 = atan2(vec0Y, vec0X); phi1 = atan2(vec1Y, vec1X); %% 2, -pi+a -> pi-b %phi0(find(phi0<0)) += 2*pi; phi1(find(phi1<0)) += 2*pi; %dphi = median(phi1 - phi0); % %R = [cos(dphi) -sin(dphi); sin(dphi) cos(dphi)]; % %RR1 = R * [vec0X;vec0Y]; % , 0 %dR = sqrt((vec1X-RR1(1,:)).^2+(vec1Y-RR1(2,:)).^2); % %idx = find(dR < median(dR)+std(dR)); % %if(size(idx,2) < 3) % %printf("Image %d: too much bad data\n", i); %continue; %endif %X0 = X0(idx); X1 = X1(idx);Y0 = Y0(idx); Y1 = Y1(idx); % A = [X1;Y1;ones(size(X1))]/[X0;Y0;ones(size(X1))]; % CRDS = (eye(2)-A(1:2,1:2)) \ A(1:2,3); Xc = [Xc CRDS(1)]; Yc = [Yc CRDS(2)]; % endfor endfor Xmed = median(Xc) Ymed = median(Yc) endfunction
同じですが、McKeinアソシエイツメソッドによるものです。
function [Xc Yc] = matr_center_notmine(X, Y) % % [Xc Yc] = matr_center(X, Y) % , % : % X, Y - ( get_centers) % : % Xc, Yc - % Xc = []; Yc = []; imax = size(X,2); for i = 1:imax-1 for j = i+1:imax % X0 = X(:,i)'; X1 = X(:,j)'; Y0 = Y(:,i)'; Y1 = Y(:,j)'; % ( - ) vec0X = X0 - mean(X0); vec0Y = Y0 - mean(Y0); vec1X = X1 - mean(X1); vec1Y = Y1 - mean(Y1); phi0 = atan2(vec0Y, vec0X); phi1 = atan2(vec1Y, vec1X); % 2, -pi+a -> pi-b phi0(find(phi0<0)) += 2*pi; phi1(find(phi1<0)) += 2*pi; dphi = median(phi1 - phi0); % R = [cos(dphi) -sin(dphi); sin(dphi) cos(dphi)]; % % v v = median(R * [X0; Y0] - [X1; Y1], 2); % CRDS = (eye(2)-R) \ v; %printf("Center: (%g, %g)\n", CRDS(1), CRDS(2)); Xc = [Xc -CRDS(1)]; Yc = [Yc -CRDS(2)]; % endfor endfor Xmed = median(Xc) Ymed = median(Yc) endfunction