Clever Geek Handbook

WiMaxとLTEがOFDMを使用する理由





OFDMは、直交周波数分割多重化の略です。 ロシアの文献には、原則として1つの意味を持ついくつかの異なる翻訳があります。OFDMは、直交サブキャリアによる多重化メカニズム（多重化）です。









この記事では、OFDMメカニズムの長所と短所について説明します。 物理的および数学的な位置から機能する原理が考慮されます。 この記事には、幅広い読者に資料を理解するために必要な放射線物理用語の入門説明が含まれています。













イラスト：18、文字：27 399、コード行：99。











最新の電気通信の有線および無線規格の仕様は、OFDMテクノロジーを使用してますます見られています。 無線システムのアーキテクチャの時間によって決まる要件により、高い人気が確保されます。 OFDMメカニズムには、時間の傾向を満たす多くのプロパティがあります。 前世紀の60年代に開発されたこの技術は、ごく最近になって使用できるようになりました。









ロシア語には十分な量のOFDM関連資料があります。 たとえば、Habrでは、 Yotaの優れた記事を読むことができます。 一部のソースのリストは、記事の最後に記載されています。









資料のプレゼンテーションは、さまざまなレベルのトレーニングを受けた読者向けに設計されています。 したがって、共通の言語を話すために、記事の前半には入門資料が含まれています。 経験豊富な読者であれば、記事の後半に直接アクセスできます。ここでは、OFDMについて直接説明します。 タイトルで提起された質問への回答にのみ興味がある人のために、以下の最初の数段落のみを読むことができます。









WiMaxとLTEがOFDMを使用する理由



その秘密はテクノロジーの特徴にあり、主なプラス面とマイナス面を簡単に強調できます。









長所





短所





すべての欠点にもかかわらず、OFDMは大都市で動作する最新のネットワークのアーキテクチャにとって優れたソリューションです。 技術の進歩と市場のダイナミクスにより、メーカーは常に既存の技術の改善を迫られています。 その結果、さまざまなOFDM修正をベースとして使用するデバイスが登場します。 ただし、中核とその中に定められた原則は同じままです。 この記事では、OFDMテクノロジーの機能の表面的な基礎について説明します。









ステップ1.スペクトルについて



次の図に示す信号を考えてください。

















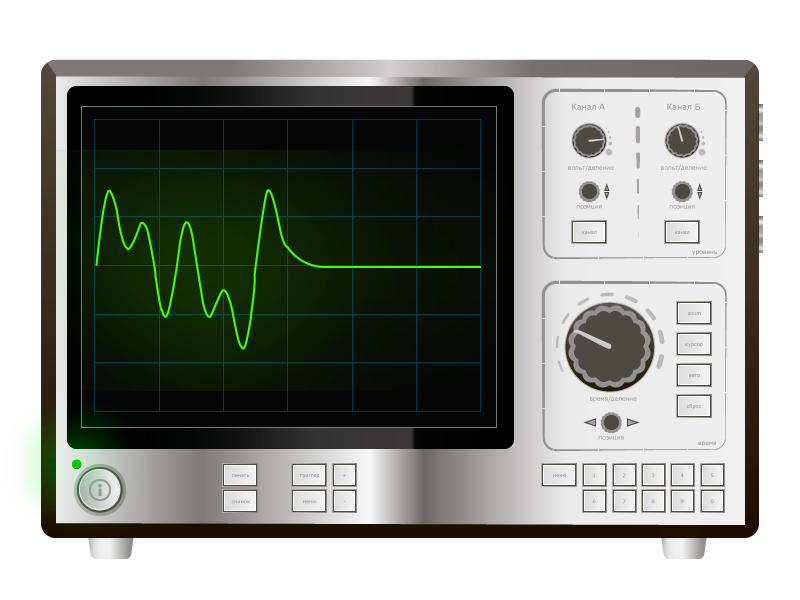
便宜上、信号の1周期（1反復サイクル）のみが指定されています。 信号は、電気回路のある点での電圧の時間変化です。 このような変更の作成、送信、および受信は、ラジオエレクトロニクスの本質です。









電圧の経時変化を見ると、多くの結論が導き出されます。 これが、たとえばセンサーからの信号である場合、グラフは測定値のダイナミクスを示します。 ただし、現代の無線工学はスペクトルの言語を話す可能性が高くなります。 次の図は、この概念を理解するのに役立ちます。

















オシロスコープで観測された信号（前の図）は、基本振動に分解できます。 さらに、物理的に観測可能な信号は、このような分解を受ける可能性があります。 基本振動は、正弦関数または余弦関数によって数学的に記述された信号を意味すると理解されています。 実際、サインとコサインは本質的に同じ信号であり、時間的にわずかにシフトします。









これらすべての基本信号をワイヤに沿って同時に実行すると、測定中に最初の「複雑な」信号を確認できます。









サインのような関数は高調波と呼ばれます。 したがって、それらは「複雑な」信号の一部として高調波と呼ばれることがよくあります。 各信号には、固有の高調波のセットがあります。 この高調波のセットは、信号スペクトルと呼ばれます 。 信号の高調波の研究は、スペクトル（調和）分析によって実行されます。









ステップ2.数学的波形



エンジニアと研究者は、比較的単純な数学を使用して、信号とそのスペクトルを記述します。 図に示すように、複雑な信号はより単純な信号の合計として記録されます。

















すでに述べたように、各高調波は、正弦の数学関数によって記述される単純な振動です。 サインの前の係数は「振幅」と呼ばれ、引数は「位相」と呼ばれます。 フェーズは2つの数値の合計です。 最初の項は時間と循環周波数の積であり、2番目の項は初期位相です。 検討中の複素信号の高調波の初期位相はゼロです。これは明確にするために選択されました。 通常のフェーズと初期フェーズを混同しないように、「完全フェーズ」と呼ばれます。 「フェーズ」、「初期フェーズ」、「振幅」、「周期的（円形）周波数」、および「関数」という用語の説明は、数学の教科書にあります。 文献で「フェーズ」という言葉が出てきた場合、これは通常、特定の状態、つまり 「フェーズ」=「状態」。 この場合、高調波信号の全位相は、特定の時間における関数の特定の状態を表します。 言い換えると、高調波変化の法則（正弦）とその現在の状態（完全な位相）を知っていれば、高調波の現在の値が何であるかを知ることができます。









サインを使って録音することは必ずしも便利ではありません。 エンジニアリングの実践では、通常、出展者の形で記録の形になります。 これにはいくつかの利点があります。 詳細は文献に記載されています。 指数形式で記述する場合、複素数が使用されることに注意してください。 これらの数の理論は、想像上の単位の概念と密接に関連しています。 指数形式は、上の図に示すように、回転ベクトルとして明確に表すことができます。 平面内で周期的な周波数で回転し、一方の軸に実数が、他方の軸に虚数がプロットされます。 これらはすべて、数学および工学の文献でさらに詳しく読むことができます。









ステップ3.フーリエ変換



数学では、信号とそのスペクトルを接続する非常に重要な変換があります。 これはフーリエ変換と呼ばれます。 明確にするために、写真を見てみましょう。

















フーリエ変換には2つの式があります。写真では、フェルトペンで囲まれています。 直接変換は信号をスペクトルに変換し、逆変換はスペクトルを信号に変換します。 式では、変換のタイプに応じて、スペクトルまたは信号のいずれかを記述する関数を置き換える必要があります。 数式がこのような形式を持っている理由については、数学の本で再び読むことができます。 同じ場所で、フーリエ変換を適用できる場合とできない場合を理解できます。 また、申請できない場合はどうすればよいのでしょうか。ただし、スペクトルを取得する必要があります。 ほとんどの実世界の信号では、フーリエ変換は有効ですが、残りのケースは考慮されません。









減衰指数として写真に描かれている信号を直接変換した後、そのスペクトルを取得します。 一般的な場合、スペクトルは複素数です。 前述のように、指数と記録信号の数と形式について説明しました。 この形式では、振幅と初期位相の2つの信号パラメーターが表示されます。 信号が複雑な場合、複数の高調波で構成され、各高調波には独自の振幅と位相があります。 数学的には、これは簡単です。 信号の指数記録では、通常の振幅と初期位相の数の代わりに、周波数の振幅と周波数の初期位相の関数が書き込まれます。 このような依存関係により、出力で直接フーリエ変換が行われます。 その結果、信号の振幅スペクトルと位相スペクトルが分離されます。 上の画像はこれらのスペクトルを示しています。 それらは多数の倍音で構成されているため、それらを描くことは視覚的ではありません。 通常、 封筒のみが表示されます。









複雑な信号は、サインやコサインだけでなく、ちなみに指数関数にも配置できます。 他のクラスの「基本」関数があり、その合計の形で信号を表すことができます。 クラス内のこれらすべての関数には、共通のプロパティ「直交性」があります。 または言い換えれば-垂直性。 したがって、2つの直交関数を取り、それらが関数ではなくベクトルであると想像すると、それらの間には90度の角度があります。 これら2つの関数を乗算すると、ゼロになります。 これは単なるゼロではなく、このゼロの背後には明確な意味があります：直交信号間の相互エネルギーはゼロ、つまり それらは相互に作用しません。









ステップ4.高速フーリエ変換



アナログフーリエ変換を生成する手法には、十分な数の手法があります。 光速でこれを即座に行うシステムもあります 。 ただし、ディスクリート信号が使用されるデジタル技術では、多くの場合、アナログコンバーターの使用は適切ではありません。 その結果、信号スペクトルをすばやく取得できる数学的アルゴリズムは非常に人気があります。 このアルゴリズムは高速フーリエ変換（FFT）と呼ばれ、その簡略化された回路を次の図に示します。

















  1. 高速フーリエ変換は、離散信号で機能します。 離散信号は、アナログ信号の値から一定期間後に取得される一連の数値です。
  2. 信号の離散化は、特定の規則に従って実行されます。 これは別の議論のトピックです。 誰も気にせず、コテルニコフ（シャノン）の定理に関する記事や本を検索できます 。 離散信号のセットからの各数値がバイナリコードとして表される場合、デジタル信号が取得されます。 最終的に、期間Tのアナログ信号から、N個の数値（ポイント）の配列が取得されます。
  3. 離散フーリエ変換のタスクは、信号サンプルの配列からスペクトル番号の配列を取得することです 。 これらの数値は、上記の直交分解関数の係数です。 アナログ変換からフーリエ変換の離散形式を取得するのは非常に簡単です。 最終ビューは写真（番号3）で見ることができます。
  4. この瞬間から、高速フーリエ変換アルゴリズムが直接始まります。 このアルゴリズムは、サイズが2のべき乗の配列である場合に最適に機能します。 したがって、レポートの数が2の累乗と異なる場合、切り上げて欠落している要素をゼロ値で埋めることにより、レポートの数を増やします。 シーケンス全体は、偶数カウントと奇数カウントの2つの部分に分かれています。 結果のシーケンスの長さはN / 2です。
  5. N / 2までのサンプルでは、​​図に示されている式（5番の下）が有効であることが単純な数学的変換によって示されます。
  6. サンプルの後半の値の場合：N / 2からNまで、単純な式に移動することもできます。 これは、係数Cの周期性に基づいて取得されます。その結果、任意の係数Cの完全な式は、図（番号6の下）に示すように記述できます。
  7. この形式では、アルゴリズムにより速度がいくらか向上します。 離散信号（図の式3）からスペクトルの「正面」を取得する場合、これには複素数による乗算のN回の演算とN回の加算が必要になります。 そして、これはただ一つのスペクトル係数を取得することであり、Nのみがあります。最終的に、N 2の乗算とN 2の加算を実行するために必要なすべての係数を取得します。 上記で取得した式（図の式番号6）を使用する場合、2（N / 2） 2 + Nの乗算が必要です。 これはほぼ半分のサイズです。 各シーケンスを最大2要素の配列に分割することにより、図（7の下）に示すように、計算の数をさらに減らすことができます。 この手法により、約N log 2 Nの乗算演算が行われます。 たとえば、1024サンプルの場合、乗算操作の数は100倍に減少します！ これにより、テクノロジーにおけるフーリエ変換の適用が大幅に簡素化されます。




ステップ5.変調



オシロスコープで別の複雑な信号を検討します。

















これは振幅変調されたアナログ信号です。 私たちは何について話しているのですか？ たとえば、ヘッドセットのマイクから「無線で」電話に情報を転送する場合、それを解決するには、まず音声（音）を読み、それを何らかの方法で電話に転送する必要があります。 現在、ある種の問題のように、彼らはすでに何らかの形で最適な多くのエレガントなソリューションを持っています。 明確にするために、例を検討できます。

















図は、信号変調手順の本質を簡単に説明しています。 基本的に、変調の概念は、別の信号（低周波数）に応じて、ある信号（高周波数）のパラメーターの変化に関連付けられます。 特定の状況で最適な方法で信号を送信できるようにするさまざまな変調方式（タイプ）がありますが、すべては信号の振幅、周波数、または初期位相のいずれかを変更することになります。









低周波信号には情報が含まれています。 たとえば、私たちのケースでは、簡単にするために、これはいくつかのシングルトーンサウンドです。 単純な信号。 高周波信号のエンベロープは、この信号の振幅に応じて変化します。 高周波信号は、情報を運ぶ（運ぶ）という意味で「キャリア」と呼ばれます。 変調手順なしで情報信号を送信できる場合があります。 実際には、信号は何らかの物理的媒体を介して、さらには干渉の存在下でも送信されます。 この場合、信号を正常に送信するために、変調が適用されます。









いくつかの計算を行うことにより、変調の利点を確認できます。 「空気中」の信号は、主に波が伝播する電磁場を使用して送信されることが知られています。 アンテナによる放射波と受信波。 波は"波長"によって特徴付けられます。 この値は波の周波数の逆数であり、送信信号の周波数に対応します。 明らかに、周波数が高いほど、波長は短くなります。 アンテナの寸法は、使用する波長によって異なります。 したがって、信号周波数が高いほど、アンテナは小さくなります。 たとえば、5オクターブの音「To」をヘッドセットから電話機に転送しようとすると（これは4186.0 Hzです）、アンテナの長さは約18 kmになります。 また、Bluetooth仕様の周波数（約2.4 GHz）を使用する場合、アンテナのサイズはわずか3 cmになります。もちろん、推定値は推定されますが、結果から変調の利点を検証できます。









既に述べたように、多数の変調方式があります。 ただし、デジタル変調方式はアナログとは少し異なり、上記で部分的に説明しました。 したがって、それらに注意を払う必要があります。 アナログ回路の場合と同様に、ジャンプ、パラメーターの変更を除いて、基本的に3つのパラメーター、つまり周波数、位相、振幅の変更がすべて行われます。 この種の変調は、 「操作」と呼ばれます（eng。Shiftキー）。 下の図は、振幅（ASK）、周波数（FSK）、および位相（PSK）の操作スキームを示しています。

















現代の通信システムでは、さまざまな振幅操作QAM（直交）が非常に人気を集めています。 その本質は、2つの単純な信号の合計から信号を合成することであり、その間の位相差は90度です（これらは直交します）。 これらの単純な信号の振幅は離散的に変化し、最終的に振幅と位相の両方が同時に変化する離散的な信号を形成します。 可能性のあるすべての状態を位相面に描くと便利です。 上の図では、このようなプレーンが16-QAM変調用に示されています。 16ビットの状態は、4ビットの情報に対応する単一のQAM変調シンボルでエンコードできます。 ちなみに、このような考慮事項に基づいて-位相操作は特別なケースと見なすことができます。 たとえば、QPSK操作は4-QAMと呼ばれる場合があります。 したがって、操作スキームを変更することにより、データフローレートを増減できます。 ただし、速度を上げるには、ノイズ耐性を犠牲にする必要があります。 さまざまな通信チャネルで、「ゴールデンミーン」が使用されます。 QAMの否定できない利点に加えて、欠点もあります。 考慮される変調方式は、多くの場合、純粋な形では使用されません。 これらはすべて現代の通信システムに関する本で読むことができます。









ステップ6.多重化



通信システム開発者は、時間、空間、周波数、コードなど、限られた伝送媒体リソースという絶え間ない問​​題に直面しています。 したがって、1人のユーザーまたは複数のユーザーに対して複数のデータストリームを転送する必要がある場合、メディアへの複数アクセスの問題を解決する必要があります。 つまり、既存の条件での通信をより適切に編成するために、フローを圧縮するか、そのようなアルゴリズムを設計する必要があります。 文献では、この問題は多重化、シール、および多重アクセス（MAC）と呼ばれています。









フローの空間的な分離は 、問題に対する比較的単純な解決策と見なすことができます。 この分離の例として、MIMOテクノロジー（英語の複数入力複数出力）があります。これは、現代のすべてのネットワーク標準に​​広く実装されています。 一番下の行は、送信と干渉しないように間隔を空けた複数のアンテナを使用することです。 「無線」でのデータ交換の速度の記録は、主にこの技術のために破壊されています。 また、空間的な分離の最も単純な例は、送信機の電力の制限またはアンテナ放射パターンの適応的な変更です。 これとテクニックのすべての複雑さは、専門の文献に記載されています。









より一般的なのは、 周波数分割多重化またはFDM（周波数分割多重化）の手法です。 この手法のおかげで、膨大な数のデバイスが1つの領域で動作します。 次の図は、圧縮の原理を示しています。

















この図は、異なる色で示されるフロー間で時間周波数とエネルギーリソースがどのように分配されるかを示しています。 マイナス面の1つは、相互干渉を排除するためにストリーム間に周波数ギャップを残す必要があることです。これは、周波数リソースを最適な方法で使用しません。









より柔軟なのは、 一時的な圧縮またはTDM（時分割多重）の手法です。 以下は彼女のチャートです。

















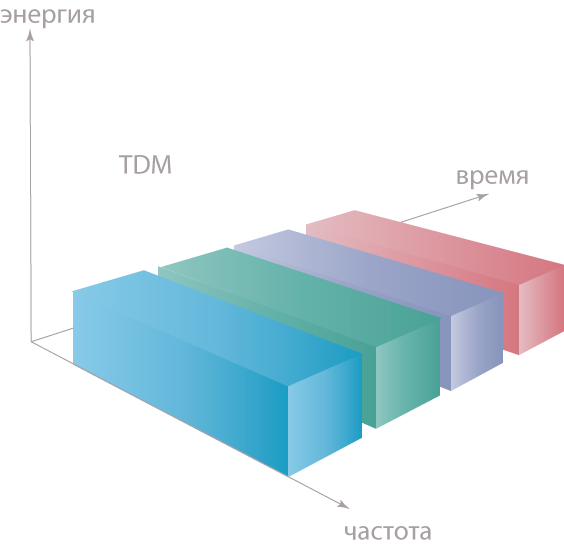
この場合、トランスミッタは1つの周波数のみを使用しますが、各ストリームは独自の時間間隔を使用します。 この手法は、受信機と送信機の間の同期を非常に要求します。 TDMは、動的に変化するフローに便利です。たとえば、フロー（加入者）がトラフィックを増やす必要がある場合、間隔をより信頼性のあるものにするには十分です。 TDMを使用する最も有名な標準はGSMです。









コード圧縮技術またはCDM（Code Division Multiplexing）に注意してください。 彼女は面白いチャートを持っています。

















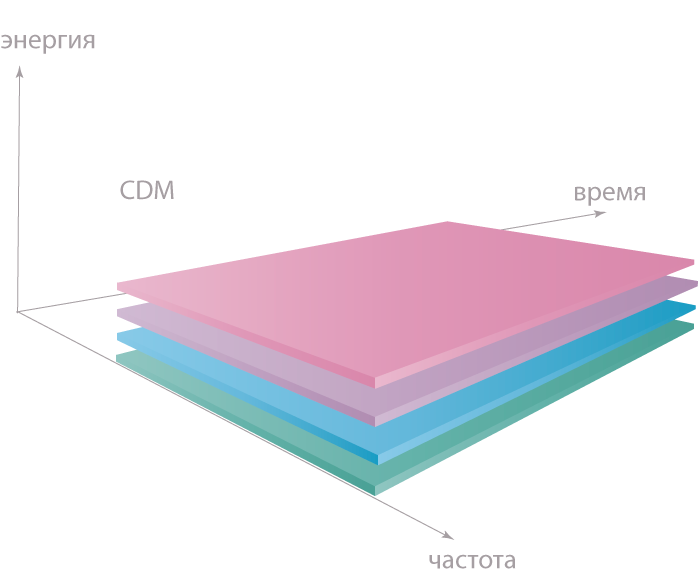
ストリームは同じ時間周波数間隔で共存します。 各ストリームのエンコードには特別なコードが使用されます。 CDMコードは、元のシーケンスのシンボルが分解される直交信号です。 これを行うことができる理由は、上記で述べた。 これは、スペクトルを広げる手法の1つです。 ノイズのような信号とスペクトル拡大技術は、電気通信の興味深い分野です。 興味がある人は、文献の追加資料を見ることができます。









CDMテクニックにはさまざまな変更があります。 たとえば、CDMとFMDの混合はFHSS（周波数ホッピングスペクトラム拡散）を提供し、TDMではTHSS技術（タイムホッピングスペクトラム拡散）を提供します。 独自の特性を備えた変更により、CDMアプリケーションの幅広い視野が広がります。 たとえば、FHSSはBluetoothで使用されます。 CDMおよびFDMのもう1つの派生物は、この記事で検討するOFDM方式です。









より正確な用語については、いくつかのユーザーの環境への多重アクセスを目的とする圧縮技術は、英語の文献では多重アクセスと呼ばれているため、そのような技術はFDMA、TDMA、CDMA、OFDMAなどと呼ばれることを明確にする必要があります 他の圧縮および多元接続技術は、追加の書籍で見つけることができます。









ステップ7. OFDM



OFDM技術では、周波数範囲はサブキャリア（追加のキャリア）間で均等に分割され、その数は数千に達することがあります。 各送信ストリームには、このようなサブキャリアがいくつか割り当てられます。 各ストリームはN個のサブキャリアに分割されます。 サブキャリアは互いに直交しています。 この機能は、OFDM技術の多くの利点を定義します。 直交性の概念の意味は上記で説明されました。 明確にするために、次の図をご覧ください。

















OFDMテクノロジーを使用する一般的な標準は、 DVBデジタルテレビ放送システムです。 ちなみに、このシステムはロシアのデジタルテレビの標準として使用されます。 DVB-T地上波放送の例、またはその修正を使用して、OFDM信号を生成する機能と原理を検討します。







  1. DVB-Tでは、サブキャリア間の分離前の信号は、ノイズ耐性を改善するためにさまざまなエンコーダーによってプリコーディングされます。 標準の機能には触れません。 OFDM形成の詳細だけを見てみましょう。

  2. DVB-T信号は、8 MHz（7、6 MHz）の帯域を占有します。 この帯域はサブキャリア間で分割されます。 サブキャリア間の信号スペクトルの距離は、1つのOFDMシンボルの持続時間に反比例します。







  3. 干渉に対処するために、OFDMにはガードインターバルが含まれています。 これができるのは 高速データフローはサブキャリア間で分割され、各サブフローのサブフローレートは初期のサブフローレートよりも低くなります。 このため、メイン信号を干渉から保護する時間の長さを選択できます。 このガードインターバルの期間は、OFDMシンボルの期間の1 / 4、1 / 8、1 / 16、または1/32になります。 この図は、一時的なガードインターバルを使用する原理を説明しています。











    , () , , , . , . . , OFDM . .
  4. , . . , OFDM , , QPSK, 16-QAM 64-QAM. , () .
  5. OFDM , . . , . , (IFFT) . , . . OFDM.











    , , QAM . , «» . .
  6. , FFT/IFTT c , OFDM . , DVB-T 8k 2k, : 8000 2000 . 8192 (2 13 ) 2048 (2 11 ), , 1705 6817, . OFDM DVB-T MatLAB :




  1. %DVB-T 2K Transmission
  2. % 8 MHz
  3. %2K
  4. clear all ;
  5. close all ;
  6. %DVB-T
  7. Tu=224e-6; % OFDM
  8. T=Tu/ 2048 ; %
  9. G= 1 / 4 ; % 1/4, 1/8, 1/16, 1/32
  10. delta=G*Tu; %
  11. Ts=delta+Tu; % OFDM
  12. Kmax= 1705 ; %
  13. Kmin= 0 ;
  14. FS= 4096 ; %IFFT/FFT
  15. q= 10 ; %
  16. fc=q* 1 /T; %
  17. Rs= 4 *fc; %
  18. t= 0 : 1 /Rs:Tu;
  20. %
  21. M=Kmax+ 1 ;
  22. rand ( 'state' , 0 ) ;
  23. a=- 1 + 2 * round ( rand ( M, 1 ) ) .' +i * ( - 1 + 2 * round ( rand ( M, 1 ) ) ) .';
  24. A= length ( a ) ;
  25. info= zeros ( FS, 1 ) ;
  26. plot ( info ) ;
  27. info ( 1 : ( A/ 2 ) ) = [ a ( 1 : ( A/ 2 ) ) .' ] ;
  28. info ( ( FS- ( ( A/ 2 ) - 1 ) ) :FS ) = [ a ( ( ( A/ 2 ) + 1 ) :A ) .' ] ;
  30. %
  31. carriers=FS.* ifft ( info,FS ) ;
  32. tt= 0 :T/ 2 :Tu;
  33. figure ( 1 ) ;
  34. subplot ( 211 ) ;
  35. stem ( tt ( 1 : 20 ) , real ( carriers ( 1 : 20 ) ) ) ; %
  36. subplot ( 212 ) ;
  37. stem ( tt ( 1 : 20 ) , imag ( carriers ( 1 : 20 ) ) ) ; %
  38. figure ( 2 ) ;
  39. f= ( 2 /T ) * ( 1 : ( FS ) ) / ( FS ) ;
  40. subplot ( 211 ) ;
  41. plot ( f, abs ( fft ( carriers,FS ) ) /FS ) ;
  42. subplot ( 212 ) ;
  43. pwelch ( carriers, [ ] , [ ] , [ ] , 2 /T ) ;
  45. %
  46. L = length ( carriers ) ;
  47. chips = [ carriers.';zeros ( ( 2 *q ) - 1 ,L ) ] ; %
  48. p= 1 /Rs: 1 /Rs:T/ 2 ;
  49. g= ones ( length ( p ) , 1 ) ;
  50. figure ( 3 ) ;
  51. stem ( p,g ) ;
  53. dummy= conv ( g,chips ( : ) ) ; %
  54. u= [ dummy ( 1 : length ( t ) ) ] ; %
  55. figure ( 4 ) ;
  56. subplot ( 211 ) ;
  57. plot ( t ( 1 : 400 ) , real ( u ( 1 : 400 ) ) ) ;
  58. subplot ( 212 ) ;
  59. plot ( t ( 1 : 400 ) , imag ( u ( 1 : 400 ) ) ) ;
  61. figure ( 5 ) ;
  62. ff= ( Rs ) * ( 1 : ( q*FS ) ) / ( q*FS ) ;
  63. subplot ( 211 ) ;
  64. plot ( ff, abs ( fft ( u,q*FS ) ) /FS ) ;
  65. subplot ( 212 ) ;
  66. pwelch ( u, [ ] , [ ] , [ ] ,Rs ) ;
  68. [ b,a ] = butter ( 13 , 1 / 20 ) ; %
  69. [ H,F ] = FREQZ ( b,a,FS,Rs ) ;
  70. figure ( 6 ) ;
  71. plot ( F, 20 * log10 ( abs ( H ) ) ) ;
  72. uoft = filter ( b,a,u ) ; %
  74. figure ( 7 ) ;
  75. subplot ( 211 ) ;
  76. plot ( t ( 80 : 480 ) , real ( uoft ( 80 : 480 ) ) ) ;
  77. subplot ( 212 ) ;
  78. plot ( t ( 80 : 480 ) , imag ( uoft ( 80 : 480 ) ) ) ;
  80. figure ( 8 ) ;
  81. subplot ( 211 ) ;
  82. plot ( ff, abs ( fft ( uoft,q*FS ) ) /FS ) ;
  83. subplot ( 212 ) ;
  84. pwelch ( uoft, [ ] , [ ] , [ ] ,Rs ) ;
  86. %Upconverter
  87. s_tilde= ( uoft.' ) .* exp ( 1i * 2 * pi *fc*t ) ;
  88. s= real ( s_tilde ) ;
  89. figure ( 9 ) ;
  90. plot ( t ( 80 : 480 ) ,s ( 80 : 480 ) ) ;
  91. figure ( 10 ) ;
  92. subplot ( 211 ) ;
  93. %plot(ff,abs(fft(((real(uoft).').*cos(2*pi*fc*t)),q*FS))/FS);
  94. %plot(ff,abs(fft(((imag(uoft).').*sin(2*pi*fc*t)),q*FS))/FS);
  95. plot ( ff, abs ( fft ( s,q*FS ) ) /FS ) ;
  96. subplot ( 212 ) ;
  97. %pwelch(((real(uoft).').*cos(2*pi*fc*t)),[],[],[],Rs);
  98. %pwelch(((imag(uoft).').*sin(2*pi*fc*t)),[],[],[],Rs);
  99. pwelch ( s, [ ] , [ ] , [ ] ,Rs ) ;




Guillermo Acosta. :

















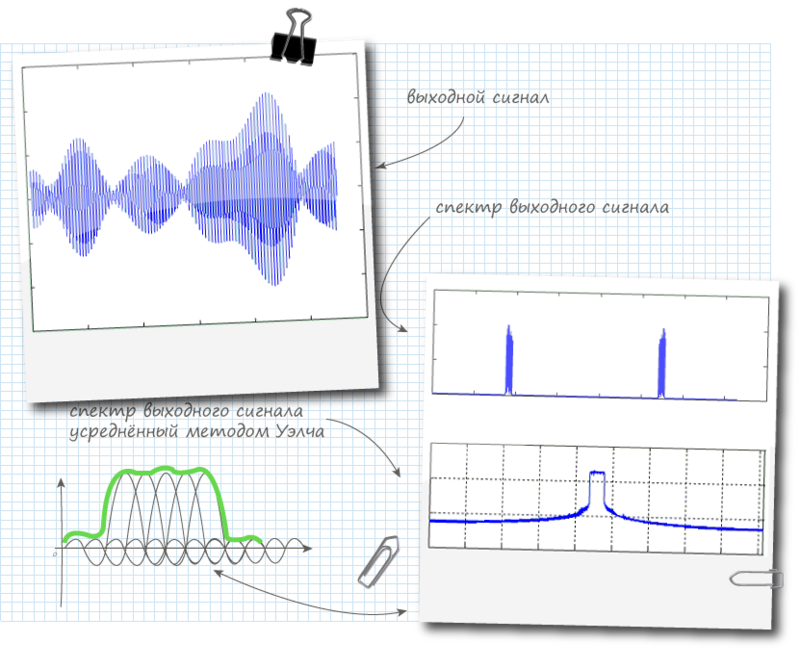
8. OFDM





OFDM, .









  1. COFDM (Coded OFDM). OFDM , . DVB-T , OFDM.
  2. Flash OFDM (Fast low-latency access with seamless handoff OFDM). Flarion Technologies . . . , .
  3. OFDMA . . OFDM .
  4. VOFDM (Vector OFDM). Cisco Systems . MIMO. MIMO-OFDM.
  5. WOFDM（広帯域OFDM）。Shirokoloposnaya修正OFDMを開発LANのWi-株式会社を。変更では、スループットとノイズ耐性の向上が達成されます。主な違いは、キャリア間の周波数間隔が大きいことです。




考慮されたシステムの中で、古典的なOFDMスキームとCOFDMの修正は非常に人気があります。



ステップ9.結論



OFDM. , , , . OFDM, , , , . .









10.



  1. OFDM-Based Broadband Wireless Networks. Design and Optimization. Hui Liu and Guoqing Li
  2. Multi-Carrier and Spread Spectrum Systems. From OFDM and MC-CDMA to LTE and WiMAX. K. Fazel, S. Kaiser
  3. OFDM. Concepts for Future Communication Systems. Hermann Rohling
  4. . .
  5. . . .
  6. . . .
  7. . . .
  8. . . .
  9. . .., ..
  10. MATLAB ( ViruScD ).
  11. ( eucariot ).




PSリソースルールとCreative Commons Attribution 3.0 Unported（CC BY 3.0）の条件に従ってください


More articles:


All Articles