
勝者はモスクワのピーター・ミトリチェフでした。 彼は1万ドルの賞金を受け取りました。 2位はサンクトペテルブルクのユージーンカプンが撮影し、5000ドルを受け取りました。 3位はサンクトペテルブルク出身のミハイルドヴォルキンで、賞金は3000米ドルです。 皆さん、おめでとう、彼らが引き続き成功することを願っています!
この記事では、最終ラウンドのタスクを分析します。
タスクの完全な説明は、 ここにあります 。
タスクA.クロック転送
この問題では、いくつかの都市で時計を設定するためのルールが設定され、すべての都市の居住者の合計の不便を見つける必要がありました.1組の都市の不便はこれらの都市の時差として定義され、これらの値は年間のすべての時間で合計する必要がありました。
まず、指定された都市の1つが首都であり、時間は首都で翻訳されないことに注意してください。 したがって、メトロポリタン時間を参照の「絶対スケール」として選択し、それを使用してすべてのイベントの時間を示すのが便利です。 まず、入力ファイルで指定されたすべてのクロック変換を実行し、クロック変換ごとにその時間を絶対スケールで決定します。 現在、各クロック転送は3つの数値によって特徴付けられています。
•発生した絶対スケールの時間、
•乗り換えが行われる都市、
•クロック転送の量。
次に、絶対スケールで発生する順序でイベントを検討します。 前のイベントから現在のイベントまでずっと、この国の不便さは一定でした。
特定の都市での時間の変化の結果として、その国の不便さがどのように変化したかを見てみましょう。 市が首都に対してi時間シフトしているとします。 より小さな時間シフトを持つ都市の合計シフトをS、その数をLとしましょう
特定のシフトセグメントの都市の合計時間シフトをすばやく計算し、セグメント内の都市の数を計算するには、たとえば、セグメントのツリーまたはフェンウィックツリーを使用できます。
問題B.逆タートル問題
この問題では、特定の数kに対して、左上から右下のセルへのパスの数が右と下にのみ移動できる場合、kと等しい迷路を構築する必要がありました。
以下に注意してください。 左上から右下に到達する方法の数がそれぞれaとbに等しい2つの迷路があるとします。
次に、図に示すように、それらを並列に配置して、左上から右下のセルにa + bの方法で迷路を取得し、それらを連続して配置します-abパスの迷路を取得します。
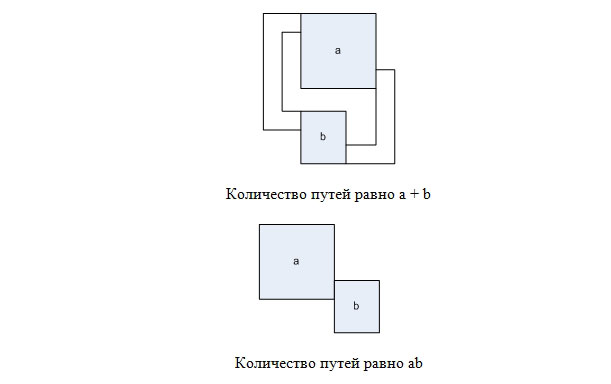
空の2×2迷路には2つのパスがあり、1×1迷路には1つのパスがあることに注意してください。 したがって、数値kを2進数に展開し、説明した方法を使用すると、左上のセルから右下のセルまでのパスがk個ある迷路を取得できます。
このようなk = 19の迷路の例を図に示します。
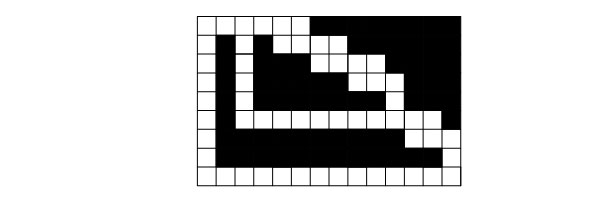
番号kの放電ごとに、水平方向に5つのセルが必要であり、2 60 > 10 18であるため、上記のスキームでは、問題の必要に応じて、サイズが300×300以下のラビリンスを作成できます。
問題C.テーブルパーティション
この問題では、ゼロと1のテーブルのパーティションの数を9つの部分に計算する必要があり、これらの部分の指定された5つの部分のユニット数は偶数になりました。

この問題を解決する方法はいくつかありますが、そのうちの1つを検討します。 c1、c2、r1、およびr2を修正します。 r2が1パリティ分増加した場合、ラインr2に偶数個のユニットが含まれていて、それ以外の場合に変化しても、パーツA5、A7、およびA9のユニット数は変化しないことに注意してください。 したがって、固定されたc1、c2、およびr1の場合、適切なr2がわかりやすい-目的の部分のユニット数の偶数に応じて、r2 = n-1の場合、r2 + 1からnで始まる行のユニット数が偶数になるようにr2奇数。 O(n 3 )の解が得られますが、これは割り当てられた制限時間を満たすのに十分ではありません。 ただし、同様の引数をc1およびc2に適用できるようになりました。 固定r1、r2、c1の場合、c2が1増加すると、列c2のユニット数のパリティだけパリティが変更されます。 したがって、r1を固定し、r2 = n-1に設定し、c1を固定すると、大きな行の偶数和または奇数和のr2が適しているc2の値の数を簡単に見つけることができます。
この解の漸近的な振る舞いはすでにO(n 2 )であり、これは与えられた制約の下で十分です。
タスクD.アーカイバ
このタスクには、動的プログラミングまたは貪欲アルゴリズムの少なくとも2つの異なるアプローチが可能です。
シーケンスをツリー形式でアーカイブするプロセスを想像してください。各中間シーケンスの各シンボルはツリーの最上部になり、頂点の子は、アーカイブ中に指定されたものに「接着」される2つの文字になります。 初期数は葉に書き込まれ、タスクはすべての中間の頂点に数を書き込むことですが、アーカイブのペナルティは、異なる数が子に書き込まれる頂点の数に等しくなります。
動的計画法を使用したソリューションは次のとおりです。各頂点uで、この頂点に数値xを書き込む場合、サブツリーの最小合計ペナルティp [u] [x]を格納します。 頂点では、サブツリー内のリーフの1つで発生する数のみを書き留めることが意味があるため、考慮すべきオプションの総数はO(n log n)であることに注意してください。
再計算は次のように実行されます。子vとwを持つ頂点uを考えます。 xの値を書き込む予定があるとします。 p [v] [x]とp [w] [x]の両方が定義されている場合、xをuに入れるオプションの1つはxを両方の子に入れることです。このオプションの価格はp [v] [x] + p [w ] [x]。 xを1つの子だけに入れるオプションもあります。 vにxを配置する場合、このオプションのコストはp [v] [x] + minp [w] + 1で、minp [w]はすべてのyに対するp [w] [y]の最小値です。
DPを使用した解法に代わる方法は、貪欲な解決策です。頂点ごとに、すべての可能な値のリストを保持し、そのうちの1つを最上部に置いて、サブツリーで最小ペナルティを取得します。 頂点の最適なセットを見つけるには、その子に最適な値のみを入れようとするだけで十分であることがわかります。 さらに、子の最適値のリストが交差する場合は、これらの数値のいずれかを取る必要があります。 それらが交差しない場合、各子の意味のいずれかが実行されます。
演習として、提示されたアルゴリズムの正確性の証明を残します。
問題E.ブラックジョン
この問題では、合計が1になるように分数(カード)のサブセットを選択する必要があります。 したがって、この問題はバックパック問題の特殊なケースです。 問題を解決するための可能なアプローチの1つは、すべての分数を共通の分母にすることです。 ただし、可能なすべての分母の最小公倍数(LCL)は232,792,560であり、結果の「クラシック」バックパックの問題をさらに解決するには数値が大きすぎます。
この問題を解決するには、独立したサブタスクに分解する必要があります。 これを行うには、分母に応じて5つのグループに分数を分割します:分母11、13、17、19、および他のすべての分数を持つ分数。 合計内のこれらのグループのいずれかから選択された分数が整数にならない場合、他のグループから整数への分数で補うことができないことに注意してください。 この事実は、大きな単純な分母が別のグループに割り当てられ、それ以外の分母がそれ自体の倍数になることはできないという事実によるものです。
各グループで、選択された分数の合計は整数である必要があり、ゼロである可能性もあります。 各グループのバックパック問題を解いて、特定の整数を取得するためにグループ内の分数を選択できるかどうかを調べます。 -100から100までの整数のみが対象です。これは、モジュロがそれぞれ1を超えない100個以下の端数の合計、モジュロが100を超えないためです。また、最後のグループのすべての可能な分母のLCは5040のみであることに注意してください。分子の可能なオプションの数は合計で1 008 001を超えません。この事実により、割り当てられた時間内に各グループのバックパックの問題を解決できます。
各グループでどの整数を取得できるかを知っているため、各グループで1つの整数を選択することで、1に等しい量を取得できるかどうかを確認する必要があります。 この問題は、動的計画法を使用して解決できます。 量a i 、 jを導入します-最初のiグループの分数を使用して、正確にjの合計を取得することは可能ですか? ベースは、ゼロを除く-100から100までのjの値a 0、0 = trueおよびa 0 、 j = falseになります。 遷移は次のように実行されます:a i 、 j =少なくとも1つのkがtrue(a i-1 、 jkおよびb i、k )の場合はtrue、そうでない場合はfalse、ここでb i、kはグループiは、和kの分数を選択します。 問題に対する答えは5.1の値になります。
取得する必要がある分数のセットを見つけるには、見つかったダイナミクス値を使用するだけで十分であり、各グループに対して、バックパック問題の答えを復元する標準的な方法を使用します。
タスクF.ケーキを切る
それに沿ったカットがケーキを2つの部分に分割し、そのうちの1つに桜が1つなく、少なくとも1つのバラがある場合、直線を良いと呼びます。 さらに、線が軸Oxと形成する角度を興味深いと呼びます。 良い線の最小の興味深い角度を見つけることが必要です。
最小の興味深い角度で良い線を考えてください。 そのような線が存在するのは、問題の状態によって、バラやサクランボを通る線を通過するときに、それらが属するピースを選択できるためです。 そうしないと、極値点であるラインが存在しません。 次のとおりです。この線は水平であるか、桜とバラを通過します。 確かに、良い直線が水平ではなく、桜やバラを通過しない場合は、興味深い角度を減らす方向にわずかに回転させて、良好なままにすることができます。 後者は、興味深い角度の最小条件と矛盾します。
水平方向の良好な線があるかどうかを確認するのは簡単です。 これを行うには、最大縦座標のチェリーを通る水平線を確認します。 答えの残りの候補は、fromからさくらんぼの凸包への接線です。
回答の候補であるすべての行を直接確認できます。 最も難しいのは、与えられたポイントから凸包への接線を構築することです。 これを行うには、凸包のすべての頂点をソートします。 そのようなソリューションの漸近的動作の合計はO(mn)になり、このアプローチを実装するプログラムは時間制限に適合しません。
接線を見つけるためのより効率的な方法を考え出すことができます。 別の観察を使用することをお勧めします。 与えられた点から凸型の図形への興味深い接線角がβであると仮定します。 β≤α≤π/ 2とします。 次に、興味深い角度αを持つこの図形の接線の1つが、この図形とポイントを分離します。
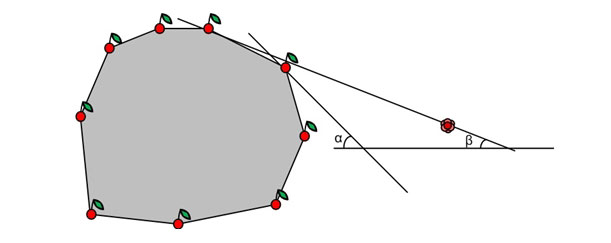
最後の観測を使用して、興味深い角度がαを超えない良好な線が存在するかどうかを確認できます。 これを行うために、興味深い角度αを持つチェリーの凸包のすべての接線を描画します。 その後、接線の1つとチェリーが反対側にあるように、少なくとも1つのバラがあることを確認します。 これは線形時間で簡単に実行できます。

少なくとも1本のバラが暗い領域にない場合、答えはα以下です。 逆もまた真です。
その後、希望する角度をバイナリ検索で見つけることができます。
その結果、漸近O(N(log N + I))で解を取得します。ここで、N = n + mであり、Iはバイナリ検索の反復回数です。
ロシアコードカップ2012でお会いしましょう!
チームロシアコードカップ。