
分析とは何ですか?
アルゴリズムを分析することにより、このアルゴリズムを使用してこの問題を解決するのにかかる時間を知ることができます。 同じ問題は、さまざまなアルゴリズムを使用して解決できます。 アルゴリズム分析は、アルゴリズムを選択するためのツールを提供します。
アルゴリズムの分析結果は、特定のアルゴリズムが必要とする正確な秒数またはコンピューターサイクルの公式ではありません。 N + 5操作を行うアルゴリズムとN + 250操作を行うアルゴリズムの違いは、Nが非常に大きくなるとすぐに見えなくなることを理解する必要があります。
入力クラス
アルゴリズムを分析するとき、入力データの選択はその実行に大きく影響する可能性があります。 入力リストが既に並べ替えられている場合、いくつかの並べ替えアルゴリズムは非常に迅速に機能しますが、他のアルゴリズムはそのようなリストに対して非常に控えめな結果を表示します。 しかし、ランダムなリストでは、結果が反対になる場合があります。 したがって、単一の入力データセットでアルゴリズムの動作を分析することに限定するつもりはありません。 実際には、アルゴリズムの実行速度が最も速いデータと最も遅いデータの両方を探す必要があります。 さらに、考えられるすべてのデータセットでアルゴリズムの平均効率を評価することは有用です。
ベストケース
最良の場合のアルゴリズムの実行時間は、多くの場合非常に短いか、単に一定であるため、このような分析はほとんど実行されません。
最悪の場合
最悪の場合の分析は、アルゴリズムの最大実行時間を想像できるため、非常に重要です。 最悪のケースを分析するときは、アルゴリズムが最も機能する入力を見つける必要があります。
ミディアムケース
多くの異なる詳細を考慮する必要があるため、平均的なケースの分析は最も困難です。 分析は、可能な入力データセットを分割する必要があるさまざまなグループの定義に基づいています。 2番目のステップでは、入力データセットが各グループに属する確率が決定されます。 3番目のステップでは、各グループのデータに対するアルゴリズムの実行時間が計算されます。 1つのグループのすべての入力データに対するアルゴリズムの実行時間は同じである必要があります。そうでない場合は、グループをさらに分割する必要があります。 平均ランタイムは、式によって計算されます

ここで、nは入力データのサイズを示し、mはグループの数を示します。 piを介して、入力データが番号iのグループに属する確率、およびtiを介して、アルゴリズムが番号iのグループからのデータを処理するのに必要な時間。
ほとんどの場合、各グループに分類される入力データの確率は同じであると仮定します。 言い換えると、5つのグループがある場合、最初のグループに入る確率は2番目のグループに入る確率と同じです。つまり、確率
各グループに入るのは0.2です。 この場合、平均稼働時間は、前の式を使用して推定するか、同等の式を使用することができます

下限。 決定木。
この問題を解決する他のアルゴリズムがこれより速く動作しない場合、アルゴリズムは最適です。 アルゴリズムの最適性を見つける方法は? これを行うには、問題を解決するために必要な操作の最小数(下限と呼ばれる)を知る必要があります。 ただし、このためには、特定のアルゴリズムではなく、TASKを調べる必要があります!
例として、バイナリツリーを使用して3つの数値のリストをソートするプロセスの分析を検討します。 このようなツリーは、決定ツリーと呼ばれます。

このツリーの最長パスは最悪の場合に対応し、逆もまた同様です。最短のパスが最短になります。 平均的なケースは、ツリーのエッジの数をシートの数で割った商として説明されます。
2つの要素の再配置のために、組み合わせ論の規則に従って、N個の要素に対して1枚のシートがあります! シート。 レベルKのシート数は2k-1です。したがって、決定ツリーにはLレベルがあります。ここで、LはN! ≤2L-1 対数、我々は得る
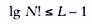
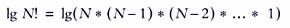

最終的に、次のようになります。
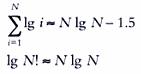
そのため、順序O(NlgN)のソートアルゴリズムが最適であり、最適と見なすことができることを学びました。 さらに、この調査から、O(NlgN)操作よりも速くソート問題を解決するアルゴリズムが正しく機能しないことがわかります!