数値システムの基礎

エンコーディングを勉強すると、数字の体系を十分に理解していないことに気付きました。 それにもかかわらず、彼はしばしば2、8、10、16番目のシステムを使用し、相互に転送しましたが、すべては「マシン」で行われました。 多くの出版物を読んだ後、私はそのような基本的な資料に関する単一の、簡単な言語の記事の欠如に驚きました。 それが私が自分で書くことに決めた理由です。そこで私は、アクセス可能で整然とした方法で数体系の基本を説明しようとしました。

はじめに

番号体系は、 番号を記録（表現）する方法です。



これはどういう意味ですか？ たとえば、目の前にいくつかの木があります。 あなたの仕事はそれらを数えることです。 これを行うには、次のことができます-指を曲げる、石に刻み目を入れる（1本の木-1本の指/ノッチ）、または10個のオブジェクトをいくつかの木（石など）に割り当て、1つのコピー-スティックを数えて、それらを地面に置きます。 最初のケースでは、番号は曲がった指またはニックの文字列として表され、2番目では-左が石、右が棒である石と棒の組み合わせ



番号体系は、定位置と非定位置に分けられ、位置は順番に同種と混合に分けられます。



非定位置 -最も古い番号で、数字の各桁はその位置（ランク）に依存しない値を持ちます。 つまり、ダッシュが5つある場合、各ダッシュは行内の位置に関係なく、1つの単一アイテムのみに対応するため、数字も5になります。



位置システム -各桁の値は、番号内の位置（ランク）に依存します。 たとえば、私たちにとって馴染みのある10番目の数値システムは定位置です。 数値453を検討してください。数値4は数百の数を表し、数値400に対応します。5-数10であり、値50に似ています。3-単位と値3です。 最終的な数は、400 + 50 + 3 = 453の合計として表すことができます。



同種システム -数値のすべての数字（位置）について、有効な文字（数字）のセットは同じです。 例として、前述の10番目のシステムを取り上げます。 同種の10番目のシステムで数値を記述する場合、各桁で使用できるのは0〜9の1桁のみであるため、数値450が許可されます（1桁目-0、2桁目-5、3桁目-4）。 4F5はそうではありません。これは、文字Fが0から9までの数字のセットに含まれていないためです。



混合システム -数字の各桁（位置）で、有効な文字（数字）のセットが他の数字のセットと異なる場合があります。 鮮やかな例は、時間測定システムです。 秒と分のカテゴリでは、60の異なる文字（「00」から「59」）、時間のカテゴリでは-24の異なる文字（「00」から「23」）、曜日のカテゴリでは-365などが可能です。

非位置決めシステム

人々が数えることを学ぶとすぐに、数字を書く必要がありました。 初めは、すべてが単純でした-表面上のノッチまたはダッシュは、1つのオブジェクト、たとえば1つの果物に対応していました。 それで最初の数字システムが登場しました-シングル。

シングルナンバーシステム

この番号体系の番号はダッシュ（スティック）の文字列で、その番号はこの番号の値に等しくなります。 したがって、100個の日付のクロップは、100個のダッシュで構成される数に等しくなります。

しかし、このシステムには明らかな不都合があります-数字が大きいほど、スティックの列が長くなります。 さらに、誤って余分なスティックを追加したり、逆に追加しないことで、数字を書くときに間違いを犯しやすくなります。



便宜上、人々はスティックを3、5、10個にグループ化し始めました。 同時に、各グループは特定の記号またはオブジェクトに対応していました。 最初は、指がカウントに使用されたため、最初の兆候は5個と10個のグループ（ユニット）に現れました。 これにより、より便利な番号記録システムを作成することができました。

古代エジプトの十進法

古代エジプトでは、数字1、10、10 2、10 3、10 4、10 5、10 6、10 7を示すために特殊文字（数字）が使用されていました。 それらのいくつかを次に示します。







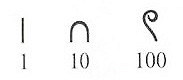
なぜ小数と呼ばれますか？ 前述のように、人々はシンボルをグループ化し始めました。 エジプトでは、10のグループを選択し、数字の「1」は変更しません。 この場合、数値10は10進数システムの基数と呼ばれ、各文字は数値10をある程度表現したものです。



古代エジプトの数字体系の数字は、これらの組み合わせとして書かれていました

各文字は9回まで繰り返されます。 合計値は、数値の要素の合計に等しくなりました。 値を取得するこの方法は、各非位置番号システムの特性であることは注目に値します。 例は番号345です：

バビロニアの6進法

エジプトとは対照的に、バビロニアのシステムでは、2つのシンボルのみが使用されました。ユニットを示す「まっすぐな」ウェッジと、数十の「横たわる」ウェッジです。 数値の値を決定するには、数値の画像を右から左に数字に分割する必要があります。 新しい退院は、横umb位の後に直接くさびが現れることから始まります。 例として32を取り上げます。



数字の60とそのすべての角度は、「1」として直線のくさびでも示されます。 したがって、バビロニアの数体系は6進数と呼ばれていました。

1から59までのすべての数字は、10進数の非定位システムでバビロニア人によって書かれ、大きな値-60を基数とする定位置で書かれました。



ゼロを表す数字がなかったため、番号の記録はあいまいでした。 数値92の表現は、92 = 60 + 32だけでなく、たとえば3632 = 3600 + 32も意味します。 数字の絶対値を決定するために、欠落している6桁の数字を示す特殊文字が導入されました。これは、10進数レコードの数字0の出現に対応します。



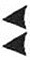
これで、番号3632は次のように記述されます。







6桁の10進数のバビロニアシステムは、位置の原理に部分的に基づいた最初の数値システムです。 この数値システムは、たとえば、時刻を決定するときに使用されます。1時間は60分で構成され、1分は60秒です。

ローマ系

ローマのシステムはエジプトのシステムと大差ありません。 その中で、数字1、5、10、50、100、500、および1000を示すために、ラテンアルファベットの大文字は、それぞれI、V、X、L、C、D、およびMです。 ローマ数字システムの数字は、連続した数字のセットです。



数値の値を決定する方法：

1. 数値の値は、その数字の値の合計に等しくなります。 たとえば、ローマ数字システムの数値32は、XXXII =（X + X + X）+（I + I）= 30 + 2 = 32という形式です。
2. 小さい数字が大きい数字の左側にある場合、値は大きい数字と小さい数字の差に等しくなります。 同時に、左の桁は右の桁より1桁小さいことがあります。したがって、「若い」だけのL（50）とC（100）の前にX（10）が立つことができ、D（500）とM（1000）の前にのみ- C（100）、V（5）の前-I（1）のみ。 考慮される番号体系の番号444は、CDXLIV =（DC）+（LX）+（VI）= 400 + 40 + 4 = 444の形式で記述されます。
3. 値は、1ポイントと2ポイントに収まらないグループと数値の値の合計に等しくなります。

デジタルに加えて、アルファベット（数字）の数値システムもあります。その一部を次に示します。

1）スラブ

2）ギリシャ語（イオニア語）

位置番号システム

上記のように、位置システムの出現のための最初の前提条件は古代バビロンで生じました。 インドでは、システムはゼロを使用した位置10進数の形式をとり、インド人はこのシステムをアラブ人から借用し、そこからヨーロッパ人が採用しました。 何らかの理由で、ヨーロッパでは、このシステムに「アラブ」という名前が割り当てられました。

10進数システム

これは最も一般的な番号システムの1つです。 商品の価格を呼び出し、バスの番号を発音するときに使用します。 各カテゴリ（位置）では、0〜9の範囲で1桁しか使用できません。システムの基数は10です。



たとえば、数値503を取得します。この数値が非定位システムで記述された場合、その値は5 + 0 + 3 = 8でした。しかし、位置システムがあるため、数値の各桁にシステムの底、この場合は数値「 10”、放電数に等しい電力に上げられます。 値は5 * 10 ² + 0 * 10 ¹ + 3 * 10 ⁰ = 500 + 0 + 3 = 503であることがわかります。複数の数値システムを同時に操作する際の混乱を避けるため、ベースは下付き文字で示されています。 したがって、503 = 503 ₁₀です。



10進数システムに加えて、2番目、8番目、および16番目のシステムには特別な注意が必要です。

2進数システム

このシステムは、主にコンピューター技術で使用されます。 なじみのある10番目のものを使用しなかったのはなぜですか？ 最初のコンピューティングマシンはBlaise Pascalによって作成されましたが、10進法を使用していましたが、10州で動作可能なデバイスの生産が必要になり、価格とマシンの合計サイズが増加したため、現代の電子マシンでは不便でした。 これらの欠点は、2番目のシステムで機能する要素を奪われています。 それでも、問題のシステムはコンピューターの発明よりもずっと前に作成され、インカ文明にさかのぼります。インカ文明では、複雑なロープの束と結び目が使用されていました。



2進数の位置番号システムの基数は2であり、2文字（数字）を使用して数字2を書き込みます：0および1。各数字では、1桁のみ（0または1）が許可されます。



例は101です。これは、10進数システムの番号5に似ています。 2番目から10番目に転送するには、2進数の各桁にベース「2」を掛けて、カテゴリに等しい累乗にする必要があります。 したがって、数値101 ₂ = 1 * 2 ² + 0 * 2 ¹ + 1 * 2 ⁰ = 4 + 0 + 1 = 5 ₁₀ 。



マシンでは、2番目の数値システムの方が便利ですが、よく見られるように、コンピューターの10番目のシステムで数値を使用します。 次に、ユーザーが入力した数字をマシンがどのように判断しますか？ 0と1の2文字しか使用できないため、あるシステムから別のシステムに数字はどのように変換されますか？



コンピューターが2進数（コード）を処理するには、それらをどこかに保存する必要があります。 個々の数字を格納するために、電子回路であるトリガーが使用されます。 2つの状態があり、1つはゼロに対応し、もう1つは統一に対応します。 単一の数値を記憶するために、レジスターが使用されます。トリガーのグループは、2進数のビット数に対応します。 そして、レジスタのセットはRAMです。 レジスタに含まれる番号は機械語です。 ワードを使用した算術および論理演算は、算術論理デバイス（ALU）によって実行されます。 レジスタへのアクセスを簡単にするために、番号が付けられています。 この番号はレジスタアドレスと呼ばれます。 たとえば、2つの数字を追加する必要がある場合は、数字自体ではなく、それらが配置されているセル（レジスタ）の番号を示すだけで十分です。 アドレスは8進および16進システムで記述されます（以下で説明します）。アドレスからバイナリシステムへの移行およびその逆の移行は非常に簡単だからです。 2番目から8番目に転送するには、3桁のグループに右から左に分割し、16から4に移動する必要があります。左端のグループに数字がない場合は、左側にゼロが埋め込まれます。リード。 例として、番号101100 _{2を使用し}ます。 8進数では101 100 = 54 ₈であり、16進数では0010 1100 =216です。 すばらしいですが、なぜ画面に10進数と文字が表示されるのですか？ キーが押されると、電気インパルスの特定のシーケンスがコンピューターに送信され、各シンボルには独自の電気インパルスのシーケンス（ゼロと1）があります。 キーボードおよびスクリーンドライバープログラムは、文字コードテーブル（たとえば、65536文字をエンコードできるUnicode）にアクセスし、受信したコードがどの文字に対応するかを判断し、画面に表示します。 したがって、テキストと数字はコンピューターのメモリのバイナリメモリに保存され、プログラムで画面上の画像に変換されます。

8進数システム

バイナリのような8番目の数値システムは、デジタルテクノロジーでよく使用されます。 基数は8で、0〜7の数字を使用して番号を記録します。



8進数の例：254。10番目のシステムに転送するには、元の数値の各ビットに8 ^nを乗算する必要があります（nはビットの数）。 254 ₈ = 2 * 8 ² + 5 * 8 ¹ + 4 * 8 ⁰ = 128 + 40 + 4 = 172 ₁₀です。

16進表記

16進数システムは、現代のコンピューターで広く使用されています。たとえば、＃FFFFFF-白い色が使用されています。 問題のシステムの基数は16で、数字の書き込みに使用します：0、1、2、3、4、5、6、7、8、9、A、B。C、D、E、F。文字は10、11です。それぞれ12、13、14、15。



例として4F5 ₁₆を取り上げます。 8進数に変換するには、最初に16進数を2進数に変換してから、3桁のグループに分けて8進数に変換します。 数値を2番目に変換するには、各桁を4ビットの2進数として表す必要があります。 4F5 ₁₆ =（100 1111 101） ₂ 。 しかし、グループ1と3には放電がないので、先頭に0100 1111 0101をそれぞれ埋めます。次に、結果の数値を右から左へ3桁のグループに分割する必要があります。01001111 0101 = 010 011 110101。各バイナリグループを8進システムに変換します。各桁に2 ^nを乗算します。ここで、nは桁番号です：（0 * 2 ² + 1 * 2 ¹ + 0 * 2 ⁰ ）（0 * 2 ² + 1 * 2 ¹ + 1 * 2 ⁰ ）（1 * 2 ² + 1 * 2 ¹ + 0 * 2 ⁰ ）（1 * 2 ² + 0 * 2 ¹ + 1 * 2 ⁰ ）= 2365 ₈ 。



検討中の位置番号システムに加えて、他にも次のようなものがあります。

1）三位一体

2）第四紀

3）十二指腸



位置システムは同種と混合に分けられます。

同種の位置番号システム

記事の冒頭に示した定義は同種のシステムを適切に説明しているため、改良は不要です。

混合数システム

上記の定義に定理を追加できます。「P = Q ⁿ （P、Q、nが正の整数で、PとQが底）の場合、混合（PQ）数体系の任意の数の表記は基数Qの番号体系に同じ番号を書くことにより。」



定理に基づいて、PthシステムからQthシステムへ、およびその逆の転送のルールを定式化できます。

1. QthからPthに転送するには、Qthシステムで数値を必要とし、右桁で始まるn桁のグループに分割し、Pthシステムで各グループを1桁に置き換えます。
2. PthからQthに転送するには、Pthシステムの数値の各桁をQthに変換し、左の桁を除いて欠落している桁を先行ゼロで埋める必要があります。これにより、ベースQのシステムの各数値はn桁で構成されます。

顕著な例は、バイナリから8進数への変換です。 ₂進数10011110 _2を取得して8進数に変換し、右から左に3桁のグループに分割します：010 011 110、各桁に2 ^nを掛けます。ここでnは桁番号、010 011 110 =（0 * 2 ² +1 * 2 ¹ + 0 * 2 ⁰ ）（0 * 2 ² + 1 * 2 ¹ + 1 * 2 ⁰ ）（1 * 2 ² + 1 * 2 ¹ + 0 * 2 ⁰ ）= 236 ₈ 。 10011110 ₂ = 236 _8であることがわかります。 明確にするために、2進数の8進数の画像は、236 ₈ =（10 011 110） _2-8のトリプルに分割されます。



混合番号システムも、たとえば次のとおりです。

1）階乗

2）フィボナッチ

ある番号システムから別の番号システムへの転送

ある番号システムから別の番号システムに番号を変換する必要がある場合があるため、異なるシステム間の転送方法を検討します。

10進数に変換

基数bの数体系には数a ₁ a ₂ a ₃があります。 10番目のシステムに転送するには、数値の各ビットにb ⁿを乗算する必要があります。ここで、nはビットの数値です。 したがって、（a ₁ a ₂ a ₃ ） _b =（a ₁ * b ² + a ₂ * b ¹ + a ₃ * b ⁰ ） ₁₀ 。



例：101 ₂ = 1 * 2 ² + 0 * 2 ¹ + 1 * 2 ⁰ = 4 + 0 + 1 = 5 ₁₀

小数から他への変換

全体：

1. 10進数の整数部を、10進数がゼロになるまで変換するシステムのベースで順次分割します。
2. 除算によって得られる残基は、目的の数の数字です。 新しいシステムの番号は、最後の残りから開始して書き込まれます。

小数部：

1. 10進数の小数部には、変換先のシステムの基数が乗算されます。 部品全体を分離します。 0に等しくなるまで、小数部に新しいシステムの底を掛け続けます。
2. 新しいシステムの数字は、受信に対応する順序での乗算結果の部分です。

例：15 ₁₀を8進数に変換します。

15 \ 8 = 1、剰余7

1 \ 8 = 0、剰余1



下から上にすべての残差を書き留めると、最終的な数値17が得られます。したがって、15 ₁₀ = 17 ₈です。

2進数から8進数および16進数への変換

8進数に変換するには、2進数を右から左に3桁のグループに分割し、欠落している極端な桁を先行ゼロで埋めます。 次に、数字に2 ^nを順番に掛けて各グループを変換します。ここで、nは数字です。



例として、番号1001 _{2を使用し}ます：1001 ₂ = 001 001 =（0 * 2 ² + 0 * 2 ¹ + 1 * 2 ⁰ ）（0 * 2 ² + 0 * 2 ¹ + 1 * 2 ⁰ ）=（0+ 0 + 1）（0 + 0 + 1）= 11 ₈



16進数に変換するには、2進数を右から左に4桁のグループに分割し、2番目から8番目への変換と同様に行います。

8進数および16進数から2進数に変換する

8進数から2進数への変換-8進数の各桁を2で除算して2進数の3桁の数値に変換します（除算の詳細については、上記の「10進数システムから他のシステムへの変換」セクションを参照）、欠落している極端な桁を先行ゼロで埋めます。



たとえば、数字45 _8を考えてみましょう：45 =（100）（101）= 100 101 ₂



16番目から2番目への変換-16進数の各桁を2で割って4桁の2進数に変換し、欠落している極端な桁を先行ゼロで埋めます。



任意の数値システムの小数部分を10進数に変換します



変換は、全体の場合と同じ方法で実行されますが、数字の桁に「-n」の累乗が乗算されます。nは1から始まります。



例：101.011 ₂ =（1 * 2 ² + 0 * 2 ¹ + 1 * 2 ⁰ ）、（0 * 2 ^-1 + 1 * 2 ^-2 + 1 * 2 ^-3 ）=（5）、（0 + 0 、25 + 0.125）= 5.375 ₁₀

バイナリシステムの小数部分を8番目と16番目に変換する

小数部分は、数字の整数部分と同じ方法で変換されます。ただし、3桁と4桁のグループへの分類は小数点の右側になり、欠落している桁は右側にゼロが追加されます。



例：1001.01 ₂ = 001 001、010 =（0 * 2 ² + 0 * 2 ¹ + 1 * 2 ⁰ ）（0 * 2 ² + 0 * 2 ¹ + 1 * 2 ⁰ ）、（0 * 2 ² + 1 * 2 ¹ + 0 * 2 ⁰ ）=（0 + 0 + 1）（0 + 0 + 1）、（0 + 2 + 0）= 11.2 ₈

10進数システムの小数部を他のシステムに変換します

数値の小数部分を他の数値システムに変換するには、整数部分をゼロに変換し、結果の数値に変換先のシステムの基数を掛け始める必要があります。 乗算の結果、整数部分が再び表示される場合、結果の整数部分の値を以前に記憶（書き留め）して、ゼロに戻す必要があります。 小数部分が完全に消えると、操作は終了します。



たとえば、10.625 ₁₀をバイナリシステムに変換します。

0.625 * 2 = 1.25

0.250 * 2 = 0.5

0.5 * 2 = 1.0

上から下にすべての残高を書いた後、10.625 ₁₀ =（1010）、（101）= 1010.101 ₂を取得します