確かに、あなたはすでにこのような「啓示」をインターネット上で、主にツイッター上で何度も見ました。 年に2、3回、洪水は必然的に珍しい出来事である1か月の金曜日、土曜日、日曜日に5回発生します。
この喜びの理由は完全に理解できます-なぜなら、今月は通常の休日や酔っ払う日が多いからです! ただ、1年のうちのそのような日がもはや遅れないという認識が遅れているということです。
しかし、私は洪水と無慈悲な喜びに激怒しているのではなく、これが823年に1回起こるようなまれな出来事であるとの陳述の愚かさにbyしています。 誰もがこの声明の正確さを考えずに、オウムのように次々にこれを繰り返します。 一方、これは最も率直なナンセンスです。なぜなら、そのような月は、カレンダーの気の弱い「専門家」が言うよりもはるかに頻繁に落ちるからです。
そのような出来事が最後に起こったとき、私は怒りと怒りを一人の善良な人に向けました。 しかし、今後はこの間違いを繰り返さず、短い記事である教育プログラムを作成し、オウムをすべて送ることにしました。
奇跡の座標
まず、金曜日、土曜日、日曜日の5つの特別な月が何であるかを考えてみましょう。 たとえば、同じ2011年7月を取り上げます。
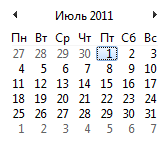
ご覧のとおり、1か月で5つの金曜日、土曜日、日曜日(このような月を「魔法」と呼びます)は、次の2つの条件が満たされた場合にのみ可能です。
- 月は31日間で構成される必要があります。
- 月は金曜日に開始する必要があります。
カレンダーには、31日間の7か月(1月、3月、5月、7月、8月、10月、12月)があります。 金曜日から始まる月も珍しくありません。 たとえば、2010年10月、2010年1月などです。
より深く掘る
さらに、この月またはその月が始まる日は、年が始まる曜日と、今年がle年であるかどうか(1月を除くすべての月)にのみ依存します。 「年/うるう年-月」のペアごとに、曜日の違いの変化は一定です。 表をご覧ください。
実際、このシフトは毎月累積され、各月の7日目で割った余りに等しくなります(1月-3、2月-0または1、3月-3など)。 つまり、シフトは各月の31日間は3日間、30日間の月は2日間、2月は0/1日になります。これは特別な年(うるう年は1日間)です。
オフセットは、7による除算の剰余として表示されることに注意してください(つまり、 7を法とする剰余類の輪があります )。
テーブル番号1。
| 月 | 毎月
変位 | 毎月
変位(ぶら下げ) | からのオフセット
年の初め | からのオフセット
年の初め(vis。) |
|---|---|---|---|---|
| 1月 | 3 | 3 | 0 | 0 |
| 2月 | 0 | 1 | 3 | 3 |
| 行進 | 3 | 3 | 3 | 4 |
| 4月 | 2 | 2 | 6 | 0 |
| 5月 | 3 | 3 | 1 | 2 |
| 6月 | 2 | 2 | 4 | 5 |
| 7月 | 3 | 3 | 6 | 0 |
| 8月 | 3 | 3 | 2 | 3 |
| 9月 | 2 | 2 | 5 | 6 |
| 10月 | 3 | 3 | 0 | 1 |
| 11月 | 2 | 2 | 3 | 4 |
| 12月 | 3 | 3 | 5 | 6 |
年の結果によると、合計変位は通常の年で1、うるう年で2になります。これは完全に真実です。365を7で割った余りは1で、366を除算した余りは2です。
真実を光に
そのため、取得したい結果が得られました。金曜日に開始する月が必要です。 私たちは年の初めからの変化を知っているので、今月が「魔法」になるように、各月の年が始まる日を決定するのは簡単です。
次の表は、前の表の続きです(ここでは7か月のみに関心があります)。 つまり、各月について、年が始まる曜日を取得するため、この月は「魔法」になります。
テーブル番号2。
| 月 | 求めた
年の初め | 求めた
年の初め(vis。) |
|---|---|---|
| 1月 | 金曜日 | 金曜日 |
| 行進 | 火曜日 | 月曜日 |
| 5月 | 木曜日 | 火曜日 |
| 7月 | 土曜日 | 金曜日 |
| 8月 | 水曜日 | 火曜日 |
| 10月 | 金曜日 | 木曜日 |
| 12月 | 日曜日 | 土曜日 |
今年は土曜日に始まり、le年ではないため、7月は「魔法のよう」になっています。
そのような月はほぼ毎年であることがわかります:
テーブル番号3。
| 年の初め | 「マジック」ヶ月 | 「マジック」月(vis。) |
|---|---|---|
| 月曜日 | - | 行進 |
| 火曜日 | 行進 | 5月、8月 |
| 水曜日 | 8月 | - |
| 木曜日 | 5月 | 10月 |
| 金曜日 | 1月、10月 | 1月、7月 |
| 土曜日 | 7月 | 12月 |
| 日曜日 | 12月 | - |
「魔法の」月はそれほど珍しくありません。 1年で2か月もあります。 時々、一年中そのような月はないことがあります。
823年ごと
ここで、「魔法の」7月は823年に1回起こるという論文を考えてみましょう。 すでに示したように、このような7月は、うるう年ではなく、土曜日に始まります。 土曜日から始まる1年というのは本当に珍しいことですか? これはよくあることであり、毎年1日(およびうるう年ごとに2日)のシフトがある場合、これは約7年に1回発生するはずです。
2000年から2022年までの年を見てみましょう(これらが正確になぜであるかを理解します)。
表番号4。
| 年 | 開始する | オフセット |
|---|---|---|
| 2000(vis。) | 土曜日 | 2 |
| 2001 | 月曜日 | 1 |
| 2002 | 火曜日 | 1 |
| 2003 | 水曜日 | 1 |
| 2004(ハング) | 木曜日 | 2 |
| 2005年 | 土曜日 | 1 |
| 2006 | 日曜日 | 1 |
| 2007年 | 月曜日 | 1 |
| 2008(ハング) | 火曜日 | 2 |
| 2009 | 木曜日 | 1 |
| 2010 | 金曜日 | 1 |
| 2011 | 土曜日 | 1 |
| 2012(vis。) | 日曜日 | 2 |
| 2013 | 火曜日 | 1 |
| 2014 | 水曜日 | 1 |
| 2015 | 木曜日 | 1 |
| 2016(ハング) | 金曜日 | 2 |
| 2017年 | 日曜日 | 1 |
| 2018年 | 月曜日 | 1 |
| 2019年 | 火曜日 | 1 |
| 2020(vis。) | 水曜日 | 2 |
| 2021 | 金曜日 | 1 |
| 2022 | 土曜日 | 1 |
したがって、2000年、2005年、2011年、2022年の土曜日から始まりますが、2000年はle年なので、私たちには適していません。 それでも、約20年で「魔法の」7月が3回発生します。 これは、カレンダーを見て自分で確認できます。
そのため、すぐに「魔法の」月が何になるかを簡単に「予測」できます。 そして、これが823年ごとに起こるという事実についてナンセンスを書かないでください。 そして、リツイートしないでください!