 こんにちは、Habr! 今日は、貪欲なアルゴリズムについてお話したいと思います。
こんにちは、Habr! 今日は、貪欲なアルゴリズムについてお話したいと思います。
特定の問題を解決する多くの方法があります: 動的プログラミング 、 列挙 。 貪欲なアルゴリズムは、それほど有名ではなく、かなり一般的です。
彼の人生のすべてのプログラマーは、少なくとも一度は貪欲に、おそらくそれについても考えずに書いたと思います。 これは何? 猫へようこそ。
欲は悪ではない
したがって、 貪欲なアルゴリズムは、最終的な解決策が最適になることを期待して、各ステップでローカルに最適な選択を行うアルゴリズムです。
たとえば、グラフで最短経路を見つけるためのダイクストラのアルゴリズムは非常に貪欲です。これは、すべてのステップで、これまでに行ったことのない最小の重みを持つピークを探し、他の頂点の値を更新するためです。 さらに、頂点で見つかった最短経路が最適であることを証明できます。
ちなみに、グラフ内の最短パスも検索するフロイドのアルゴリズムは(すべての頂点間で)、貪欲なアルゴリズムの例ではありません。 フロイドは別の方法を示します-動的計画法。
欲張りアルゴリズムの使用はかなり標準です。 次のタスクの例として考えてください。
タスクをスケジュールする
フリーランスのプログラマー、Vasya Pupkinにn個のタスクを割り当てます。 各タスクには独自の期限とコストがあります(つまり、このタスクを完了しないと、彼は多くのお金を失います)。 Vasyaはとてもクールなので、1日で1つのタスクを実行できます。 時間0からタスクを開始できます。利益を最大化する必要があります。
貪欲な使用の典型的な例:Vasyaは最も「高価なタスク」を行うために利益を上げますが、最も安価なものは実行できません-それから利益は最大化されます。 質問が発生します:タスクを分散する方法? タスクをコストの降順で整理し、次のようにスケジュールを記入します:注文の締め切り前に少なくとも1つの空き場所がスケジュールにある場合、そのような場所の最後に配置します。そうしないと、時間通りに完了できません。その後、空の席の端に置きます。
次のコードが判明します。
//tasks -
Arrays.sort(tasks); //
TreeSet<Integer> time = new TreeSet<Integer>();
for ( int i = 1; i <= n; ++i) {
time.add(i);
}
int ans = 0;
for ( int i = 0; i < n; ++i) {
Integer tmp = time.floor(tasks[i].time);
if (tmp == null ) { // ,
time.remove(time.last());
} else { // ,
time.remove(tmp);
ans += tasks[i].cost;
}
}
いつ貪欲になりますか?
結論:
人生はマトロイドではなく、人生は有限オートマトンです!
ウィキペディアが示唆するように、 マトロイドはペア(X、I)です。ここで、Xはマトロイドのキャリアと呼ばれる有限集合であり、Iは独立集合のファミリーと呼ばれるXのサブセットの集合です。 次の条件を満たしている必要があります。
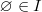
セットIは空ではありません。 元のセットXが空-X =Øだったとしても、1つの要素-空を含むセットで構成されます。 I = {{Ø}}
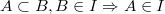
セットIの要素のサブセットも、このセットの要素になります。
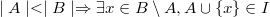
セットAとBがセットIに属し、AのサイズがBより小さいこともわかっている場合、Aに属さないBの要素xがあり、xとAの結合はセットIに属します。このプロパティは完全に自明ではありません。しかし、ほとんどの場合、他のすべての中で最も重要です。
セットXに加法重み関数wが存在する場合、マトロイドは重み付きと呼ばれます。 セットの重みは、その要素の重みの合計として決定されます。
タスク
- 最初のプロパティは明らかに満たされています。 完了したタスクの空のセットがセットに含まれています。 よく、Vasyaがお金をもうけたくないことを気にしないでください。
- 2番目のセットも保持されます。 なぜそうなっているのか:期限の長い順に正常に完了したタスクを並べ替えましょう。 その順序で、それらはまだ正常に実行されます。 この順序で、正常に完了したタスクのサブセットが正常に完了することは明らかです。
- 3番目のプロパティは明らかではありませんが、満たされています。 正常に完了したタスクAとBの2つのセットがあり、| A | <| B |。 デフォルトでは、両方のセットで期限の昇順でタスクをソートします。 AにないBからタスクを取得し、セットAに追加しようとします。Aにスペースがなければ、このタスクが存在しているはずなので、成功します。
なんで? マトロイドの魅力はすべてラド・エドモンズの定理にあります。オブジェクトがマトロイドであることを証明すると、貪欲なアルゴリズムが正しく機能し、正しい結果が生成されます。
貪欲なアルゴリズム自体は次のように実装されます。
 //重量で並べ替え
//重量で並べ替え
 //最初に、答えは空のセットです
//最初に、答えは空のセットです
のために
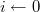 に
に 
もし
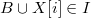 その後//適切な場合
その後//適切な場合
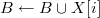 //その後、セットに含める
//その後、セットに含める
参照資料
PS
ところで、スケジュールの問題はO(n)でより速く解決できます。 誰が弱くないですか? (ヒント:TreeSetを別の構造に置き換える必要があります)。