🍾 🚚 🛎️ 手書き数式認識 🏻 💳 ✍🏽

こんにちは、Habr！

この記事では、手書きの数式を認識する経験を共有したいと思います。 Windows7の「Math入力パネル」mip.exeなどの手書き認識ツールは既に存在しますが、この問題を解決するためのさまざまなアプローチが印象的です。 これらのアプローチの1つについてお話します。

小さな紹介

数式の認識は、記号の認識よりも複雑な種類の認識です。数学記号を直接認識することに加えて、数式の構造を認識する必要もあるためです。

手書きの数式のオンライン認識では、通常、次の段階が区別されます。

データ収集と前処理：
式の文字への分離（式のセグメンテーション）：
個々のキャラクターの認識：
数式の構造の認識：

数学的表現の認識の分野での数十年にわたる研究、膨大な数のアルゴリズムと理論が発明されてきました。シンプルなアプローチについてお話しますが、それでも良い結果が得られます。彼は、ステージ1、2、および3が連携して動作し、出力はステージ4で数式として認識される文字のリストであると想定しています。

データ収集と前処理

最初のステップは、データを収集して前処理することです。特定のキャラクタークラスのトレーニングセットは、多くのキャラクターで構成されています。シンボルは順序付けられたストロークのセットであり、ストロークは順序付けられたペアのセット（x、y）です。最初のペアはペンが接触するポイントに対応し、最後は分離ポイントに対応します。各文字は、特定の順序で特定の数のストロークで描画されます。

データの前処理の目的は、ストロークの生データを、さらに分類するためにシンボルのモデルを作成できる形式に変換することです。モデルを簡素化するには、分類に不要な情報を削除する必要があります。ストロークの初期セットは、特定の厳密に固定された次元のベクトルに変換されます。

コントロールポイントの数のスケーリング、シフト、および変更

各ストロークの各ポイントは、開始ポイントがシンボルの境界ボックスの左上隅になるようにシフトされます。その後、シンボルが正方形の内側に配置されるように、幅と高さの比率を維持しながら、すべてのポイントがスケーリングされます。さらに、各ストロークのポイントのセットは、ポイントが等距離になるように変更されます（線形補間によるアークの長さに沿ったオーバーサンプリング）。ポイントの数は固定され、36 / Nに等しくなります。Nはシンボルのストローク数です（36は1、2、3、4で除算され、4は1つのシンボルの最大ストローク数です）。

結論として、ポイントの座標は72要素の単一ベクトルに収集されます。最初の36要素はxの座標を表し、最後のyは座標を表します。

何を得たの？

そして、同じ次元のベクトルのセットを得ました。各クラスの文字は特定の数のベクトルに対応しています。この情報は、たとえば、ニューラルネットワークのトレーニングや、k最近傍アルゴリズムを使用した文字認識に使用できます。

実際、ほとんど情報を失うことなく、ベクトルの次元を数倍減らすことができます。 このアルゴリズムは「主成分法」と呼ばれます。

その結果、分類器をトレーニングするために次のものが作成されました。

個々の文字のセグメンテーションと認識

分類子は文字を個別に認識します。ただし、ストリーミング入力を認識する必要がある場合、文字を構成するストロークと、入力された文字の総数を事前に知ることはできません。したがって、式の文字の数と位置を決定することにより、分類子の機能を補完する必要があります。この問題の解決法は、ストロークを式のセグメンテーションと呼ばれる文字に最適にグループ化することに相当します。

入力されたストロークが時間順に並んでいると仮定します。つまり、3つのストロークで構成される文字を入力すると、この記号のストロークが順番に入力されます。たとえば、 iの後に続く文字を書き込んだ後、文字iの上にドットを置くことはできません。この仮定を前提として、複数のストロークで構成される文字を判別するには、サイズが1からNまでのストロークのグループを順番に検討する必要があります（この例ではNは4です）。複数のストロークからのシンボルが、特定のしきい値よりも小さいエラーで分類器によって認識される場合、このシンボルが優先されます。この場合、考慮される組み合わせの数はF（N）= O（kN）です。分類結果のいずれもがしきい値を超えていない場合、しきい値が増加してステップが繰り返されるか、認識エラーが発生します。

異なるものとして認識できない記号（マイナス記号や分数など）は、1つの記号（水平線）として指定され、構造解析中に名前が変更されることに注意してください。

ストロークの数ごとに有効なシンボルが定義されている場合、セグメンテーションアルゴリズムを改善できます。そのため、2つのストロークは、1つまたは3つのストロークで構成されるシンボルとして認識できません。

また、このアルゴリズムを実装する場合、起こりうるセグメンテーションエラーを防ぐために、誤った結果を即座に修正したり、最後の文字の入力をキャンセルしたりできるインターフェイスが必要です。

あいまいさの解決

分類器は、マイナス記号と小数記号のどちらを入力したかを知ることができません。これには追加の検証が必要です。そのため、マイナス記号の線から上下に一定の距離では、ストロークは検出されず、記号「分数」は配置されます。これに基づいて、記号「スラッシュ」はそれぞれ記号「マイナス」または「分数」に名前が変更されます。ほとんど同じ方法で-小数点と乗算記号を使用します。

最後に、式の構造の認識に移りましょう:-)

発現構造の認識

文字のスコープと属性

数学演算子の関係は、式内のシンボルの位置と相対的なサイズに応じて決定されます。空間領域「左上」、「上」、「上付き」、「下付き」、「下」、「左下」、および「副式」は、関係を定義するために使用されます。たとえば、水平線（分数演算子）のオペランド（分子と分母）は、水平線に対して「上」と「下」の領域にあることが予想されます。

単純な属性（上限、右側の制限など）に基づいて、上限インデックスのしきい値、下限インデックスのしきい値、およびその他の属性を決定できます。これらは、文字の周囲の領域を区切るために使用される数値属性です。また、単純な属性に基づいて、中心点を決定できます。

中心点は、任意の領域のキャラクターの位置を決定する点です。文字の属性を決定するために、文字は上付き文字、下付き文字、または中央文字として分類されます。

各文字クラスには、異なる属性が定義されています。これは、構造解析のあいまいさを回避するために必要です。

発現ベースライン

ベースラインは、式内の文字の水平配置を表すリストです。各シンボルには、異なる空間関係を満たす他のベースラインへのリンクがあります。

キャラクターの優位性と支配的なベースライン

支配は次のように定義されます：aが領域sにあり、sが領域aにない場合、記号sは記号aを支配します。ただし、両方のキャラクターが互いの領域にある可能性があります。その結果、関数dominates(s,a)

計算は次のように実行されます（前のステップでどのシンボルがどちらを支配するかを判断できなかった場合、後続の各ステップが実行されます）。

文字の幾何学的配置を確認します。
文字クラスを確認してください。たとえば、分数文字が数字を支配します。
相対的な文字サイズの確認

L文字の順序付きリストがある場合、次の再帰手順を実行することにより、リスト内の左端の支配的な文字を決定できます。

getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).

getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).
getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).
getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).
getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).

支配的な表現のベースラインは、キャラクターが参照しないベースラインです。数式の読み取り中、通常、最初の左端の支配的な文字が最初に検索され、すべてのベースライン文字が見つかるまで次の支配的な文字などが検索されます。

式を表すデータ構造は、ベースラインツリーと呼ばれます。式があるとします

この式のベースラインツリーは次のようになります。

主要なベースラインDbは、次の関数を使用して構築されます。

constructDominantBaseline(Db,L): 
      

        
        
        
      

      Db ,  Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db)   Hs = getRightNeighbors(s,L)   L,       s  Hs ,        Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)

constructDominantBaseline(Db,L): Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
constructDominantBaseline(Db,L): Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
constructDominantBaseline(Db,L): Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
constructDominantBaseline(Db,L): Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
constructDominantBaseline(Db,L): Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
constructDominantBaseline(Db,L): Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
constructDominantBaseline(Db,L): Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)

constructDominantBaseline(Db,L): 
      

        
        
        
      

      Db ,  Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db)   Hs = getRightNeighbors(s,L)   L,       s  Hs ,        Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)

ベースラインツリーは、Lの順序付きリストで記述された式の支配的なベースラインを再帰的に見つけることによって作成されます。

ConstructBaselineTree(L): 
      

        
        
        
      

      L ,   Db constructDominantBaseline(Db,L)  Db,  ,         s  Db      ,    ,     ,       L = Db     ,   constructBaselineTree    -,    5

ConstructBaselineTree(L): L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
ConstructBaselineTree(L): L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
ConstructBaselineTree(L): L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
ConstructBaselineTree(L): L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
ConstructBaselineTree(L): L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
ConstructBaselineTree(L): L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
ConstructBaselineTree(L): L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5

ConstructBaselineTree(L): 
      

        
        
        
      

      L ,   Db constructDominantBaseline(Db,L)  Db,  ,         s  Db      ,    ,     ,       L = Db     ,   constructBaselineTree    -,    5

結果のツリーは数式の構造であり、解析された後、式エディターのコードに変換できます。私の場合、これはOpenOfficeエディターです。

すべてのこと

そして、このアルゴリズムから判明したアプリケーションである~~GLaDOS~~は、個々の文字を認識する際に間違いを犯す能力がないわけではありませんが、その場でかなり複雑な数式を認識することができました。これはどのように見えるかです：

また、エラーがない場合もありますが、これらの式（および最初に文字認識エラーを見つけた人-よくやった:-)を認識できます

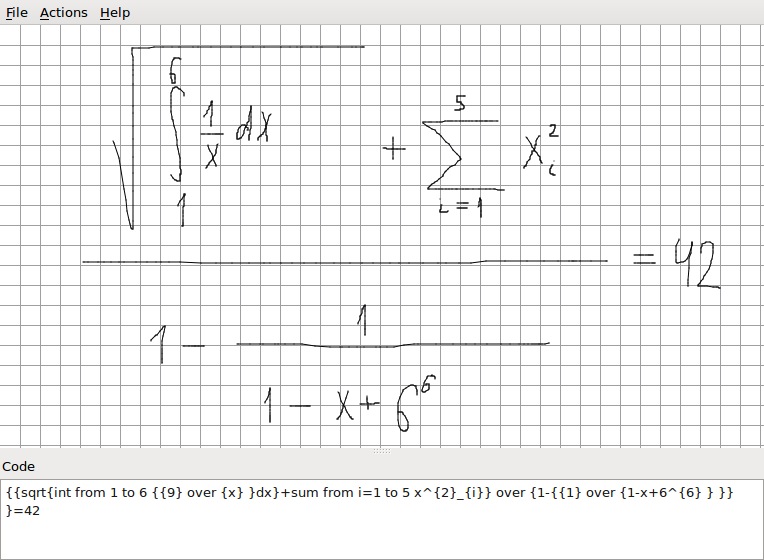
エピローグ

それで、Habréに関する私の最初の記事は終わりました。私は彼女があまり退屈ではなく、誰かに役立つことを願っています！ご清聴ありがとうございました！

参照：

ニコラス・マタキス。手書きの数式の認識。修士論文、マサチューセッツ工科大学、ケンブリッジ、MA、1999年5月。
Ernesto Tapia：数学の理解：オンライン手書き数式の認識システム、ベルリン、2004
Eva Gallardo Perez：CMP数学式オンライン認識システムの2D文法拡張、CMPの研究報告、プラハのチェコ工科大学、No。 3、2009

手書き数式認識