私は最近、より単純なアルファベータフィルターと比較したカルマンフィルターについて言及している拡張現実の投稿を読みました。 長い間、私はFCのコンパイルに関するスニペットのようなものを作っていましたが、今はその時だと思います。 記事では、実際に高度な科学的考察と深い理論的研究に煩わされることなく、拡張FCを実際に構成する方法を説明します。 基本的な概念
- 入出力方程式は微分方程式です（たとえば、第2種ラグランジュ方程式を使用してコンパイルされます）。等号の左側は出力変数に依存する項（システム自身の運動の一般座標）であり、右側は入力変数または空きメンバー。 簡単にするために、次の例を引用することができます：入出力方程式の左側の振り子については、静止位置からの荷重の偏角の項があり、右側には重力やその他の外力の項があります。 そのような方程式がどのように得られるかについては説明しません-無駄な理論計算で出版物を複雑にする必要はありません。 以下では、練習に便利な方法で取得できることを示します。
- 伝達関数（PF）-入力と出力の比率、または入力と出力変数の比率。 比例の規則に従って、
脳を角かっこから外した後、伝達関数は演算子形式で書かれた左側の右側の比率に等しくなります。 - 録音の演算子形式-数式「入出力」は、形式を変更した後、s = d / dtおよびx（t）-> x（s）で記述されます。 その結果、次の形式の方程式：
a1 * x '' + a2 * x '+ a3 * x = b1 * u' + b2 * u、
に変換されます：
（a1 * s ^ 2 + a2 * s + a3）* x（s）=（b1 * s + b2）* u（s）。
この場合、伝達関数は次のようになります。
W（s）= x（s）/ u（s）=（b1 * s + b2）/（a1 * s ^ 2 + a2 * s + a3）
挑戦する
FCのアプリケーションとして、センサーブロックの情報を処理するタスクを取ります（ [1]を参照）。 4ユニットの2軸マイクロメカニカル加速度計（MMA）があります。 8つの測定チャネルのみで、それぞれに対して個別の入出力方程式を作成できます。 ここでは、センサーの製造元の一部（アナログデバイスなど）が近似線形化（この場合は重要）数学モデルを提供していることに注意してください。 卒業証書に取り組んでいるとき、同僚からMatLabのモデルを入手しました。 しかし、たとえ製造業者
したがって、私たち自身が必要なセンサーのモデルを作成できます。 このようにして、1石で2羽の鳥を殺します。単純な線形化モデルを作成し、すでに最低レベルでノイズフィルタリングを導入します。 モデルの単純さについて、センサーのダイナミクスを正確に説明する方程式を使用する場合、次数が大きく異なる数からカルマンフィルター行列を構成する必要があることに注意する必要があります。 前述の加速度計の「メーカーから」モデルでは、最大係数と最小係数の比率は約1e + 10です。 これにより、計算の条件性が極端に低くなります。 係数値の設定における小さな誤差は、非常に大きな計算誤差につながる可能性があります。 数学的モデルに固有の帯域幅を狭めることにより、基本的に計算の安定性が向上します。
それでは、このまさにモデルを作る方法は？ はい、非常に簡単です。 MatLabまたはOctaveパッケージを使用して、必要な帯域幅（ローパスフィルター、ハイパスフィルター、またはバンドパスフィルター）を要求し、パッケージ内のプラグインまたはプラグインを使用して、PFを合成します。 ここで、MatLabパッケージには離散フィルター用の視覚的合成ツールが含まれていることに注意してください。 Octaveでは、まだアナログを見つけていません。 両方のパッケージで、周波数応答曲線と位相応答曲線をプロットできます。これらの曲線では、カットオフの周波数に注意を払う必要があります。また、通過帯域内外の周波数応答グラフの振動にも注意する必要があります。 一般に、周波数応答グラフと位相応答グラフが満たされるまで、伝達関数係数を持つシャーマン。 しかし、私にとっては、もう1つの、より
数学モデル
したがって、簡単にするために、演算子形式の方程式があることに同意します。
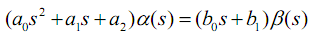
これは、2次の動的リンクの最も一般的な方程式の1つです。 この方程式では、a2-ばね剛性係数の役割を果たします（剛性は、検出要素の位置から静止位置までの距離に直接比例します）。 A1は減衰係数です（動きの速度に比例する力。蜂蜜について覚えておいてください-スプーンを素早く動かすよりもゆっくり動かす方が簡単です）。 a0-慣性を特徴づけます。 等号の右側の係数の意味はわずかに異なります。 これらの係数は、異なる次数のデリバティブでのアクションの有効性を特徴付けます。 ここで、物理的実現可能性の要件により、右側の導関数の最大次数が左側の導関数の最大次数に制限されることを理解することが重要です。
このような方程式を自由に使用できるので、カルマンフィルターの準備の準備を開始できます。 これを行うには、まず入出力方程式を「状態空間」モデルに変換する必要があります。 これは、「コーチー形式」に変換することによって行われます。
まず、プロポーションの形式に変換し、新しい（ダミー）変数を導入する必要があります。
その結果、連立方程式が得られます。
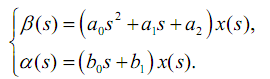
このシステムでは、最初の方程式は動的プロセスの方程式であり、2番目の方程式は観測方程式です。
x1 = xを置き換えることにより、最初の方程式をコーシー形式（1次の微分方程式系）に還元します。
置換の記録の便宜上、このシステムでは逆変換が実行されました。
ラプラス（演算子形式から差分への移行）。 その結果、私たちは破りました
元の方程式を2つの1次方程式に変換します。 導入された変数x1およびx2は、「状態変数」または「位相座標」と呼ばれます。 結果のシステムは、「連続的な」時間で動作します。 元の微分方程式を使用してコンパイルしました。 しかし、コンピューターで位相座標の値を繰り返し計算するための差分アルゴリズム（離散時間のアルゴリズム）を構築する必要があります。 したがって、カルマンフィルターを使用する前に、このシステムを「離散化」する必要があります。 しかし、それについては後で。
次に、入力した位相座標の観測方程式を作成する必要があります。 検討中
置換を導入し、差分形式で取得します。
位相座標インデックスに従って項を配置した後、得られた方程式をベクトル行列形式に書き換える必要があります。
この方程式では
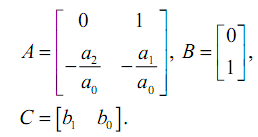
これらの方程式を離散化するには、次の式を使用します。
ここで、Iは単位行列、FとRは状態空間モデルの所望の離散化行列（差分方程式）、tsは量子化周期です。
量子化期間は、サンプリングの重要な要素です。 小さいほど、より正確です
連続時間でモデルの動作を離散モデルで繰り返します。 また、
計算エラーによるtsが大きすぎると、離散モデルは次のようになります
不安定。 被写体があまり動的ではない場合（例：
10 Hzまでの帯域幅）、量子化期間は十分に大きく選択できます。 のために
前述のローパスフィルターでは、0.01秒の大きなマージンで量子化期間を選択できます。
そのため、次の形式の離散モデルを取得しました。
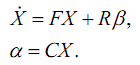
これで、FCモデルを準備する準備がすべて整いました。 各測定チャネルで得られた行列F、R、Cを対角化する必要があります。各測定チャネルに対して、次元2x2の離散固有行列Fがコンパイルされると、独自のカルマンフィルター行列Aが得られます（出版物の冒頭の画像を参照） ）16x16の寸法。 また、列ベクトルR：2x1 * 8チャンネル= 16x8-FCモデルのマトリックスBを使用します。 行ベクトルCから、カルマンフィルターの行列H（8x16）が構成されます。
できた！ 次に、すべてをプログラムする必要があります。 個人的には、このためにRuby + NArrayを使用することを好みます-この束でプロトタイプを作成することは喜びですが、これは私の個人的な意見です...誰に。 これらの方程式を直接プログラミングする価値はないことに注意してください-結果の行列はゼロで非常にまばらです。 考えてみると、すべての行列式はブロック演算に分割できます。 実装段階では、ここで多くの最適化を行う必要があります。
おわりに
表記法について混乱が生じて申し訳ありません。 さまざまな作品からひらめいた式。 投稿の冒頭にある画像のFCの方程式の内容を簡単に説明します。
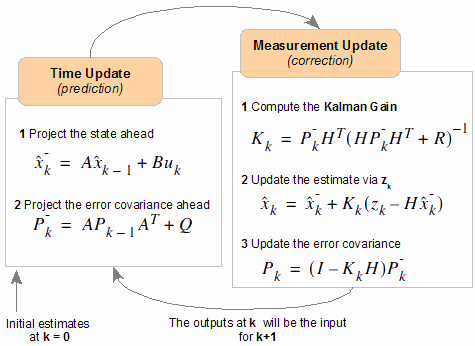
最初に注目するのは、行列P、Q、R、Kです。これは、それぞれ推定誤差（FC問題の解の誤差）の共分散行列、動的プロセスのノイズと測定ノイズの共分散行列、およびカルマンフィルターのゲイン係数の行列です。 ベクトル「x」と「z」は、FCの位相ベクトル（FCモデル内のセンサーブロックの位相ベクトルの模倣）と実際のセンサーの出力信号のベクトルです（実際、これはFCの外部から情報を受信するためのチャネルです）。 提示された図から、FC動作の原理を理解するのは簡単です。
複雑なことは何もないようです。 ただし、FCの作業には多くの重要なニュアンスがあります。 したがって、FCは、いくつかの条件（仮説）で最小二乗平均誤差を与えるアルゴリズムとして設計されています。 まず、ノイズは、ランダム変数のガウス分布を持つ白色（均一なスペクトル応答）です。 しかし実際には、この仮説は満たされていません。 このような理想的なパラメータでノイズの原因を見つけることは困難です。 さらに、測定システム自体の帯域幅は有限です。 この場合、ノイズプロセスの変数もフォトニック結晶の位相ベクトルに含める必要があります。 人工的なアプローチが使用されます。ホワイトノイズのソースがあり、そこから信号がフィルターを通過すると考えられています。 したがって、さらに2つの動的オブジェクトのモデルがFCモデルに追加されます。フィルターは、ホワイトノイズプロセスのペアを動的プロセスのカラーノイズに変換し、ノイズを測定します。
2番目の仮説は、異なる測定チャネルの無相関ノイズです。 また、まれにしか実行されず、この制限を回避するための人為的な方法があります。 これらの方法はすべて、FCの次元の増加につながります。計算の負荷が増加します。
FCの複雑な作業は科学者の
参照資料
- 小型UAV用の非直交SINS
- habrahabr.ru/blogs/augmented_reality/118192
- Brammer K.、Ziffling G. Kalman-Bucyフィルター。 あたり 彼と。 -M。：科学。 ホーム
物理的および数学的な文献の編集。 1982年。 - シジコフV.S. 測定結果を処理する持続可能な方法。 学習ガイド。
-サンクトペテルブルク：「SpetsLit」、1999。-240 p。 - グレッグ・ウェルチ、ゲイリー・ビショップ。 カルマンフィルターの紹介。 TR 95-041、部門
ノースカロライナ大学チャペルヒル校のコンピューターサイエンス。 2004年4月5日。