注釈
この記事は、バイナリイメージの操作に関する記事の最初の部分の続きで書かれており、オブジェクトのカウント方法について説明しています。 ただし、1つのカウントからはほとんど意味がなく、認識されたオブジェクトのいくつかの幾何学的パラメーターを知りたいことがよくあります。 ここでカウントするように-私は8の数を学びました-エリアは19であり、7の数をカウントしました-エリアは7です（注釈の写真を参照）。
そうすることで、画像上で追加のパスを使用せざるを得なくなります。これを回避することをお勧めします-実装の効率を高めるためです。 計画どおり、このトピックでは、追加のパスなしでオブジェクトの幾何学的特性を計算することについて説明します。
また、フォームファクターとグイドグランディローズ、正方形と長方形の違い、星の形も違います。
記事の前の部分：
パート1
オブジェクトのカウントと幾何学的特徴の計算
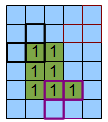最初に、この領域を扱います。 前の記事では、ABCマスクの5つの位置が考慮されました。5番目の位置には、2つのマークされた接続領域の結合が含まれていました。
次のロジックをソースコードに追加します-各条件付き位置に：
- 位置1から5の場合：現在のラベルを持つオブジェクトの領域を1つ増やす必要があります。
- さらに、5番目の位置では、同等の番号BとCの下の領域を結合するときに、S（B）= S（B）+ S©を実行します。
簡潔にするために、各位置に新しい行のみを含むソーススクリプトコードを提供します。
A == 0の場合
elseif B == 0＆C == 0 then
/.../
二乗（cur）=二乗（cur）+ 1;
elseif B〜 = 0＆C == 0 then
/.../
二乗（B）=二乗（B）+ 1;
elseif B == 0＆C〜= 0 then
/.../
正方形©=正方形©+ 1;
elseif B〜 = 0＆C〜= 0 then
二乗（B）=二乗（B）+ 1;
B == Cの場合
Im（i、j）= B;
他に
/.../
正方形（B）=正方形（B）+正方形©;
正方形©= 0;
終わり
/.../
終わり
*このソースコードは、 ソースコードハイライターで強調表示されました。
リスト1-マークされたオブジェクトの面積を計算するためのスクリプトコードの変更。
オブジェクトの周囲を数えるのはもう少し複雑です。 B == 0またはC == 0の場合のエリアの状況のように
また、境界線を増やす必要があります。 ただし、これでは十分ではありません。 別のABCマスクを導入します-同じコーナー（図では黒いマスク）、ただし180度反転（図では紫のマスク）。 これにより、さらに3つの可能性のある状況が追加されますが、それらはポジション5の枠組み内でのみ考慮されるべきです。
elseif B〜 = 0＆C〜= 0 then
二乗（B）=二乗（B）+ 1;
B == Cの場合
Im（i、j）= B;
他に
Im（i、j）= B;
Im（Im == C）= B;
正方形（B）=正方形（B）+正方形©;
正方形©= 0;
Perimetrs（B）= Perimetrs（B）+ Perimetrs©;
Perimetrs©= 0;
終わり
A = Im（i、j）;
kn = j + 1;
kn> nの場合
kn = n;
Bは0です。
他に
B = Im（i、kn）;
終わり
km = i + 1;
km> mの場合
km = m;
Cは0です。
他に
C = Im（km、j）;
終わり
B == 0＆C == 0の場合
ペリメーター（A）=ペリメーター（A）+ 1;
elseif B〜 = 0＆C == 0 then
ペリメーター（A）=ペリメーター（A）+ 1;
elseif B == 0＆C〜= 0 then
ペリメーター（A）=ペリメーター（A）+ 1;
終わり
終わり
*このソースコードは、 ソースコードハイライターで強調表示されました。
リスト2-オブジェクトの境界を計算するためのスクリプトコードの変更。
この原理を要約すると、ABCマスクとオブジェクトマーキングアルゴリズムを使用して、領域をマージするときに線形性を持つ幾何学的特徴を計算できる、つまり、オブジェクト3を2つの部分で構成すると考えることができます：Obj3 = Obj1 + Obj2、その符号F （Obj3）= F（Obj1）+ F（Obj2）。 この例としては、オブジェクトの重心があります。
フォームファクター
学校のベンチから、誰もが幾何学図形については、面積と周囲を計算できることを知っています。 たとえば、 円の場合、式は次のようになります
興味深い比率（3）を考えてください。これは、面積と周囲の両方を組み合わせたものです-これはフォームファクターのタイプの1つです。 円の面積と周囲の対応する式をそれに代入すると、任意の半径の円の形状係数が0であることを理解するのは簡単です。
ただし、円の場合、すべてが非常に単純ですが、より複雑な形状はどうなりますか？ この記事では、いわゆるグイドグランディローズについて検討します（図1）。
図1-グイドグランディの多くのバラ。
実装を簡単にするために、極座標系を混乱させないように、デカルト座標の元の式を再編集しました（4） が、元の構成規則とは異なりますが、結果は同様であり、目的に適しています（図1）。
バラの変数パラメータに応じて、フォームファクター（3）はどのように動作しますか？ これを図2のグラフに示します。
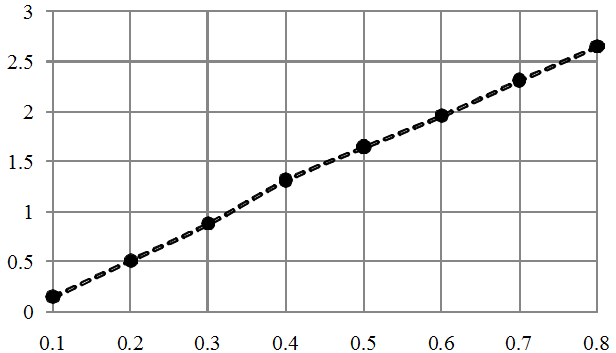
図2 -Guido Grandiのフォームファクター（3）は、垂直軸に沿った変数パラメーターに応じて、水平軸に沿って上昇します。
線形依存性が明らかになり、分析レコードがあり、この式は非常に簡単に導出できると確信しています。 読者にとってはちょっとしたパズルにしましょう。
その結果、面積と周囲の単純な比率を使用して、図を識別できる標識を取得しました-認識します。 実際には、この記号は記号のベクトルの多くの1つにすぎません。 それは、相似歪み（類似性、スケール）には耐性がありますが、バラの半径を変化させながら、2値化と量子化によって生成された図形の輪郭の誤差のために+（-）0.15の精度で計算されます。
次に、この機能を使用して正方形と長方形を区別する方法を見てみましょう。 簡潔にするために、図のみを示します-図3。
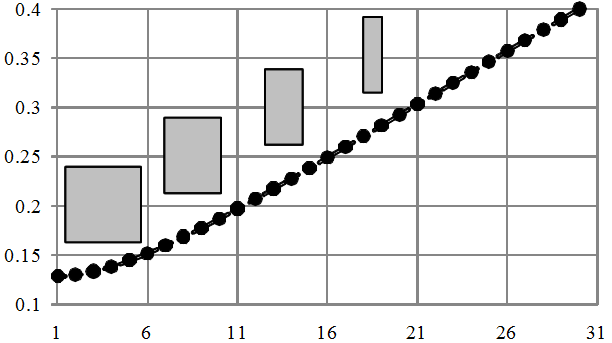
図3-正方形を長方形に描くときのフォームファクターの変化。
ここでは、依存関係はすでに非線形であり、これは分析式から明らかです。
図形のコンパクトさを含む、フォームの多くの同様の発見的要因があります。
おわりに
ここでは、実験用のSciLabスクリプトをダウンロードできます。これには以下が含まれます。
アーカイブは、最初のコメントに示されているパスワードで暗号化されています。このような不便をおpoびしますが、これは、通常、コメントがコピーされないコピー貼り付け者から保護するためです。
読んでくださった皆さんのおかげで、私はあなたのコメントを待っています。 フォームファクターが記述されている文献に誰かが精通している場合-リンクをお願いしますが、出版前に自己批判を得るために何かを見つけることができませんでした。
UPD： 06/06 / 11、15 ： 28