編集距離、またはレーベンシュタイン距離は、2行の「類似性」を判断できるメトリックです。1つの行を別の行に変換するために必要な、1つの文字の挿入、1つの文字の削除、1つの文字の別の文字への置換の最小回数です。 この記事では、速度を大幅に低下させることなく、少量のメモリを使用して編集距離を計算する方法の概要を説明します。 このアプローチは、「類似性」の評価だけでなく、1行を別の行に転送する一連の変更を受信するときに、大きな行(10 5文字程度、つまり実際にはテキスト)に適用できます。
わずかな形式化
2つの線S 1とS 2があるとします。 次の操作を使用して、一方をもう一方に転送します(最初から2番目に移動し、操作が対称であることを示すのは簡単です)。
- I:任意の場所に文字を挿入します。
- D:任意の位置から文字を削除します。
- R:キャラクターを別のキャラクターに置き換える。
次に、d(S 1 、S 2 )は、S 1をS 2に転送するためのI / D / R操作の最小数であり、編集指示は、パラメーターと一緒に変換する操作のリストです。
この問題はWagner – Fisherアルゴリズムで簡単に解決できますが、編集処方を復元するにはO(| S 1 | * | S 2 |)メモリセルが必要です。 「最適化」はアルゴリズムに基づいているため、アルゴリズム自体の概要を簡単に説明します。
ワーグナーフィッシャーアルゴリズム
必要な距離は、サブストリングS 1 [0..M]およびS 2 [0..N]の編集距離を見つける補助関数D(M、N)によって形成されます。 その後、編集距離の合計は、完全な長さの部分文字列の距離に等しくなります:d(S 1 、S 2 )= D S 1 、S 2 (M、N)。
自明の事実は次のとおりです。
D(0,0)= 0。
実際、空の行は同じです。
また、次の意味も明確です。
D(i、0)= i;
D(0、j)= j
実際、適切な数の文字を追加することにより、どの行も空になることがあります。他の操作ではスコアが増加するだけです。
一般的な場合、もう少し複雑です:
S 1 [i] = S 2 [j]の場合、D(i、j)= D(i-1、j-1)
それ以外の場合、D(i、j)= min(D(i-1、j)、D(i、j-1)、D(i-1、j-1))+ 1。
この場合、どちらがより収益性が高いかを選択します:文字を削除する(D(i-1、j))、追加する(D(i、j-1))、または置き換える(D(i-1、j-1))。
推定値を取得するためのアルゴリズムは、現在の(D(i、*))と前の(D(i-1、*))の2列を超えるメモリを必要としないことは容易に理解できます。 ただし、編集規定を復元するには、完全なマトリックスが必要です。 マトリックス(M、N)の右下隅から開始して、左上の各ステップで、最小3つの値を探します。
- 最小の場合(D(i-1、j)+ 1)、文字S 1 [i]の削除を追加し、(i-1、j)に進みます。
- 最小の場合(D(i、j-1)+ 1)、シンボルS 1 [i]の挿入を追加し、(i、j-1)に進みます。
- 最小の場合(D(i-1、j-1)+ m)、ここでm = 1、S 1 [i]!= S 2 [j]、それ以外の場合m = 0。 その後、(i-1、j-1)に進み、m = 1の場合は置換を追加します。
その結果、O(| S 1 | * | S 2 |)時間とO(| S 1 | * | S 2 |)メモリーが必要です。
一般的な議論
このメソッドを作成するための前提条件は単純な事実です。実際のシステムでは、メモリは時間よりも高価です。 実際、長さが2 16文字の文字列の場合、約2 32の計算操作(最新の容量では計算の10秒以内に収まります)と2 32のメモリが必要です。これはほとんどの場合、既にマシンの物理メモリよりも大きいです。
メモリの線形量(2 * | S 1 |)を使用して距離を推定する方法のアイデアは、表面にあり、編集処方の計算にそれを正しく転送するために残っています。
カウンター計算方法(Hirschbergアルゴリズム)
再帰を使用して、タスクをサブタスクに分割します。各サブタスクは多くのメモリを必要としません。 さらにスケッチするために、文字列の初期値をいくつか取ります。
S 1 = ACGTACGTACGT、
S 2 = AGTACCTACCGT。
それのように見えますか? しかし、「目で」別のものに書き換えることはそれほど明白ではありません。 ちなみに、文字は偶然に選択されたものではありません-これらは窒素塩基(A、T、G、C)、DNAコンポーネントです:編集距離推定法は、突然変異を評価するために生物学で積極的に使用されています。
次に、元の未入力のマトリックスが次のように表示されます(正確に表示され、必要なデータのみを保存します)。

各セルには、編集距離の値が必要です。
元のタスクをサブタスクに分割し、2番目の行を2つの等しい(またはほぼ等しい)部分に分割し、パーティションの場所を覚えて、Wagner-Fisherで行ったのとまったく同じ方法でマトリックスを埋め始めます。
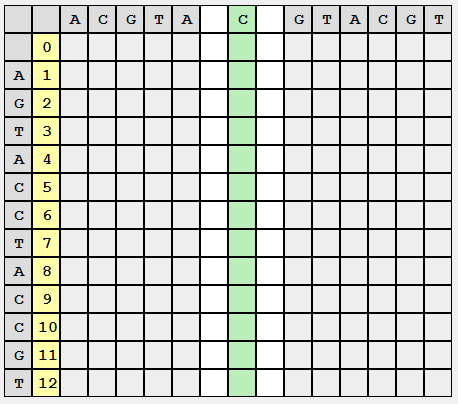
記入するとき、D(i、j)の値を計算するときに、左から右へ、上から下へ移動して、前の列を保存しません。D(i-1、j)の値は削除できます。

同様に、パーティションの右側を埋めます。 ここでは、右から左、上から下に移動します。

だから会った。 商を組み合わせることで、一般的な問題の解決策の一部を取得できます。 左右の列で取得した値を要約し、最小値を選択します。

この組み合わせはどういう意味ですか? 最初の行と2番目の行の前半を組み合わせてから、最初の行と2番目の行の後半を組み合わせようとしました。 合計により、最初の行を変更する操作の数を取得できるため、2番目の行の前半と後半(つまり、2番目の行)が連結されます...これは、編集距離の値を取得したことを意味します! しかし、この結果を簡単に達成できた可能性があるため、喜ぶには時期尚早です(上記の方法)。
しかし、別の角度から(文字通り)絵を見ると、別の重要な事実が得られました。最初の行を2つの半分に「カット」して、対応するペアが編集距離d(S 1 1 、S 2 1 ) + d(S 1 2 、S 2 2 )= d(S 1 、S 2 )。 最小値が配置されている行(マトリックス内)は目的のパーティションS 1であり、このパーティションは編集処方箋を発行するために送信されます。
同様に、結果の部分文字列S 1 1とS 2 1に対して既にタスクを分割します(2番目のペアも忘れません)。
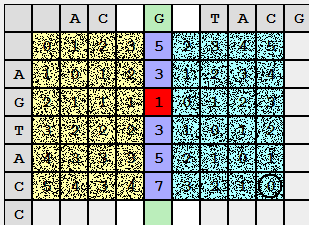
長さが1を超える部分文字列S 1がない場合、除算を完了します。

パーティションのリストを取得します。各サブストリングS 1 (垂直に見える)は、対応するサブストリングS 2 (水平方向)に対する変更の最小推定値を示します。
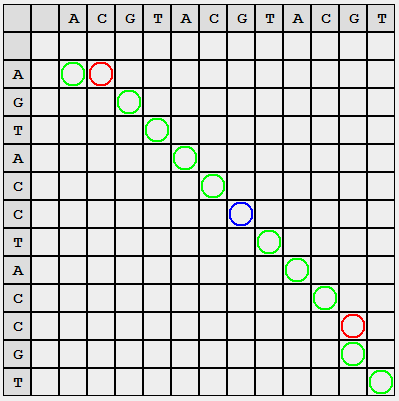
便宜上、マークを色で塗りつぶしました。緑は選択した位置の行の文字ごとの一致、青は置換の必要性、赤は削除または追加を意味します。 「赤」の円が同じ行/列にあることに気付くのは簡単です(タスクには注意が必要です:これが何から来るのかを説明してください)。
より便利な形式では、結果は次のように書くことができます(赤いストローク-一致する文字、シフトは黒い水平で示されます):

アルゴリズム分析
メモリー:各ステップで、1列d(i、*)およびパーティションのセットS 1のみを記憶する必要があります。 合計O(| S 1 | + | S 2 |)。 つまり、2次ボリュームの代わりに、線形ボリュームを取得します。
時間:列tのS [0..N]の各パーティションは、サブストリングS [0..t]およびS [t..N]の処理を生成します。 パーティションNの合計。各パーティション(S 1 [i..j]、S 1 [k..n])を処理する場合、(j-i)x(n-k)操作が必要です。 部分文字列の最悪ケースの推定値を合計すると、2 * | S 1 | * | S 2 | 操作。 乗算定数は変更されましたが、アルゴリズムの実行時間は2次のままでした。
そこで、線形のメモリ量と速度のわずかな損失を使用して問題を解決しましたが、この場合は成功と見なすことができます。
[*] Wikipedia: Hirschbergアルゴリズム 。