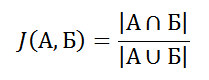
つまり、交点の要素数を和集合の要素数で割ったものです。 この推定値はJaccard係数(Jaccard、したがって「J」)と呼ばれ、セットに共通の要素がない場合は係数はゼロ、セットが等しい場合は係数は1、そうでない場合は値は中間になります。
それを数えるには?
文字列セットのペアに対してこの係数を計算する方法を考えてみましょう。あるテキストが別のテキストにどれだけ似ているかを調べることにしたとしましょう。 最初に、テキストを個別の単語に分割する必要があります。これらはセットの要素になります。次に、交差点と結合のサイズを何らかの方法で計算する必要があります。
通常、最後の2つの操作を効果的に実行するために、セットはキーに関連付けられた値のないハッシュテーブルとして提示されます;このような構造は非常に迅速に機能します。 テーブルの構造はO(n)で、2つ必要です。交差の計算はO(n)で、結合の計算もO(n)です。ここで、nはテキスト内の単語の数です。 すべてがうまくいくように見えますが、タスクを複雑にしましょう。
データベースに一連のテキストデータ(投稿、コメントなど)が格納されており、新しいエントリを追加するときに、既存のものとあまりにも似たものを選別する必要があるとします。 この場合、すべてのドキュメントをダウンロードし、それらのハッシュテーブルを作成する必要があります。 これはかなり迅速に行われますが、操作の数はドキュメントのサイズとその数に直接依存します。
最後の問題は、たとえば同じSphinxでインデックスを作成することで解決できます。その後、比較のために、共通の単語の特定のサブセットを持つドキュメントのみをアップロードできます。 これはうまく機能しますが、小さなドキュメントに対してのみ、大きなドキュメントに対しては、テストサブセットが大きくなりすぎます。 最初の解決策とこの派生問題を扱います。
キーMinHashのアイデア
2つのセットA、B、およびこれらのセットの要素のハッシュを計算できるハッシュ関数hがあるとします。 次に、関数h min (S)を定義します。これは、セットSのすべてのメンバーの関数hを計算し、その最小値を返します。 ここで、異なるセットのペアのh min (A)とh min (B)の計算を開始しましょう。問題は、h min (A)= h min (B)になる確率はどれくらいですか?
考えてみると、この確率は集合の交点のサイズに比例するはずです-一般的な用語がない場合はゼロになる傾向があり、集合が等しい場合は統一される傾向があり、中間の場合は中間のどこかになります。 何にも似ていませんか? ええ、そうです、これはJ(A、B)-ジャカード係数です!
問題は、2つのテキストについてh min (A)とh min (B)を単純に計算し、値を比較すると、何も得られないためです。 等しいか等しくないかの2つのオプションしかありません。 真理に近いJ(A、B)を計算するために、何らかの方法でセットに関する十分な量の統計を取得する必要があります。 これは1つの関数hの代わりに単純に行われ、いくつかの独立したハッシュ関数、またはk関数を導入します。

ここで、εは必要な最大誤差です。 そのため、J(A、B)を0.1以下の誤差で計算するには、100個のハッシュ関数が必要です(少数ではありません)。 プラスは何ですか?
第一に、いわゆるシグネチャH min (S)を計算できます。 セットSのすべてのハッシュ関数の最小値。計算の複雑さはハッシュテーブルを構築する場合よりも大きくなりますが、それでも線形であり、データベースに追加する場合など、各ドキュメントに対してこれを1回だけ行う必要があります。署名のみ。
第二に、お気づきかもしれませんが、署名は特定の最大エラー値に対して固定サイズです。 任意のサイズの任意の2つのセットを比較するには、一定数の操作を実行する必要があります。 さらに、理論的には、署名の方がはるかに便利です。 「理論上」というのは、それらのインデックス付けがリレーショナルデータベースにあまり適合せず、フルテキストエンジンでもあまり良くないからです。 少なくとも私はそれを美しくする方法を理解できませんでした。
おもちゃの実装
いつものように、ハッシュ関数のファミリーが必要です:
function Hash(size) { var seed = Math.floor(Math.random() * size) + 32; return function (string) { var result = 1; for (var i = 0; i < string.length; ++i) result = (seed * result + string.charCodeAt(i)) & 0xFFFFFFFF; return result; }; }
MinHash自体:
function MinHash(max_error) { var function_count = Math.round(1 / (max_error * max_error)); var functions = []; for (var i = 0; i < function_count; ++i) functions[i] = Hash(function_count); function find_min(set, function_) { var min = 0xFFFFFFFF; for (var i = 0; i < set.length; ++i) { var hash = function_(set[i]); if (hash < min) min = hash; } return min; } function signature(set) { var result = []; for (var i = 0; i < function_count; ++i) result[i] = find_min(set, functions[i]); return result; } function similarity(sig_a, sig_b) { var equal_count = 0; for (var i = 0; i < function_count; ++i) if (sig_a[i] == sig_b[i]) ++equal_count; return equal_count / function_count; } return {signature: signature, similarity: similarity}; }
使用例:
var set_a = ['apple', 'orange']; var set_b = ['apple', 'peach']; var min_hash = MinHash(0.05); var sig_a = min_hash.signature(set_a); var sig_b = min_hash.signature(set_b); alert(min_hash.similarity(sig_a, sig_b));
微妙な瞬間
実際には、実際のハッシュ関数は完全ではないため、精度はわずかに低くなります。 あなたはこれを我慢するか、いくつかの追加機能を導入することができますが、2、3個はあまり役に立ちません。
何らかの理由で、関数によって生成されるビット数が何であるかはどこにも言及されていません。 理論的には、この量は、入力値のすべての可能なバリエーションを表すようなものでなければなりません。 たとえば、英語では約250 000ワードなので、約18ビットで十分です。 しかし、これも安全にプレイし、いくつかのビットを追加することをお勧めします。
ここでテキストを比較できます 。 ご清聴ありがとうございました、すぐに会いましょう。
PS HabraStorageで写真をロードするとき、または私だけでエラーが発生しますか?