はじめに
RMQの問題は、スポーツおよびアプリケーションプログラミングでは非常に一般的です。 誰もこの興味深いトピックをHabréで言及していないのは驚くべきことです。 ギャップを埋めようとします。
頭字語RMQはRange Minimum(Maximum)Query-配列内のセグメントの最小(最大)を照会します。 明確にするために、最小値を取る操作を検討します。
配列A [1..n]を与えます。 「i番目の要素からj番目の要素までの間隔の最小値を見つける」という形式の要求に応答できる必要があります。
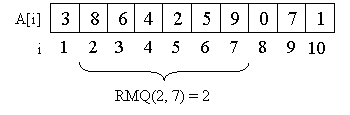
例として、配列A = {3、8、6、4、2、5、9、0、7、1}を考えます。
たとえば、2番目の要素から7番目の要素までのセグメントの最小値は2、つまりRMQ(2、7)= 2です。
明らかな決定が思い浮かびます。必要なセグメントにある配列のすべての要素を調べるだけで、各要求に対する答えが見つかります。 ただし、このようなソリューションは最も効果的ではありません。 実際、最悪の場合、O(n)個の要素、つまり このアルゴリズムの時間の複雑さは、要求ごとにO(n)です。 ただし、問題はより効率的に解決できます。
問題文
まず、問題の説明を明確にします。
記事のタイトルで静的という言葉は何を意味しますか? RMQのタスクには、配列の要素を変更する機能が含まれることがあります。 つまり、要素を変更する機能、またはセグメント内の要素を変更する機能(たとえば、サブセグメント内のすべての要素を3増やす)が、最小テイクリクエストに追加されます。 ダイナミック RMQと呼ばれるこのバージョンの問題は、以降の記事で検討します。
ここで、RMQタスクはオフラインバージョンとオンラインバージョンに分かれていることに注意してください。 オフラインオプションでは、最初にすべてのリクエストを取得し、何らかの方法でリクエストを分析してから、リクエストに回答することができます。 オンラインの声明では、リクエストは順番に与えられます。 次の要求は、前の要求への答えの後にのみ来ます。 オンラインインストールでRMQを解決すると、 オフライン RMQのソリューションがすぐに得られますが、 オンラインインストールには適用できないオフライン RMQのより効果的なソリューションがある場合があります。
この記事では、 静的なオンライン RMQについて説明します。
前処理時間
アルゴリズムの有効性を評価するために、もう1つの時間特性である前処理時間を導入します。 その中で、準備の時間、つまり 要求に応答するために必要ないくつかの情報の事前計算。
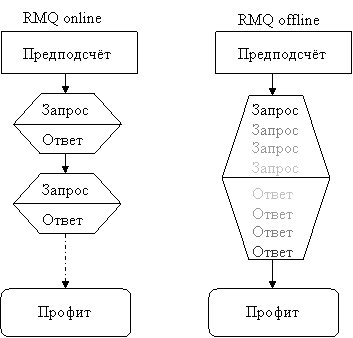
どうして前処理を個別に分離する必要があるのでしょうか? しかし、なぜ。 この問題に対するもう1つの解決策を示します。
クエリへの応答を開始する前に、各セグメントの答えを取り、単純に計算してください! つまり 配列P [n] [n]を構築します(将来、Cのような構文を使用しますが、実装を容易にするために配列Aに1から番号を付けます)。ここで、P [i] [j]はiからjの間隔の最小値に等しくなります そして、少なくともO(n 3 )に対してこの配列をカウントします-最も愚かな方法で、各セグメントのすべての要素を調べます。 なぜこれを行うのですか? クエリの数qがn 3よりもはるかに大きいとします。 このアルゴリズムの合計動作時間は、O(n 3 )+ q * O(1)= O(q)、つまり 全体の前処理の時間は、アルゴリズムの全体的な時間に影響しません。 しかし、O(n)ではなくO(1)の時間でリクエストに応答することを学びました。 O(q)がO(qn)よりも優れていることは明らかです。
一方、q <n 3の場合、前処理時間が役割を果たします。上記のアルゴリズムでは、O(n 3 )です。残念ながら、Oに短縮(方法を考える)することはできますが、長すぎます。 (n 2 )。
この時点から、アルゴリズムの時間的特性を(P(n)、Q(n))として示します。ここで、P(n)は事前計算する時間、Q(n)は1つの要求に応答する時間です。
したがって、2つのアルゴリズムがあります。 1つは(O(1)、O(n))で機能し、2つ目は(O(n 2 )、O(1))で機能します。 (O(nlogn)、O(1))で問題を解決する方法を学びます。ここで、lognはnの2進対数です。
叙情的な余談。 対数の基数として任意の数値を使用できることに注意してください。 log a nは常にlog b nとは正確に一定回数異なります。 定数は、学校代数コースから思い出すように、log a bです。
そこで、次のステップに進みました。
スパーステーブル、またはスパーステーブル
スパーステーブルは、ST [k] [i]が半間隔[A [i]、A [i + 2 k ])で最小になるようなテーブルST [] []です。 つまり、長さが2の累乗であるすべてのセグメントの最小値が含まれます。
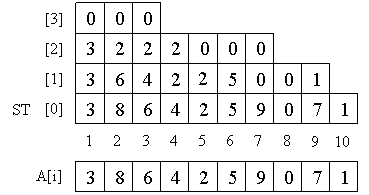
配列ST [k] [i]を次のようにカウントします。 ST [0]が単なる配列Aであることは明らかです。次に、clearプロパティを使用します。
ST [k] [i] = min(ST [k-1] [i]、ST [k-1] [i + 2 k-1 ])。 彼のおかげで、最初にST [1]、次にST [2]などを計算できます。
テーブルにO(nlogn)要素があることに注意してください。kの値が大きいと、半区間の長さが配列全体の長さより長くなり、対応する値を格納する意味がないため、レベル番号はlogn以下でなければなりません。 各レベルでO(n)個の要素。
再び叙情的な余談:配列の未使用の要素がまだたくさんあることに気付くのは簡単です。 メモリを無駄にしないために、テーブルを異なる方法で保存することは価値がありますか? 実装の未使用メモリの量を推定します。 未使用要素のi番目の行-2 i -1。したがって、未使用の合計はΣ(2 i -1)= O(2 logn )= O(n)のままです。つまり、いずれの場合も次数O(nlogn)が必要です。 -O(n)= O(nlogn)スパーステーブルを格納する場所。 したがって、未使用のアイテムを心配することはできません。
そして今、主な質問:なぜこれをすべて考慮したのですか? 配列のセグメントは、長さ2の2つの重複するサブセグメントに分割されることに注意してください。

RMQ(i、j)を計算する簡単な式が得られます。 k = log(j-i + 1)の場合、RMQ(i、j)= min(ST(i、k)、ST(j-2 k + 1、k))。 したがって、アルゴリズムは(O(nlogn)、O(1))で取得します。 やった!
...ほとんど入手できます。 O(1)に向かう対数をどのように取りますか? それを計算する最も簡単な方法は、nを超えないすべての値に対してもです。 前処理の漸近的な動作がこれから変化しないことは明らかです。
次は?
そして、後続の記事では、このタスクのさまざまなバリエーションと、それに関連する次のようなプロットについて検討します。
- セグメントのツリー
- 間隔変更
- セグメントの2次元ツリー
- 隣接するRSQ問題
- フェンウィックツリー
- LCAタスク
- RMQ問題の永続的な声明
- ...多くの興味深いもの...
- そして最も魅力的なもの:Farah-Colton and BenderアルゴリズムとRMQ-> LCA-> RMQ±1変換。これにより、(O(n)、O(1))のRMQ問題を解決できます。
詳細については、たとえば、T。Cormen、C。Leiserson、およびR. Rivestの巧妙な本「Algorithms:construction and analysis」に問い合わせてください。
他のトピックは、後続のトピックに表示されます。
ご清聴ありがとうございました。