注釈
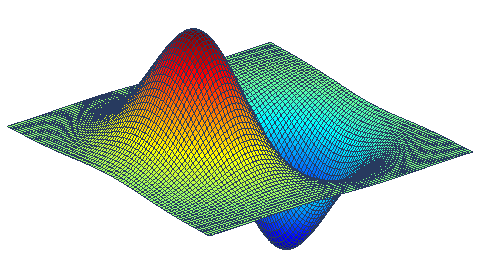
Canny Boundary Detectorの記事では、既にコメントで書いたように、勾配の検索場所でアルゴリズムの本質が歪んで失われています。 このために、そこではSobelのカーネルが使用されていますが、Cannyはそのことについてまったく言及していません。 輪郭アルゴリズムをより高速に動作させるための修正を書きました。 また、この記事は、「イメージグラデーションについて」の執筆の続きと考えることもできます。
この記事では、潤滑剤コアの最適な離散化ステップの選択に関する問題については触れていません。
背景
- 多くの場合、画像の輝度関数の勾配を計算する前に、安定した結果を得るために、ガウスフィルターを使用したノイズフィルターを使用します。つまり、予備潤滑を実行します。
- 次に、導関数の差分近似を使用して、勾配成分が検出されます。
サイズNxNポイントのカーネルを使用して潤滑を行い、軸に沿った導関数を計算するための差分テンプレートは1xKおよびKx1です。 画像サイズはMxMと等しく設定されます 。
簡単にするために、乗算のみを考慮し、シーケンス「Smaz-> Gradient」では、 N ^ 2 * M ^ 2 + 2 * K * M ^ 2 =(N ^ 2 + 2 * K)* M ^ 2演算が必要になります。
ただし、既知の式
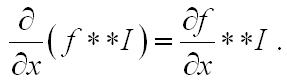
これを使用すると、桁数を減らすことができます。 彼女は何について話しているのですか? -原則として、最初に潤滑を行ってから画像を区別する必要がないという事実について。 グリースfのコアと畳み込みを区別できます。 始めましょう。
カーネル分離
2次元のガウス関数を見てみましょう。
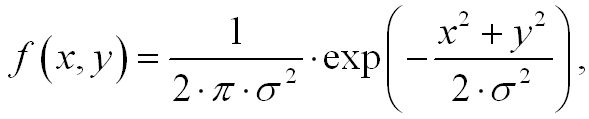
xに関するその導関数は次のように記述されます。
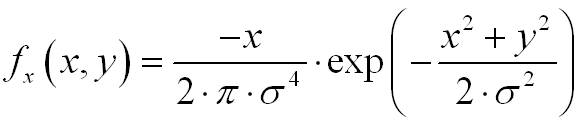
MatLabのコードを実行すると、このすばらしい派生物を取得できます。
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
sigma = 1.4; x = -3*sigma:0.1:3*sigma y = x; [x,y] = meshgrid(x,y); Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 ); figure; surf(Fx1) * This source code was highlighted with Source Code Highlighter .
このようなカーネルを持つフィルターはCannyフィルターと呼ばれることもあり、カーネルはCannyカーネルと呼ばれます。これは、他の演算子とともに微分を近似します。 この機会に、私は非常に図解されたメモを共有します。
導関数は座標によって分離可能であることに注意してください。これは、ぼやけた画像の勾配を計算するための行-列アルゴリズムを実装できることを意味します。

行-列アルゴリズムの場合、操作の数を計算します。
yに関する導関数を取得するには:
- サイズ1xK1のウィンドウで行のガウス画像Iを処理し、 K * M ^ 2の乗算の画像I1を取得します(カーネルの正規化を忘れないでください)。
- サイズがK1x1のカーネルを使用して、画像I1を行単位で処理します。
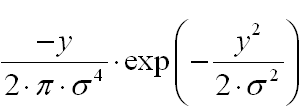
(サンプルの合計が0になるようにカーネルの離散化ステップを選択することを忘れないでください)
このような操作には、 K * M ^ 2の乗算が必要です。
xに関する導関数を取得するアルゴリズムは類似しており、取得する操作の数を合計すると、ぼかし勾配の成分を計算するために4 * K1 * M ^ 2が必要です。
有効性
説明した最適化の有効性は、比率によって定量化できます。
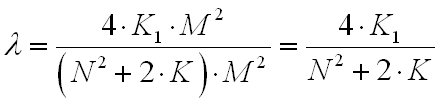
効果はウィンドウのサイズにのみ依存し、画像のサイズには依存しないことが判明しました。
サイズN = 5のカーネルを単純なアルゴリズムの潤滑に使用し、1次近似(カーネル[-1 1]および[-1 1] ') -K = 2を使用して導関数を計算します。
最適化された行-列アルゴリズムの場合、K1 = 5に設定します。その後、λ= 20/29 = 0.68に設定します。
効率λ<1-シーケンス「Lubric-Gradient」を計算するときに、算術演算の数を減らすことができました。