👵 🛐 👦 サブセグメントダイナミクス：基本的なことと「1つが良いと2つが良い」 🐔 👩🏻‍🚒 😘

こんばんは

この投稿では、サンクトペテルブルクで開催された都市コンピュータサイエンスオリンピアードの実地ツアーの問題B「オークス」を分析します。

サブセグメントによる動的プログラミングのこの問題と解決策のアイデアは、1人ではなく2人の話者を数える方が便利であるという点で興味深いものです。興味がある場合（ダイナミクスの無知は解放されませんが、より困難になります）-ようこそ。

状態

まず、問題の状態を確認できます。ここにはテストがあります（min.usからダウンロードできるのは条件のみです）。

凡例を折り畳んだ後、次のタスクが残ります。

n個（2 <= n <= 200）のオークがあり、それぞれに高さ（1〜1000の整数）があります。
次の場合に、シーケンスからオークを削除できます。
- または、両方の隣人より厳密に小さい
- または厳密にそれらの多く
たとえば、次の図では、「オーク」が緑色で強調表示されており、削除できます。

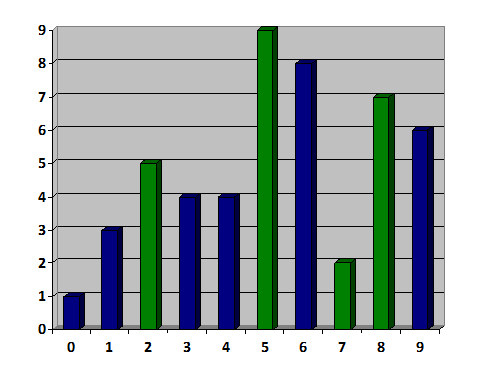
最小限の操作で、シーケンスを厳密に増加しないシーケンスに変換する必要があります。削除シーケンスも推測する必要があります。たとえば、次のように：

必要に応じて、あなたはそれについて考えることができます（投稿の名前が教えてくれます）。

主なアイデア

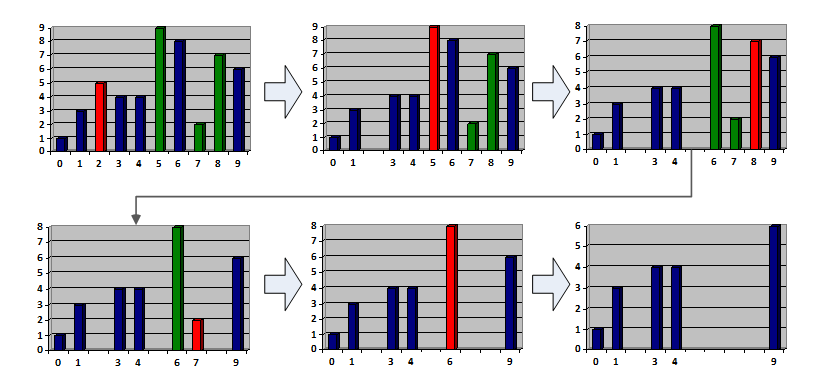
あなたがタグから推測するかもしれないように-ソリューションは特定のダイナミックです。動的プログラミングが何であるかを忘れた、または知らなかった場合は、お知らせします。ダイナミクスのアイデアは、非常に小さな例（たとえば、1つのツリー）で答えは明らか（何も表示されない）ですが、大きなものでは、いくつかの小さな独立したサブタスクの解決策を知っていれば解決策を得ることができます。この時点で、ダイナミクスは誘導を非常に連想させます。たとえば、10本の木をより小さなものに減らす方法はありますか？すでに答えがわかっていると仮定します（使用しませんが、これを想像すると便利です）。 2つの極端なツリーとその中のいくつかがあります。この真ん中のツリーを繰り返してみましょう（一般的に、境界線の間の高さにあるすべてのツリー-それ以外の場合は残すことはできません）：

すべての操作が左側または右側のいずれかで実行されることがわかります。したがって、それらは互いに依存しません。そのため、2つの独立したサブタスクに分割されました。私たちの大規模なセグメントでリラックス（最高の選択）することができます。

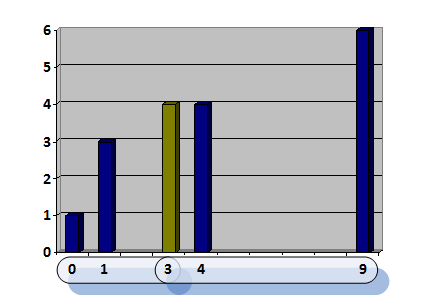
そして、境界線の間に木がない場合（たとえば、木4と9）はどうしますか？ここでは、この場合、区間のすべての木を切り倒す必要があることを理解しています。問題は、どのような順序ですか？貪欲なアルゴリズムを作成する誘惑があります：最初に出会うまでツリーを切り倒します。しかし、それは間違っています：

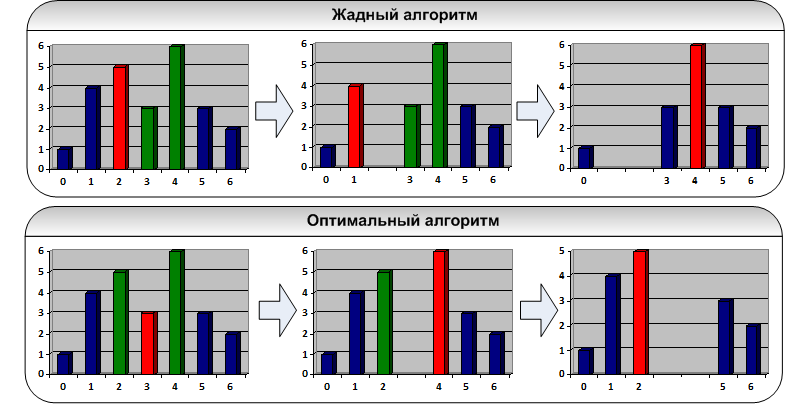
「最後の2ステップで検索を開始する」などのスタイルでさまざまな最適化を行うべきではないことは明らかだと思います。これはすべて、大きなランダムテストで中断します。

よりスマートなものが必要です。投稿のタイトルをもう一度見て、サブセグメントごとに非常によく似たダイナミクスを見つけます。2本以下のツリーでは、削除する必要はまったくありません。さらに、ツリーを整理する必要があります。ツリーを最後に削除し、左と右の2つのサブタスクを受け取ったことに注意してください。唯一の違いは、このツリーを最後に削除できることを確認する必要があることです（間隔の境界が隣接する場合）。

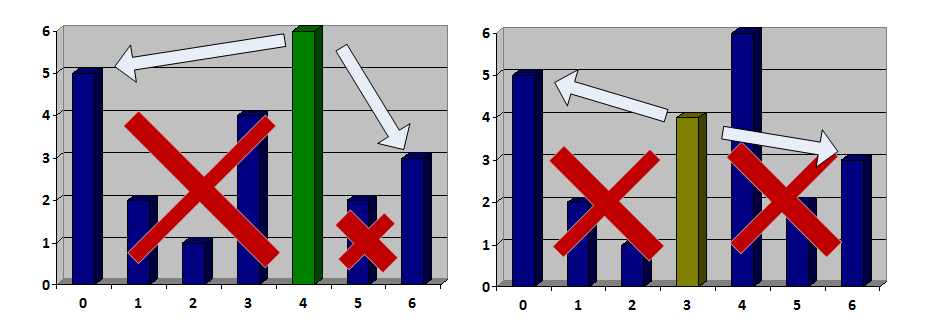
たとえば、ツリー4は最後に削除できますが、ツリー3は削除できません。

回答の回復

答えは古典的な方法によって復元されます-各状態（最適な答えに到達した）から配列への最適な遷移を覚えてから、最後から進みます。サブセグメントによって再帰的にダイナミクスにリカバリを書き込むと便利です。

回答の回復

vector < int > ans ; //   
      

        
        
        
      

     // a  b -  ,       
      

        
        
        
      

     void deleteAll ( int a, int b ) { 
      

        
        
        
      

     assert ( del [ a ] [ b ] >= 0 ) ; 
      

        
        
        
      

     if ( del [ a ] [ b ] == a ) return ; 
      

        
        
        
      

     deleteAll ( a, del [ a ] [ b ] ) ; 
      

        
        
        
      

     deleteAll ( del [ a ] [ b ] , b ) ; 
      

        
        
        
      

     ans. push_back ( del [ a ] [ b ] ) ; 
      

        
        
        
      

     } 
      

        
        
        
      

     
      

        
        
        
      

     //  
      

        
        
        
      

     void restoreAns ( int a, int b ) { 
      

        
        
        
      

     assert ( fr [ a ] [ b ] >= 0 ) ; 
      

        
        
        
      

     if ( fr [ a ] [ b ] == a ) { 
      

        
        
        
      

     deleteAll ( a, b ) ; 
      

        
        
        
      

     return ; 
      

        
        
        
      

     } 
      

        
        
        
      

     restoreAns ( a, fr [ a ] [ b ] ) ; 
      

        
        
        
      

     restoreAns ( fr [ a ] [ b ] , b ) ; 
      

        
        
        
      

     }

作業時間

合計で、各ダイナミクスのO（n ² ）状態があります（各サブセグメントに1つ）。各ダイナミクスで、遷移はO（n）で行われます-間隔内でツリーを反復処理します。答えを復元するとき、各州を1回しか訪れません。正方形であることがわかりますが、漸近的に（無限に大きいnでは無限に小さい）立方体よりも小さいため、無視できます。

合計動作時間はO（n ³ ）で、 n = 200でO（8 * 10 ⁶ ）になり 、即座に解決します。それも私たちに合っています。

書き方

最初に、データを配列/ベクトルに読み込む必要があります。あなたはそれを行う方法を知っています。

最初のスピーカー

次に、すべてのツリーを削除するためにダイナミクスを計算する必要があります。間隔（a、b）のすべてのツリーを削除することが不可能で、最後のツリーの数が異なる場合、配列int del [a] [b] -- 1に格納します。

サブセグメントを列挙するには、次の2つのサイクルを記述したいと思います。

for ( int left = 0 ; left < n ; left ++ ) 
      

        
        
        
      

     for ( int right = left ; right < n ; right ++ ) { 
      

        
        
        
      

     // ... 
      

        
        
        
      

     }

しかし、これは根本的に間違っています。ダイナミクスの遷移は、「より小さい」サブタスクの答えがわかっている場合にのみ真になるためです。私たちの場合、より短いサブセグメントの場合。したがって、最初にセグメントの長さをソートし、次に開始（または終了）する必要があります。

for ( int l = 2 ; l < n ; l ++ ) 
      

        
        
        
      

     for ( int a = 0 ; a + l < n ; a ++ ) { 
      

        
        
        
      

     int b = a + l ; 
      

        
        
        
      

     // ... 
      

        
        
        
      

     }

このサイクルでは、最後のツリーをソートして、削除の可能性を確認する必要があります。また、空の間隔のダイナミクスを初期化することを忘れないでください：

//       h2,      h1  h3 
      

        
        
        
      

     bool can ( int h1, int h2, int h3 ) { 
      

        
        
        
      

     if ( h1 < h2 && h3 < h2 ) return true ; 
      

        
        
        
      

     if ( h1 > h2 && h3 > h2 ) return true ; 
      

        
        
        
      

     return false ; 
      

        
        
        
      

     } 
      

        
        
        
      

     
      

        
        
        
      

     // ... 
      

        
        
        
      

     for ( int a = 0 ; a + 1 < n ; a ++ ) 
      

        
        
        
      

     del [ a ] [ a + 1 ] = a ; 
      

        
        
        
      

     
      

        
        
        
      

     for ( int l = 2 ; l < n ; l ++ ) 
      

        
        
        
      

     for ( int a = 0 ; a + l < n ; a ++ ) { 
      

        
        
        
      

     int b = a + l ; 
      

        
        
        
      

     for ( int i = a + 1 ; i < b ; i ++ ) 
      

        
        
        
      

     if ( del [ a ] [ i ] >= 0 && del [ i ] [ b ] >= 0 && can ( h [ a ] , h [ i ] , h [ b ] ) ) { 
      

        
        
        
      

     del [ a ] [ b ] = i ; 
      

        
        
        
      

     break ; 
      

        
        
        
      

     } 
      

        
        
        
      

     }

セカンドスピーカー

2番目のダイナミクスをint dyn [a] [b]とint fr [a] [b]の 2つの配列に保存します。最初は、実際には、サブセグメント（最小ツリーをいくつ削除する必要があるか）に対する答え、または非減少サブシーケンスを残すことができない場合は無限（10 ⁹を使用）です。そして、2番目の配列には、最初のリモートツリーに無限が書き込まれている場合は-1を格納し、最後のリモートツリーに格納します。

だから、私たちは書いています。ここで、途中ですべてを初期化できます（無限ループを埋める場合にのみ別のループが必要です）。

//     
      

        
        
        
      

     for ( int l = 1 ; l < n ; l ++ ) 
      

        
        
        
      

     for ( int a = 0 ; a + l < n ; a ++ ) { 
      

        
        
        
      

     int b = a + l ; 
      

        
        
        
      

     if ( h [ a ] > h [ b ] ) continue ; //     ,    
      

        
        
        
      

     if ( del [ a ] [ b ] >= 0 ) { //      ,   
      

        
        
        
      

     dyn [ a ] [ b ] = b - a - 1 ; 
      

        
        
        
      

     fr [ a ] [ b ] = a ; 
      

        
        
        
      

     } 
      

        
        
        
      

     
      

        
        
        
      

     for ( int i = a + 1 ; i < b ; i ++ ) { 
      

        
        
        
      

     //      ,   , 
      

        
        
        
      

     //      -      
      

        
        
        
      

     if ( h [ a ] > h [ i ] || h [ i ] > h [ b ] ) continue ; 
      

        
        
        
      

     
      

        
        
        
      

     //       ,    
      

        
        
        
      

     //   ,   
      

        
        
        
      

     int cans = dyn [ a ] [ i ] + dyn [ i ] [ b ] ; 
      

        
        
        
      

     if ( dyn [ a ] [ b ] > cans ) { 
      

        
        
        
      

     dyn [ a ] [ b ] = cans ; 
      

        
        
        
      

     fr [ a ] [ b ] = i ; 
      

        
        
        
      

     } 
      

        
        
        
      

     } 
      

        
        
        
      

     }

回答の回復

すでに上記で完全に記述されています-そのコードは完全に機能します。答えがあることを確認し、関数を呼び出し、結果を出力するだけです。

int a = 0 , b = n - 1 ; 
      

        
        
        
      

     if ( fr [ 0 ] [ n - 1 ] < 0 ) printf ( "-1 \n " ) ; 
      

        
        
        
      

     else { 
      

        
        
        
      

     ans = vector < int > ( ) ; 
      

        
        
        
      

     restoreAns ( a, b ) ; 
      

        
        
        
      

     printf ( "%d \n " , ans. size ( ) ) ; 
      

        
        
        
      

     for ( int i = 0 ; i < ans. size ( ) ; i ++ ) 
      

        
        
        
      

     printf ( "%d \n " , ans [ i ] + 1 ) ; 
      

        
        
        
      

     }

すべて一緒に

プログラム全体をpastebinで表示できます。彼女がオリンピックで書いたので、短縮ダイヤルの略語があり、コメントはありません。ただし、この記事では重要なコードをすべて引用しました。

テスト中

アルゴリズムの問題をテストするトピックについては、多くの大きな記事を書くことができます。しかし、私たちはすぐにしたいですよね？したがって、記事の冒頭でテストをダウンロードした場所を思い出し、どこかで解凍し（タスクはoaksと呼ばれます）、ペンで50のテストをすべて実行するか、 check.dprファイルをコンパイル（コンパイル）してCMDにスクリプトを記述します：

@echo off 
      

        
        
        
      

     for %% i IN ( tests\ ?? ) DO ( 
      

        
        
        
      

     del oaks. in oaks. out > nul 2 >& 1 
      

        
        
        
      

     copy %% i oaks. in > nul 2 >& 1 
      

        
        
        
      

     main > nul 2 >& 1 
      

        
        
        
      

     if errorlevel 1 exit 
      

        
        
        
      

     check oaks. in oaks. out %% i. a 
      

        
        
        
      

     if errorlevel 1 exit 
      

        
        
        
      

     ) 
      

        
        
        
      

     echo ALL IS OK ! 
      

        
        
        
      

     pause

始めます。碑文を見たら、 すべてが大丈夫です！ 「任意のキーを押す」-あなたの決定は正しいです。そうでない場合は、正しく動作しないテストがあります。このテストを急いで見ないでください-自分でバグを見つけて修正する方がはるかに便利です。

おわりに

伝えたかったのはそれだけです。あなたがすべてを理解し、あなたの時間を無駄にしないように願っています。

ご清聴ありがとうございました。

私は建設的な批判を喜んでいます。

サブセグメントダイナミクス：基本的なことと「1つが良いと2つが良い」

状態

主なアイデア

回答の回復

回答の回復

作業時間

書き方

最初のスピーカー

セカンドスピーカー

回答の回復

すべて一緒に

テスト中

おわりに

More articles: