データ構造：バイナリヒープ

バイナリヒープは、単純に実装されたデータ構造であり、要素をすばやく（対数時間で）追加し、最高の優先度（たとえば、最大値）を持つ要素を取得できます。



さらに読むには、 ツリーの概念が必要です 。また、アルゴリズムの複雑さの評価について知ることもお勧めします 。 この記事のアルゴリズムには、C＃コードが付随します。

はじめに

バイナリヒープは、ヒープのメインプロパティが満たされる完全なバイナリツリーです。各頂点の優先度は、その子孫の優先度よりも高くなっています。 最も単純な場合、各頂点の優先順位はその値と等しいと見なすことができます。 この場合、サブツリーのルートはサブツリーの要素の値の最大値であるため、構造はmax-heapと呼ばれます 。 この記事では、簡単にするためにそのような表現を使用しています。 各頂点に2つ以下の子孫しかなく、頂点レベルの充填が上から下に（同じレベルから左から右に）行われる場合、ツリーは完全なバイナリと呼ばれることを思い出してください。







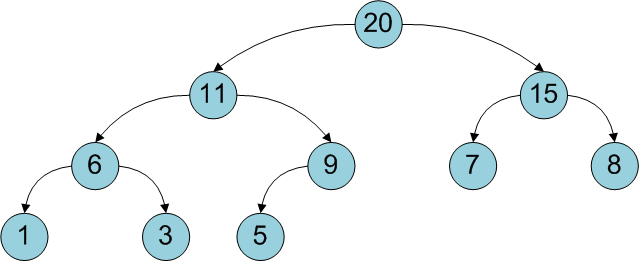
バイナリヒープを1次元配列の形式で保存すると便利です。インデックスi



の頂点の左の子孫はインデックス2*i+1



で、右の子孫は2*i+2



です。 ツリーのルートはインデックス0の要素です。バイナリヒープの高さはツリーの高さ、つまりlog ₂ Nに等しく、 N



は配列内の要素の数です。



C＃でクラスを空白にします：

 public class BinaryHeap { private List<int> list; public int heapSize { get { return this.list.Count(); } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

アイテムを追加

新しい要素は、配列の最後の場所、つまりheapSize



インデックスの位置にheapSize



ます。







新しい要素は親よりも大きいため、これがヒープのメインプロパティに違反する可能性があります。 この場合、ヒープのメインプロパティが観測されるまで、新しい要素を1レベル「親頂点で変更」する必要があります。











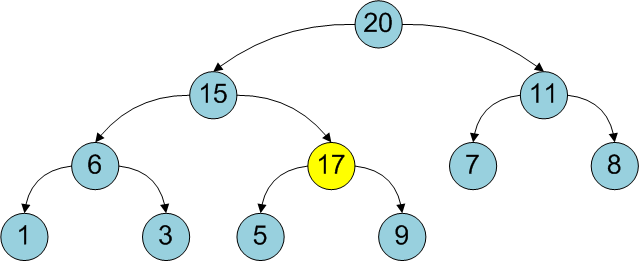
言い換えると、新しい要素は、それが配置されるまで「ポップアップ」し、「プッシュ」します。 アルゴリズムの複雑さはバイナリヒープの高さを超えない（「リフト」の数がツリーの高さより大きくないため）、つまりO（log ₂ N）に等しい。

 public void add(int value) { list.Add(value); int i = heapSize - 1; int parent = (i - 1) / 2; while (i > 0 && list[parent] < list[i]) { int temp = list[i]; list[i] = list[parent]; list[parent] = temp; i = parent; parent = (i - 1) / 2; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

バイナリヒープの順序

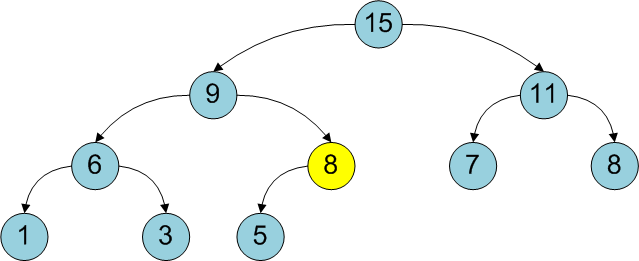
既に構築されたバイナリヒープを使用する他の操作の過程で、ヒープのメインプロパティも違反する可能性があります。頂点はその子孫よりも小さくなる可能性があります。







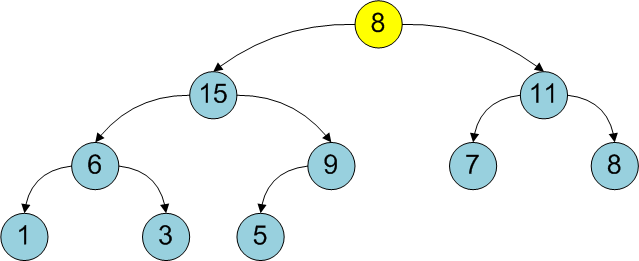
heapify



メソッドは、両方のサブツリーが満たす限り、i番目の頂点にルートを持つツリーの基本的なヒーププロパティを復元します。 このためには、メインプロパティが復元されるまで（最大の子孫との交換）、i番目の頂点を「下げる」必要があります（子孫がなく、その大きな親がなくなるとプロセスは終了します）。 このアルゴリズムの複雑さもO（log ₂ N）に等しいことがわかります。

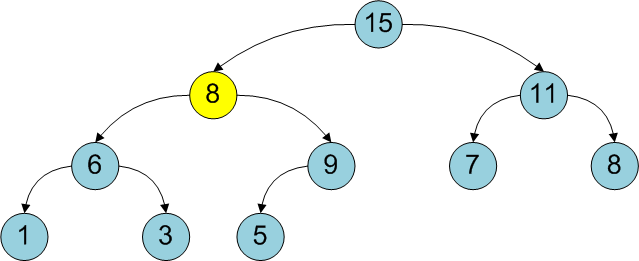
 public void heapify(int i) { int leftChild; int rightChild; int largestChild; for (; ; ) { leftChild = 2 * i + 1; rightChild = 2 * i + 2; largestChild = i; if (leftChild < heapSize && list[leftChild] > list[largestChild]) { largestChild = leftChild; } if (rightChild < heapSize && list[rightChild] > list[largestChild]) { largestChild = rightChild; } if (largestChild == i) { break; } int temp = list[i]; list[i] = list[largestChild]; list[largestChild] = temp; i = largestChild; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

バイナリヒープの構築

順序付けられていない配列から束を構築する最も明白な方法は、すべての要素を順番に追加することです。 このようなアルゴリズムの推定時間はO（N log ₂ N）です。 ただし、O（N）の場合は、さらに高速で束を作成できます。 まず、ヒープのメインプロパティを監視することなく、配列のすべての要素からツリーを構築する必要があります。次に、少なくとも1つの子孫を持つすべての頂点に対してheapify



メソッドを呼び出します（子孫のない1つの頂点で構成されるサブツリーが既に順序付けられているため）。 最初のheapSize/2



頂点には子孫があることが保証されています。

 public void buildHeap(int[] sourceArray) { list = sourceArray.ToList(); for (int i = heapSize / 2; i >= 0; i--) { heapify(i); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最大要素の抽出（削除）

順序付けされたmax-heap



最大要素は常にルートに格納されます。 最大の要素を削除した後にバイナリヒープの順序を復元するには、最後の要素をその場所にheapify



し、ルートに対してheapify



を呼び出します。つまり、ツリー全体を順序付けます。

 public int getMax() { int result = list[0]; list[0] = list[heapSize - 1]; list.RemoveAt(heapSize - 1); return result; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

バイナリヒープソート

最初にバイナリヒープを構築してから、最大要素を順番に抽出することで、配列をソートできることに注意してください。 そのような要素の時間の複雑さを評価しましょう：ヒープ構築-O（N）、 N



要素の抽出-O（N log ₂ N）。 したがって、最終スコアはO（N log ₂ N）です。 この場合、アレイ用の追加メモリは使用されません。

 public void heapSort(int[] array) { buildHeap(array); for (int i = array.Length - 1; i >= 0; i--) { array[i] = getMax(); heapify(0); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

おわりに

したがって、バイナリヒープは（頂点の数に対して）対数の高さのツリー構造を持ち、対数時間で要素を追加し、一定の時間で最大の優先順位を持つ要素を抽出できます。 同時に、バイナリヒープは簡単に実装でき、追加のメモリは必要ありません。