エントリー
昨年11月、「Pythonアルゴリズム:Python言語での基本アルゴリズムの習得」というタイトルのMagnus Lie Hetlandの本が登場しました。 著者は長年プログラミングに従事しており、現在、ノルウェーの大学の1つでアルゴリズムの理論のコースを教えています。 彼の本の中で、彼はアルゴリズムを構築し分析する方法をかなり簡単な言葉で説明し、Pythonプログラマー向けの多くの例を引用しています。 著者は、さまざまなアルゴリズムの問題に対するソリューションの構築と最適化への実用的なアプローチに焦点を当てています。 レビューの1つは、この本がCormenの古典的な作品と比較されることができると言います。
Tanannと私はこの本を少しずつ翻訳しています。この章の最初の部分である「アルゴリズムの経験的評価」の翻訳に注目してください。
アルゴリズムの経験的評価
この本では、アルゴリズムの設計(およびアルゴリズムの密接に関連する分析)について説明します。 しかし、実際の大規模なプロジェクトを作成する際に不可欠な、開発における別の重要なプロセスもあります;これはアルゴリズムの最適化です。 この分離の観点から、アルゴリズムの設計は、(効果的なアルゴリズムを開発することにより)アルゴリズムの漸近的複雑さを低くし、この漸近性に隠された定数の削減として最適化する方法と考えることができます。
Pythonの設計アルゴリズムに関するヒントを提供することはできますが、作業中の特定のタスク、またはPythonの機器とバージョンに対して、どのトリックとトリックが最高のパフォーマンスを提供するかを推測することは困難です。 (漸近線は、そのようなことに頼る必要がないように使用されます)。 一般に、プログラムは既に非常に高速であるため、場合によっては、トリックがまったく必要ない場合があります。 ほとんどの場合にできる最も簡単なことは、試してみることです。 ハックのアイデアをお持ちの場合は、試してみてください! トリックを実装して、いくつかのテストを実行します。 改善点はありますか? そして、この変更がコードの可読性を低下させ、パフォーマンスの向上が小さい場合、考えてみてください-それは価値がありますか?
いわゆる実験的アルゴリズムの理論的側面(つまり、アルゴリズムの実験的評価とその実装)は本書の範囲を超えていますが、非常に役立つ実用的なヒントをいくつか紹介します。
ヒント1.可能であれば、心配する必要はありません。
漸近的な複雑さを心配することは非常に役立ちます。 時々、実際の複雑さによる問題の解決は、そうではなくなるかもしれません。 ただし、漸近性の定数は、多くの場合まったく重要ではありません。 アルゴリズムを簡単に実装して開始し、安定して機能することを確認してください。 動作する場合は、触れないでください。
ヒント2. timeitを使用してランタイムを測定します。
timeitモジュールは、ランタイムを測定するように設計されています。 実際に信頼できるデータを取得するには多くの作業が必要ですが、実際にはtimeitで十分です。 例:
>>> import timeit >>> timeit.timeit("x = 2 + 2") 0.034976959228515625 >>> timeit.timeit("x = sum(range(10))") 0.92387008666992188
timeitモジュールは、たとえば次のようにコマンドラインから直接使用できます。
$ python -m timeit -s"import mymodule as m" "m.myfunction()"
timeitを使用する際には注意が必要なことがあります。timeitの再実行に影響する副作用です。 timeit関数は、コードを数回実行して精度を高めます。過去の開始が後続の開始に影響する場合は、困難な状況になります。 たとえば、mylist.sort()のようなものの実行速度を測定する場合、リストは初めてのみソートされます。 残りの数千回の起動中に、リストは既にソートされており、これは非現実的に小さな結果になります。
このモジュールの詳細と機能については、 Python標準ライブラリのドキュメントをご覧ください。
ヒント3.プロファイラーを使用して、ボトルネックを見つけます。
多くの場合、プログラムのどの部分に最適化が必要かを理解するために、さまざまな推測と仮定が行われます。 そのような仮定はしばしば誤りです。 推測する代わりに、プロファイラーを使用します。 Pythonには標準でいくつかのプロファイラーが付属していますが、cProfileをお勧めします。 timeitと同じくらい簡単に使用できますが、プログラムの実行時に無駄になった時間に関する詳細情報を提供します。 プログラムのメイン関数がメインと呼ばれる場合、次のようにプロファイラーを使用できます。
import cProfile cProfile.run('main()')
このようなコードは、さまざまなプログラム機能のランタイムに関するレポートを出力します。 システムにcProfileモジュールがない場合は、代わりにプロファイルを使用してください。 これらのモジュールの詳細については、ドキュメントをご覧ください。 実装の詳細にはあまり関心がなく、特定のデータセットでアルゴリズムの動作を評価する必要がある場合は、標準ライブラリのトレースモジュールを使用します。 式または呼び出しがプログラムで実行される回数を計算するために使用できます。
ヒント4.結果をグラフィカルに表示します。
可視化は、何が何であるかを理解するための優れた方法です。 パフォーマンス調査では、多くの場合、グラフが使用され(たとえば、データ量と実行時間の関係を評価するため)、複数の起動に費やされた時間の分布を示す箱ひげ図が使用されます。 図に例を示します。
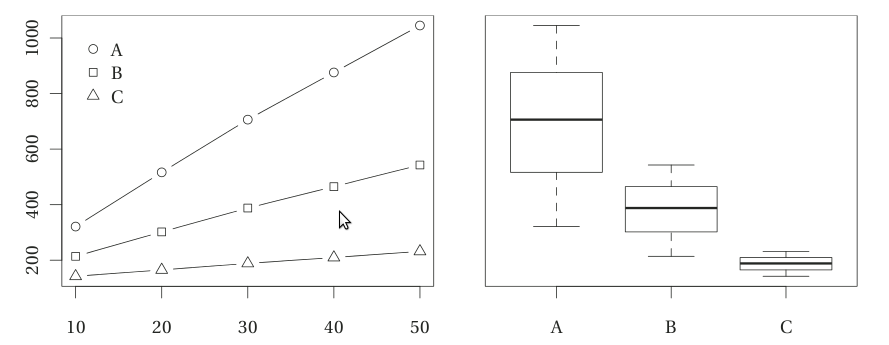
Pythonからグラフと図を作成するための優れたライブラリはmatplotlibです( http://matplotlib.sf.netで入手できます)。
ヒント5.実行時の比較に基づく結論に注意してください。
このアドバイスはかなりあいまいです。なぜなら、操作時間の比較に基づいて、どの方法が優れているかについて結論を導き出すことができる多くのトラップがあるからです。 まず、表示される違いは偶然に判断できます。 timeitのような特別なツールを使用する場合、式の計算時間の測定を数回繰り返します(または、最良の結果を選択して測定全体を数回繰り返します)ため、この状況のリスクは低くなります。 したがって、常にランダムエラーが発生し、2つの実装の差が特定のエラーを超えない場合、これらの実装が異なるとは言えません(同じであるという事実も述べられません)。
3つ以上の実装を比較すると、問題はさらに複雑になります。 比較するペアの数は、比較するバージョンの数の2乗に比例して増加し、少なくとも2つのバージョンがわずかに異なるように見える可能性が大幅に増加します。 (これは多重比較問題と呼ばれます)。 この問題には統計的な解決策がありますが、最も簡単な方法は、2つの疑わしいバージョンで実験を繰り返すことです。 これを数回行う必要があるかもしれません。 彼らはまだ似ていますか?
第二に、平均値を比較する際に注意する必要があるいくつかのポイントがあります。 少なくとも、リアルタイムの平均を比較する必要があります。 通常、パフォーマンスを測定するときに指数値を取得するために、各プログラムの実行時間は、標準的な単純なアルゴリズムの実行時間で割ることにより正規化されます。 実際、これは有用かもしれませんが、場合によっては、測定結果が無意味になります。 このトピックに関する有用なヒントは、Fleming and Wallaceの「統計に嘘をつかない方法:ベンチマーク結果をまとめる正しい方法」にあります。 また、Bast and Weberの「平均を比較しない」、またはCitronらの新しい記事「 調和平均または幾何平均:それは本当に重要ですか? 」も読むことができます 。
そして第三に、おそらくあなたの結論は一般化できない。 入力データの異なるセットおよび異なるハードウェアでの同様の測定では、異なる結果が得られる場合があります。 誰かがあなたの測定結果を使用する場合は、それらをどのように受け取ったかを一貫して文書化する必要があります。
ヒント6.実験の漸近的挙動について結論を出すときは注意してください。
アルゴリズムの漸近的振る舞いについて明確に言いたい場合は、この章で前述したように、それを分析する必要があります。 実験はヒントを与えるかもしれませんが、それらは明らかに有限データセットで行われ、漸近的な振る舞いはデータがarbitrarily意的に大きいときに起こることです。 一方、学術分野で働いていない場合、漸近解析の目標は、特定の方法で実装され、特定のデータセットで実行されるアルゴリズムの動作について結論を出すことです。つまり、測定は適切でなければなりません。
アルゴリズムは2次の複雑度で機能すると仮定しますが、最終的に証明することはできません。 仮定を証明するために実験を使用できますか? すでに述べたように、実験(およびアルゴリズムの最適化)は主に定数係数を扱いますが、解決策があります。 主な問題は、仮説が実際に実験的に検証できないことです。 アルゴリズムの複雑度がO(n²)であると主張する場合、データはそれを確認も拒否もできません。 ただし、仮説をより具体的にすると、検証可能になります。 たとえば、いくつかのデータに基づいて、環境内でプログラムの時間が0.24n²+ 0.1n + 0.03秒を超えないことを想定できます。 これは、検証可能な(より正確には、反論可能な)仮説です。 多くの測定を行ったが、反例を見つけることができない場合、仮説は正しいかもしれません。 そして、これはアルゴリズムの二次複雑性の仮説をすでに確認しています。
おわりに
本自体は、たとえばAmazonで注文できます 。
翻訳キューの次のものは、グラフとツリーの導入と操作に関する章です。 著者は、Pythonを使用してこれらのデータ構造を効果的に使用する実用的な側面について説明しています。