🏂🏼 💴 ⏏️ フラクタル風景を構築するためのダイヤモンド正方形アルゴリズム 🏠 👨🏽‍💻 📦

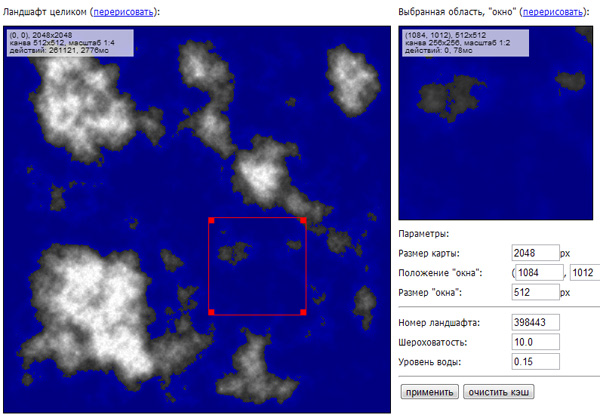
多くの人が非常に珍しいMinecraftゲームに精通していると思います（右はその中で生成されたマップの例です）。プレイヤーは地球の（ほぼ）無限の表面にいて、最小限の制限で彼の周りの世界を探索できます。

ゲームの作者であるノッチは、どのようにして彼のランダムな「世界」を地球の広大さに似せたものにしたのでしょうか？このトピックでは、この種の人工的なランドスケープを構築する方法の1つを検討し（また、他のいくつかの方法を簡単に説明します）、パフォーマンスを著しく低下させることなくランドスケープのサイズを大幅に増加できるこのアルゴリズムの小さな改善についても説明します

内部には、いくつかのスキームと美しい写真、かなりの数の文字、アルゴリズムの実装例へのリンクがあります。

行動計画

一般的にランドスケープ生成とはどういう意味ですか？実際にMinecraftなどのコンピューターゲームのレベルの作成（ほぼリアルタイム）について話す場合、このプロセスは次のポイントで構成されます。

高さマップを作成します 。最初に、平坦な2次元グリッドを作成し、各セルに特定の高さを割り当てます。どうやって？これについては後で説明します。ちなみに、グリッドは長方形である必要はありません。たとえば、三角形で構成されるグリッドの同様のアルゴリズムをここで説明します。ただし、ほとんどの場合、正方形のピクセルセルで構成されるグリッドの方が便利です。高さマップとともに、水で覆われたエリアも定義されます-少なくとも海と海（通常、特定のレベルより下にあるセルは水になります）。
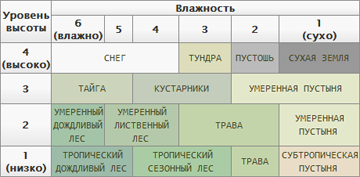バイオーム分布 。ここでは、地理の知識が必要になります（ただし、ランドスケープを作成するプロセス全体でこれが必要です）。ツンドラがどこにあるべきか、砂漠がどこにあるか、そして熱帯雨林がどこにあるかを決定するために、すでに作成された高さマップと、例えば、水空間またはいくつかの所定のポイント（赤道/極）までの距離が役立ちます。次に、バイオームは他の多くのパラメーターを設定します-例えば、草地、岩場の数、植物、川や湖の数など。
地球、海洋、海も作成し、地理的ゾーンを分散させました。何を忘れましたか？もちろん、川をしましょう ！山から流れて海に流れ込む、または空洞に湖を形成する水自体に加えて、地表面への影響をエミュレートする必要があります-川底が形成され、砂や柔らかい土壌が河川に沿って運ばれ、湖や他の水域のビーチが形成されます。残念ながら、他のタイプの侵食と同様に、 水侵食と呼ばれるこのプロセスは、この記事の範囲外にする必要があります。それでも、参考文献のリストには、このトピックに関する非常に優れた資料へのリンクがいくつかあります。
追加のアクション 。実際、景観はすでに作成されていますが、改善できるものはまだ多くあります。たとえば、Minecraftでは、地下空間が完全に自然の洞窟で覆われ、多くの樹木が表面に生えています。さらに、もちろん、バイオームによっては、動植物を多様化することが可能です-目標が現実に起きていることにできるだけ近づくことである場合。

最後に、生成されたランドスケープを描画するだけで済みます。ここで詳細を1つだけ確認します。上記の三角形のグリッドは、3次元マップの従来の視覚化の場合に役立ちますが、ボクセルの使用は正方形のセルには非常に役立ちます。ただし、これはまったく別の話です。

高さマップを作成する方法

それでは、ランドスケープを構築する上で最も重要な段階を見てみましょう。地表の各ポイントの高さを決定します。最も一般的なアイデアは、両方の座標を調べてマップ[x] [y] =ランダム（）にすることです。奇妙なことに、許容できる結果が得られないため、もっとsomethingなものを使用する必要があります。

「手動で」丘を作成する

かなり単純なアルゴリズム：最初から、すべてのポイントは同じレベルにあり、任意の場所（高さの異なる丘）に何らかの「バルジ」を追加し始めると考えています。慎重にこれらの丘を互いの上に敷設した結果（および、上記の少しのノイズが追加された可能性があります）、すでに真実に似たものを得ることができます。ただし、以下にリストしたアルゴリズムを使用すると、はるかに現実的なランドスケープを実現できます。そのため、「丘」方式については説明しません。

ボロノイ図に基づく風景

実際、最近まで、次のアプローチは私にはまったく知られていませんでしたが、非常に印象的な結果を出すことができたことに非常に驚きました。

それはすべて、誤ってマップ上にポイントを投げることから始まります。次に、これらの点からボロノイ図（および、それに応じてDelaunay三角形分割）が構築され、ロイドの緩和のいくつかの反復が実行されて、小さすぎるポリゴンが削除されます。

前の段落が明確でない場合-怖くない、その本質は右の図のようなグリッドについて作成することになります。その主な特性は不規則性です。これにより、基礎に基づいて構築されたランドスケープが「正方形」に見えすぎないようにできます。

それ以上のアクションは簡単です。水で満たすポリゴンをランダムに選択し、残りのポリゴンに属するポイントの高さをsea-okiyanaまでの最短距離に等しくします。同じノイズ（高度自体とポリゴンの境界の両方）を追加するために残ります-そして、非常に素晴らしい島（または規模に応じて本土）を取得します。

私はこのアルゴリズムの実装を扱っていませんでした。そして、記事を簡単にするために、いくつかの詳細と中間のものを省略しました。詳細な記事（写真とほとんどの情報の出典）はここ（英語）にあります。また、プロセスのすべての段階を非常に明確に示す素晴らしいswfデモもあります。

ダイアモンドスクエアアルゴリズム

最も一般的で最も現実的な結果をもたらすのは、1次元中点変位アルゴリズムを2次元平面に拡張したダイアモンドスクエア（またはスクエアダイアモンド）アルゴリズムです。その助けを借りて得られた風景は、原則としてフラクタルと呼ばれますが、確かに、実際にはそれほど自己類似ではありません-反対に、以下で見るように、あまり快適ではない特性は、大規模に比較的滑らかになることです、小さなものは一種のサンドペーパーに変わります。

真夜中の変位夜の地平線

より単純な中点変位アルゴリズムから始めましょう。既に述べたように、2次元の平面ではなく、1次元のセグメント上で機能します（したがって、たとえば、それを使用して水平線を作成できます）。

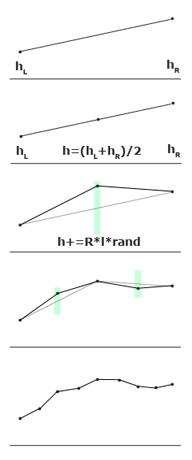
このアルゴリズムがフラクタルに関連しているという事実は、その再帰的な動作です。最初に、セグメントの両端の高さを何らかの方法で設定し、中央のポイントで2つのサブセグメントに分割します。このポイントをランダムな値でシフトし、取得したサブセグメントごとにパーティションとシフトを繰り返します。など-セグメントの長さが1ピクセルになるまで。これがアルゴリズム全体です（右の図を参照）。ああ、はい-重要な注意：ランダムな変位は、パーティションが作成されるセグメントの長さに比例する必要があります。たとえば、長さlのセグメントを分割します-中央のポイントは高さを持つ必要があります

h =（ h _L + h _R ）/ 2 +ランダム（ -R * l 、 R * l ）

（ h _Lとh _Rはセグメントの左端と右端の高さで、定数Rは結果のポリラインの「粗さ」を決定し、このアルゴリズムの主要なパラメーターです）。

二次元の中点変位

このアルゴリズムを2次元の高さマップに一般化してみましょう。まず、マップ全体の4つの角にランダムな高さを割り当て、それを（便宜上、正方形のマップで作業し、その辺は2のべき乗であると仮定して）4つの等しい正方形に分割します。それらのそれぞれで、角度の1つの意味が知られています。残りはどこで入手できますか？二次元の中点変位の結果

1次元の中点変位の場合と同様に、すべて同じ補間-中心の点は、4つのコーナー点すべての高さを平均して得られ、大きな正方形の側面の各中点は、対応する辺の端にある1組の点を平均します。（正方形の辺に比例する範囲内で）中心点をランダムに上下にシフトするために、少しノイズを導入し、結果のサブ正方形に対して再帰的にアクションを繰り返すことができます。それだけですか？これですべてですが、すべてではありません。

これはまだダイアモンドスクエアではありません-このアルゴリズムは、原則として、中点変位アルゴリズムとも呼ばれます。比較的許容できる結果が得られるという事実にもかかわらず、結果の画像でその「まっすぐな」性質に簡単に気付くことができます。

ダイアモンドスクエアアルゴリズムの進捗

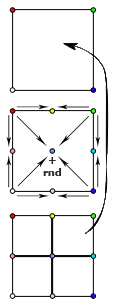
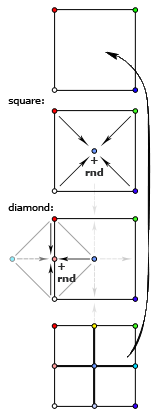ダイアモンドスクエアアルゴリズム（「実際の」フラクタルランドスケープを取得できるアルゴリズム）は、2つのステップで構成されるという点で2次元の中点変位とは異なります。最初は、いわゆるです。「Square」-同様に、角度を平均し、実際の変位を加算することにより、正方形の中心点を決定します 'a-ランダム偏差。 2番目のステップ「ダイヤモンド」は、辺の中央にあるポイントの高さを決定するように設計されています。ここでは、2つのポイント、つまり「上」と「下」（垂直側のポイントについて説明します）ではなく、「左」と「右」のポイントのペア、つまり「正方形」のステップで得られた2つの中心点を平均します。前のステップで取得したこれらの2つの高さはすでにカウントされていることに注意することが重要です。したがって、計算は「レイヤー」で実行し、最初にすべての正方形に対して「正方形」ステップを実行し、次にすべての菱形に対して「ダイヤモンド」ステップを実行し、より小さな正方形に。

説明はわかりにくいかもしれませんので、添付のスキームを注意深く検討することをお勧めします。各スキームでポイントの高さがどのように計算されるか、より明確にする必要があります。

深さを歩くのではなく幅を歩く必要があることに加えて、別の微妙な点があります-風景の端の状況です。実際、ダイヤモンドの段階では、アルゴリズムは現在の正方形の外側にあるポイントの高さを使用し、場合によってはマップ全体を使用します。になる方法 2つのオプションがあります（もちろん、独自に考え出すこともできます）：これらの高さを0（または1、または他の定数。これは、私たちの風景の端を水に浸すのに便利です）に等しいか、飛行機が折り畳まれていると想像してくださいトーラス（トロイダル惑星、うーん...）とマップの左境界線の左に64ピクセルある点の高さを見つけようとすると、右境界線から64ポイント離れた点の高さを見つけます。それは非常に簡単に実装されます（ただし、最初のオプションとして）-マップのサイズに等しいモジュロ座標を取ることで助けられます。

ダイアモンドスクエアアルゴリズムの結果

したがって、これらは、人工的に生成された景観の高度マップを構築するための基本的なアルゴリズムです。私の意見では、最も現実的な結果はそれらの最後のダイアモンドスクエアによって与えられます-それはいくつかの欠点がないわけではありませんが。たとえば、強力な近似で見栄えの良いマップを作成することで、全体を表示すると、いくつかの大きな大陸や海の代わりに、多くの小さな島（または開始時のノイズ）が表示されます。自己相似性は出てきません。これは、異なるスケールのフラクタルランドスケープのさまざまな組み合わせによって修正できます。それらの値は、乗算、加算、さまざまな係数での使用、または、たとえば、ボロノイ図を使用して取得したデータを取り込むことができます。一般に、実験の範囲は十分に広いです。ところで、1つのダイアモンドスクエアのみを使用しても、取得した値（以前は正規化された、つまり0.0から1.0の範囲）を二乗すると便利です。これにより、平野がより穏やかになり、山の傾斜が急になります（浸食について覚えていますか？）。

大きな地図用の菱形アルゴリズムの修正

最後に、ダイアモンドスクエアアルゴリズムの実装について少し説明します。ランドスケープを生成するときに尋ねる主な質問は、そのサイズを大幅に増加させる方法です。説明したアルゴリズムの標準実装により、詳細（「深さ」に移動）を簡単に増やすことができますが、次元（「幅」）にはできません。

私はこの問題を次のように解決しました。わからない-おそらく、この決定は誰かによく知られているか、非常に明白であることが判明するかもしれませんが、その前に私はそれに気付かず、すぐに思い付きませんでしたそして失敗しました-その下の詳細）。

そのため、アプローチは次のようになります。私たちのランドスケープは、もともと巨大なサイズ（たとえば、16777216x16777216ピクセルですが、これは限界からはほど遠い）で構想されています。重要なことは、 各ポイントの高さを調べるのではなく、かなり小さな「ウィンドウ」（たとえば、128x128ピクセル）を取得し、高さマップ上を移動する必要があることです。元のアルゴリズムは簡単に変更できるため、ウィンドウのサイズに比例する操作の数である「ウィンドウ」を計算する必要がありますが、ランドスケープのサイズにはほとんど依存しません。そのため、最初はランドスケープをほぼ任意に大きく設定できます。

レイジーダイナミクスと呼ばれる手法が役立ちます。私が話していることを知っている人にとっては、私が説明する問題を知らない人にとっては、すでに明らかになっていると思います。プロセス全体を裏返します-大きな正方形から始めて各ピクセルに行く代わりに、「ポイント（x、y）で高さを見つける」という形式のリクエストを受け入れ、上に移動します。他の4つのポイントとランダムシフトを平均することで得られました。最も難しいのは、これらの4つのポイントが何であったかを理解することです。これを理解した後、「高さを調べる」というリクエストを繰り返すだけで十分ですが、これらのポイントのそれぞれについてです。これらのリクエストは、順番に1レベル高くなり、最上部に到達してマップのコーナーポイントに達するまで続きます（私にとっては、マップの外側のポイントと同様に、0.0に等しい）。ソースでは、すべて次のようになります。

function val(x, y, v) { if (typeof(v) != 'undefined') data[x + '_' + y] = Math.max(0.0, Math.min(1.0, v)); else { if (x <= 0 || x >= size || y <= 0 || y >= size) return 0.0; if (data[x + '_' + y] == null) { //       . base = 1; while (((x & base) == 0) && ((y & base) == 0)) base <<= 1; if (((x & base) != 0) && ((y & base) != 0)) squareStep(x, y, base); else diamondStep(x, y, base); } return data[x + '_' + y]; } } function displace(v, blockSize, x, y) { return (v + (randFromPair(x, y, seed) - 0.5) * blockSize * 2 / size * roughness); } function squareStep(x, y, blockSize) { if (data[x + '_' + y] == null) { val(x, y, displace((val(x - blockSize, y - blockSize) + val(x + blockSize, y - blockSize) + val(x - blockSize, y + blockSize) + val(x + blockSize, y + blockSize)) / 4, blockSize, x, y)); } } function diamondStep(x, y, blockSize) { if (data[x + '_' + y] == null) { val(x, y, displace((val(x - blockSize, y) + val(x + blockSize, y) + val(x, y - blockSize) + val(x, y + blockSize)) / 4, blockSize, x, y)); } }

主なことは、すでに計算したすべての高度値を記憶（およびキャッシュに追加）することです。これにより、同じことを何度も行うことができなくなります。実際、「ウィンドウ」の最初のポイントを計算したとしても、この「ウィンドウ」に属する他の多くのポイントを同時に認識します。実際、「ウィンドウ」のすべてのポイントを実行したので、不必要な操作はあまり行いません。ただし、その正確な数は、「ウィンドウ」（左上隅とサイズ）が2のべき乗で整列しているかどうかに大きく依存します。

既に述べたように、アルゴリズムにはいくつかの魔法の行があります-ここにあります：

 base = 1; while (((x & base) == 0) && ((y & base) == 0)) base <<= 1; if (((x & base) != 0) && ((y & base) != 0)) squareStep(x, y, base); else diamondStep(x, y, base);

ここでは、現在の点が正方形または菱形の中心であるかどうか、およびこの図形のサイズは何かを決定します。正直に言うと、このコードは直感によって書かれたものであり、正確な数学的正当性を示すことはできません。少なくともいずれかの座標でゼロ以外の最下位ビットを見つけるだけです-望ましいサイズになります。そして、図が正方形かどうかを判断するために、このビットが両方の座標に設定されていることを確認します。ここでは、両方の座標にnullインデックスが付けられています。

そして最後に、予想外の落とし穴：擬似乱数ジェネレーター。私のコードでは、異常な要件が課されていました。各ポイント（x、y）に対して、常に同じ乱数を取得したいので、すぐにそれを行います。乱数ジェネレーターの多くのプログラミング言語には、いわゆる生成された数値の次のシーケンス全体が依存する「シード」（JavaScriptではこれは異なりますが、彼には広範囲にわたるMersenne vortexの実装があります）。問題は、シーケンスが私たちに合わないということです-ウィンドウをシフト（およびキャッシュをクリア）すると、完全に異なる側の1つのポイントに近づき、ランダムシフトが異なります。どんな状況でも、それを考慮して、静的な景観が必要です。両方の座標に応じて「粒子」で毎回メルセンヌ渦を初期化する試みは失敗しました：初期化に時間がかかりすぎます。

少し考えてから、2つの座標をそれらにほとんど相関しない数に変換する簡単な方法は、原則として不可能であるという結論に達しました。その結果、単純なモジュールによる複数の数字の取得により、許容可能な結果が得られるような関数に決めました。

 function randFromPair(x, y) { for (var i = 0; i < 80; i++) { var xm7 = x % 7; var xm13 = x % 13; var xm1301081 = x % 1301081; var ym8461 = y % 8461; var ym105467 = y % 105467; var ym105943 = y % 105943; y = x + seed; x += (xm7 + xm13 + xm1301081 + ym8461 + ym105467 + ym105943); } return (xm7 + xm13 + xm1301081 + ym8461 + ym105467 + ym105943) / 1520972.0; }

さらに、この関数に「グローバルグレイン」を簡単に導入することができました。これは、ランドスケープ全体を決定し、残基の取得により、その戻り値は[0、1）の範囲にかなり均等に分布することが判明しました。しかし、私はあなたがより速くエレガントなソリューションを思いつくことができると確信しています-この記事でこの「宿題」を考慮することができます:)

おそらく誰もが推測したように、JavaScriptで実装を作成したため、値とソースコードの両方を簡単に試すことができます。ページ自体はhttp://denull.ru/terrain.htmで入手でき、すべてのコードはファイルhttp://denull.ru/terrain.jsにあります。表示するには、html5をサポートするブラウザーが必要です（正直なところ、Google Chromeでのみテストしました）。これは、レンダリングがキャンバスに送られるためです（また、レンダリング自体にも時間がかかります）。

フラクタル風景を構築するためのダイヤモンド正方形アルゴリズム