アクション空間に3つ以上の空間次元が含まれるゲームを作成するときに発生する問題の1つは、アクションシーンの視覚化です。これは、ユーザーが十分に理解でき、ゲームのキャラクター(またはオブジェクト)と画像を作成する仮想カメラの両方を制御するのに適しています。
最近出会った多次元ゲームのほとんどはパズルでした-ルービックキューブの類似物。 しかし、パズルのさまざまな次元について、著者はさまざまな視覚化方法を使用する必要がありました。
ルービックキューブの4次元アナログ
これらのゲームでは、作業オブジェクトは凸型の4次元多面体であり、ほとんどの場合、高度の対称性(たとえば、等辺)を持っています。 最初は、各面は独自の色でペイントされますが、面が回転すると、色が混合されます。 目標は、元の色の順序を復元することです。
多面体のすべての頂点は、4次元の球上にあります。 視覚化のために、このグリッド(頂点のセット)の3次元空間へのステレオ投影が行われ、3次元多面体がその中に構築されます-元の立方体の面の投影。 顔は小さな多面体(「ステッカー」-通常の立方体の小さな正方形の類似物)に分割され、わずかに小さいサイズになっています(内部ステッカーがある場合は、それを見ることができます)。 結果のモデルは、モデルの中心に常に向けられたカメラで3Dビューアーに表示されます。 tesseractの特定のケースでは、7つの顔が表示されます。これはゲームに十分です。 カメラの焦点距離(視野角)とカメラから中心までの距離を制御できます。

5次元ルービックキューブ
視覚化もほぼ同じ方法で行われますが、ステレオ投影は4次元空間になります。 さらに、3次元に前向きに投影されます。 4次元のステッカーはrib骨モデルとして描かれており、of骨の色は元のステッカーの色に対応しています。

七次元の立方体
4つの「メイン」測定値と3つの「追加」測定値が選択されます。 主な次元で7つの面を考えます。それぞれが6次元の立方体です。 この立方体はフラクタルの方法で表されます。主な測定値に従ってN ^ 3個の立方体に分割され、各立方体は追加の次元のN ^ 3個のステッカーで構成されます。
主面は、ステレオ投影の4次元立方体の面と同じ方法で配置されます。
顔の少なくとも一部を追加の寸法で表示するために、ステッカーが考慮されます。 「メイン」面に隣接し、各面の小さな立方体の表面に配置されます(したがって、それらはN ^ 3ではなく(N + 2)^ 3であることが判明します)。
結局のところ、このような7次元の立方体を組み立てることは非常に可能です。

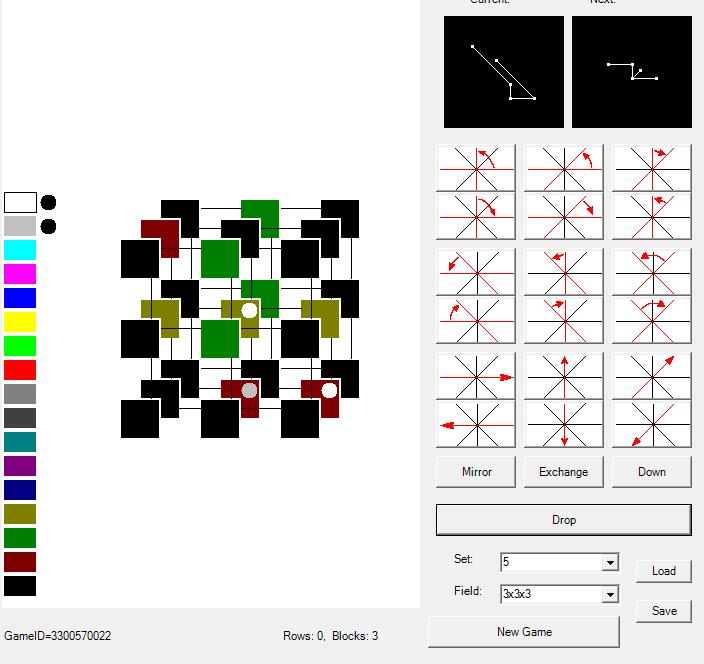
四次元テトリス
3次元ビューアも使用しません。投影はすぐに2Dになります。 ガラスを上から見ると、直方体が見え、その各セルはそれぞれの高さまで満たされています。 セルは標準的な方法(セルの斜めのチェーンで構成される長方形)で描かれ、高さは色分けされています。 落下する図形は、最初にそのワイヤフレームモデルで、次に影で(セルの一部に影が付けられます)、次にガラスの垂直投影で(色の順序と図の位置が見える)に表されます。
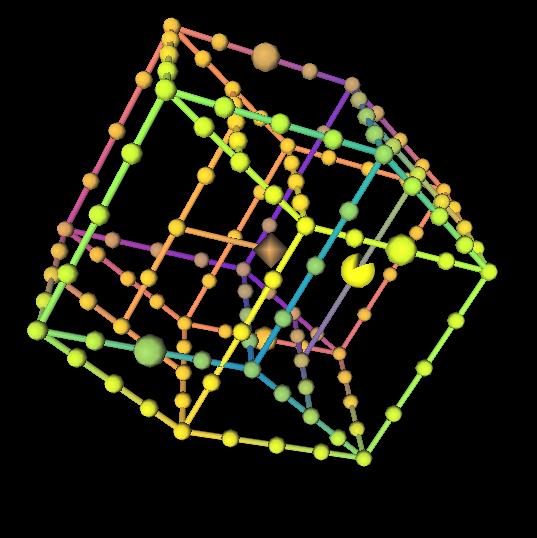
> 5次元のパックマン
ワイヤフレーム迷路モデルが使用されます(歩き回れるセグメント)。 モデルは3次元空間に投影されます(追加の座標は色で表示されます-Uは黄紫軸、Vは赤青軸)。 迷路は3Dビューアに表示されます。 3D(右/左および上/下)および色空間(黄色、紫、青など)の両方でカメラを回転させることができます(パックマンを制御する役割も果たします)。 これらのターンはモデルのスキューのように見えます。頂点の一部が近づいている、一部が削除されている、迷路の一部が色を変えています。
ロバチェフスキー空間のパズル
視覚化には、通常の3Dビューアが使用され、カメラは空間内にあり、光線は直線に沿って伝播します(ロバチェフスキー空間の測地線)。 カメラセンサーはほぼ平らです。

「三次元網膜」
別の視覚化方法があります( BlockBuildingゲームで使用されます) -3次元網膜での正直なビジョン:最初にカメラが見るものを計算し(これは色付きの3次元空間です)、次に2Dに投影されます。 これはおそらく、線分または半透明の2D面としてレンダリングする場合にのみ意味があります。