MDとは?
ウィキペディアが言うように、MDは相互作用する原子または粒子のシステムの時間的進化を、それらの運動方程式を統合することによって追跡する方法です。
さらに簡単な場合は、初期条件(速度、粒子の位置、粒子の種類)を設定し、相互作用の法則を知って、その結果を調べます。 古き良きライブゲームを思い出します。
数学
ここではすべてが非常に簡単です。 粒子(私の特定の場合、原子)間の相互作用は、古典的な物理学を使用して計算されます。

この一見紛らわしい式は、実際には学校F = maの完全な類似物です。
(実際、「混乱した」フォーミュラはより長く、見た目があまり美しくありません-消散成分を意図的に忘れていました)
数学的には、粒子シミュレーションは上記の方程式のコーシー問題の解決策です。
このすべてを計算するために、Verletアルゴリズムを委任しました。
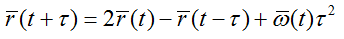
私見、それは精度と速度が最適です。 一つのこと-彼は粒子の以前の2つの位置を知る必要があります! したがって、最初のステップはオイラーを不正確にするために残されています。
どこにもポテンシャルがない
上記の式の(r)は、ポテンシャルによって決定されます。 一般的に、ここでの可能性は王と神です。最も重要なのはまさに彼の影響です。 私は非常に人気のあるものを選びました-レナード・ジョーンズに会います:
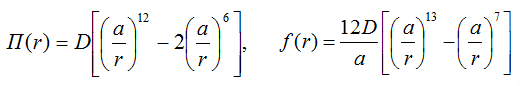
そして、これは見た目です。ここでは原子間距離、 fは相互作用の力、 rは粒子間の距離です。
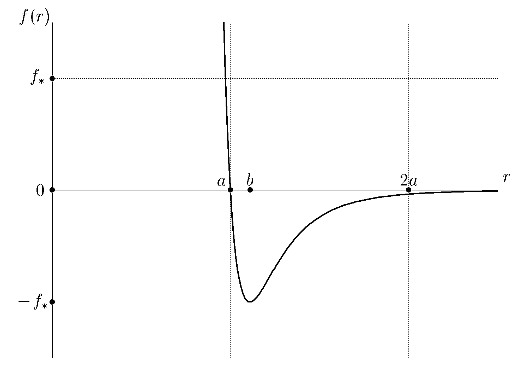
十分な数式
プログラミングに移りましょう。 これをすべてコードに記録すると、出力で加速度と座標の配列を取得します(ああ、はい、Verleは速度で動作しません。たとえば、中央の差を使用して速度を取得できます)。 このような詰め物の視覚化は、特に煩わしいことではなく、OpenGLに指示しました。
破片を見てみましょう(1083個の粒子、ストライカーがターゲットに「落ちる」)





それはまさにこの瞬間であり、おそらく最も楽しいものです-新鮮なモデルで遊ぶこと。 計算速度が低下しただけで、最適化の時が来ました。
スピードアップ
まず、物理学に戻らなければなりませんでした。 可能性を一度見ただけでそれが明らかになりました-半径が2aより大きい-数えられません。 つまり 最も簡単な方法は、各パーティクルが、想定するパーティクルの中心を持つ半径a2の球に落ちるパーティクルとの相互作用のみを考慮することです。 1つの条件は「if」であり、計算は数回加速されます(粒子と領域の数に応じて)。
私の病院で1つのコアの負荷をすべて見るのは退屈な作業です。 プロセスを並列化する時が来ました。 特にmdは完全に並列であるため。 それは単純に思えます-対応を設定します:粒子はプロセッサとカウントです。 実践が示しています-並列化する方が良いでしょう、スペースをグリッドに分割するのはそのためです。
セルサイズがaのグリッドを作成することで、1石で2羽の鳥を殺します-相互作用が考慮される計算領域の問題を解決し、プロセッサー間の交換をより透明でシンプルにします。 2つのプロセッサの例では、次のようになります。

ここでは、初期状態に応じて、どのモデルもさまざまな「ハッキング」によって「追跡」されることに言及する価値があります。 たとえば、無限(または巨大)なものをモデル化する必要があり、同時に1つまたは複数の方向で同じ構造を持つ場合、周期的な境界条件を適用できます。 これを使用して、2つの無限の表面の摩擦をシミュレートしました。
ここでのポイントは、その計算ドメインの周りに、粒子の実際の位置とともに「画像」が構築されるということです。 そして、「実」領域の粒子は、「画像」内の粒子と相互作用します。 そして、粒子が計算領域の境界を越えると、反対側に現れます(別名pacmanのトンネル)。 以下は、xとyの周期条件の例です。
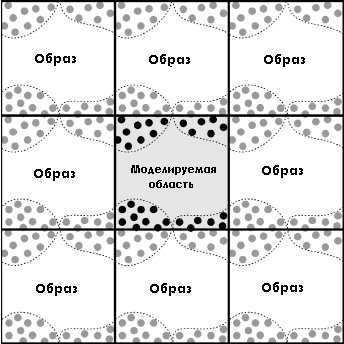
しかし、摩擦をシミュレートするために、私は1つの軸だけで定期刊行物を使用しました。




おわりに
かなり興味深く直感的なモデルであることが判明しました。実際の計算に使用したり試してみたりすることは非常に可能です(結果の信頼性は非常にまともです)。 適切なアプリケーションの場合、CudaまたはOpenCLの下でシャープにする価値があります。適切な並列化を使用してビデオカードのMDを計算する速度は、非常に高いです。 しかし、あなたの怠beに賭けて-すぐにこれは起こりそうにありません。
PS:ほとんどの場合、 粒子法と変形可能なソリッドケースの力学での使用という 1本だけに依存していました。 Krivtsov A.M.、Krivtsova N.V.