TAUダーウィニズム：Rubyの実装

まえがき

聞いて、カラス、多分犬、 牛かもしれませんが、それでもいいです！ 羽があり、角があります ひづめは非常に細長く親切です。

漫画「プラスチックカラス。」



この記事では、動的システムの識別に対する進化的アプローチの実装に注目します。 プログラムは、Rubyバージョン1.9.2（gems：NArray、GNUPlot）で記述されています。 猫の下を見ると、遺伝子情報のマテリアルコーディングの例とそれに適した「フラットクロスオーバー」アルゴリズムがあります。

はじめに

ブラックボックスタスクの説明から始めます。 伝達関数を知りたい特定のオブジェクトがあると仮定します（簡略化された、近い、または本物と同等）。 できることは、オブジェクトの入力に何らかの影響を与え、出力パラメーター（出力電圧など）を測定することだけです。 箱の中身をどうやって見ることができますか？ 言い換えれば、研究対象の近似数学モデルを決定する方法は？

自動制御理論（TAU）では、この問題は識別と呼ばれます。 真剣な数学に基づいたさまざまな識別方法があり、実装が困難です。 ただし、比較的簡単な方法で、つまり進化アルゴリズムを使用した確率的アプローチを使用して、近似数学モデルを取得することは可能です。

この問題に関する最初の記事TAU-Darwinismで詳細を読むことができます。ここでは、ソフトウェアの実装に焦点を当てます。

実装

アルゴリズムを記述するとき、ライブラリ「gga4r」（rubygems.org）を使用しました。 このライブラリは、ruby 1.9との互換性のために動作するように書き直されました 。 このライブラリの作成者（ありがとうございました！）内容の違いはあるが形は同じで、進化する個人の表現を実現するエンティティに対して、進化的ラッパーアプローチを実装しました。 遺伝演算子を実装する独自のクラスを実装することが提案されています。 私はこのようになった：

class TFIndivid attr_reader :filter, :fitness, :dna, :num_len, :denom_len def initialize(num,denom,k=1.0,ts=@@ts) @num_len,@denom_len,@filter = num.length,denom.length,SSF::tf2ssd(num, denom, k, ts) @fitness = 1/(step_response_deviation(@filter)+@@eps) @fitness = 0.0 if @fitness.infinite? @dna = num + denom + [k] + [ts] self end def integrity_ok?(dna) return dna.length == @num_len + @denom_len + 2 end def TFIndivid.flat_crossover(par1, par2) r = Random.new child = [] par1.size.times { |i| if par1[i]>par2[i] child << r.rand(par2[i]..par1[i]) else child << r.rand(par1[i]..par2[i]) end } child end def recombine(other) child = TFIndivid::flat_crossover(self.dna, other.dna) res = self.integrity_ok?(child) ? TFIndivid.new(child[0..@num_len-1], child[@num_len..-3], child[-2], child[-1]) : [] [res] end def mutate rnd = Random.new mutate_point = rnd.rand(@dna.size-1) @dna[mutate_point] *= rnd.rand(1.0) end end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

gga4r Webサイトの例では、個々のクラスが配列から継承されています。 ロジックを少し変更することにし、追加のプロパティ「@dna」を取得しました。 これは、コンストラクターの利便性と使用のために行われました。コンストラクターでは、伝達関数のゲイン、分子、分母のデータ（連続時間）、および時間量子化期間に対してデジタルフィルターが作成されます。 また、コンストラクターでは、転送されたパラメーターが1つの1次元配列にマージされ、遺伝的アルゴリズムを使用してパラメーターが処理されます。 フィットネスの個人は、コンストラクターですぐに計算され、対応するプロパティに保存されます。

「flat_crossover」関数は、記事の冒頭で述べたマテリアルの交差を実装します。 これはおそらく最も簡単な実装です。 さらにいくつかの子が実現され（ここでは1つの子孫が生成されます）、おそらく実現する必要があります。 この場合、生成された子は、親の遺伝子の値の間の間隔で各遺伝子の乱数を選択することにより形成されます。

突然変異演算子は、遺伝子値に[0.0..1.0]の範囲の乱数を乗算することで実装されます。 したがって、一部の遺伝子はゼロに「引き付けられ」ます。 選択された交叉演算子は、主に値の許容範囲の中央にある遺伝子値を持つ個体を形成します。 選択された突然変異方法は、カウンターウェイトの役割を果たします。

進化的アルゴリズムのラッパー自体は、以前のTAU-Darwinismの記事で説明されているように機能します。集団が形成され、選択、再結合（交差）、突然変異が実行されます。 プログラムのソースコードで内部を見ることができます（記事の最後のリンク）。 上記のように、ruby 1.9で使用できるように、少し書き直さなければなりませんでした。 しかし実際、ライブラリはkubuntu 10.10のバージョン1.8での動作を拒否しました（理由はわかりませんでした）。 可能であれば、元の「gga4r」と比較できます-変更点はほとんどありません。 変更する他の何か。

適合度関数は、テストフィルターの出力信号と遺伝子によって生成された個体の間の標準偏差として実装されます。

 def step_response_deviation(filter) x, test_y,y = step_response(filter) av_err = 0.0 100.times {|i| err = test_y[i] - y[i] av_err += err*err } Math.sqrt(av_err / 99) end def step_response(filter) @@test_filter.reset filter.reset x = []; 100.times { |i| x << i*@@ts } test_y,y = [],[] 100.times { test_y << @@test_filter.step(@@test_input) y << filter.step(@@test_input) } return x,test_y,y end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは問題のステートメント（「ブラックボックスの出力と入力の記録が必要です。必須です...」）とは少し異なりますが、より便利ですが、本質は同じです。

結果

新しい小さなタグで遊ぶ予備調査の間に、より少ない反復で大きな母集団サイズを設定することが最も有益であることがわかりました。 適切な解決策は、人口の十分な数の個人で非常に迅速に見つかります。 タスクを次のように設定します。

• 参照（テスト）伝達関数があります-分子：[1.5、1.0]、分母：[0.75、0.35、1.1]
• テストフィルターのゲインは1に等しく選択されました（離散フィルターを構築するときの伝達関数係数は、関数SSF :: tf2ssd-ソースのモジュール "ssf.rb"で与えられます）
• 量子化期間は0.1秒です。選択したテストフィルターの場合、十分に短い期間
• 人口の規模は、最初は350人、最大500人です。
• 反復回数-50

指定された最大数にもかかわらず、人口サイズが指定された値を超えていることが判明しました。 開始後、次の結果が得られました。

$ ruby1.9.1 main.rb

Iteration: 1

Population size: 387

best Individ: [ 1.552605923140199 1.8418549861379885 4.4154048910142265 5.556332886121151 5.320061971918478 1.6334223860651258 0.1 ]

best fitness: 2.6508867715774027

mean fitness: 1.1722382322077871

mean fitness recalc 1.1722382322077871

******************************

Iteration: 2

Population size: 421

best Individ: [ 0.37594352736713244 0.41988779230454 6.092873656120998 3.575618643442387 8.786369744495486 1.3186424599689655 0.1 ]

best fitness: 2.9780762386062767

mean fitness: 1.381001802845182

mean fitness recalc 1.381001802845182

******************************

Iteration: 3

Population size: 456

best Individ: [ 5.355702236617921 2.9021864520499134 3.979973441887163 1.1587534831116912 5.818934614234973 0.6934218845420625 0.1 ]

best fitness: 4.008150118088937

mean fitness: 1.6192001539010286

mean fitness recalc 1.6192001539010286

******************************

Iteration: 4

Population size: 501

best Individ: [ 6.981596537433821 7.0034200556235495 6.592795290155172 3.1179936580946577 7.236199584387684 1.4664747534746492 0.1 ]

best fitness: 4.629268673426835

mean fitness: 1.8244067682429481

mean fitness recalc 1.8244067682429481

******************************

Iteration: 5

Population size: 537

best Individ: [ 5.917012124258587 6.182284010197045 5.214809836688884 3.9333556599339055 8.349166334410114 1.544147649767568 0.1 ]

best fitness: 4.900537478511452

mean fitness: 2.024810983956715

mean fitness recalc 2.024810983956715

******************************

Iteration: 6

Population size: 551

best Individ: [ 5.917012124258587 6.182284010197045 5.214809836688884 3.9333556599339055 8.349166334410114 1.544147649767568 0.1 ]

best fitness: 4.900537478511452

mean fitness: 2.3489882909253152

mean fitness recalc 2.3489882909253152

******************************

Iteration: 7

Population size: 540

best Individ: [ 7.667944581517669 7.685145812466274 3.6039889820553768 2.4390348703480536 5.087422184655714 1.4689450977845646 0.1 ]

best fitness: 8.166839319133336

mean fitness: 2.652950357867813

mean fitness recalc 2.652950357867813

******************************

Iteration: 8

Population size: 552

best Individ: [ 7.667944581517669 7.685145812466274 3.6039889820553768 2.4390348703480536 5.087422184655714 1.4689450977845646 0.1 ]

best fitness: 8.166839319133336

mean fitness: 2.9467084852969725

mean fitness recalc 2.9467084852969725

******************************

Iteration: 9

Population size: 553

best Individ: [ 5.7806312313223485 4.681216450534634 5.384196754050039 3.0234885021495357 7.238140602489246 1.1815749271908358 0.1 ]

best fitness: 9.966075154360498

mean fitness: 3.335389533280396

mean fitness recalc 3.335389533280396

******************************

Iteration: 10

Population size: 543

best Individ: [ 5.7806312313223485 4.681216450534634 5.384196754050039 3.0234885021495357 7.238140602489246 1.1815749271908358 0.1 ]

best fitness: 9.966075154360498

mean fitness: 3.818330258524996

mean fitness recalc 3.818330258524996

******************************

Iteration: 11

Population size: 555

best Individ: [ 5.7806312313223485 4.681216450534634 5.384196754050039 3.0234885021495357 7.238140602489246 1.1815749271908358 0.1 ]

best fitness: 9.966075154360498

mean fitness: 4.241020711174743

mean fitness recalc 4.241020711174743

******************************

Iteration: 12

Population size: 563

best Individ: [ 7.114438733870453 5.7051128886012386 3.8495059720675098 1.8164317233081309 5.543227442940334 1.1352374472380862 0.1 ]

best fitness: 11.644557896655645

mean fitness: 4.980294253355436

mean fitness recalc 4.980294253355436

******************************

.......

******************************

Iteration: 23

Population size: 542

best Individ: [ 5.949029964618817 4.681516090696933 4.8007731550065325 2.562344672524173 6.969591955243219 1.1684490266387202 0.1 ]

best fitness: 20.468430876331446

mean fitness: 11.25191007878279

mean fitness recalc 11.25191007878279

******************************

......

******************************

Iteration: 36

Population size: 550

best Individ: [ 6.304563716617802 4.937028188768713 5.01636959411469 2.5019167234335344 7.143946485486306 1.1690443373254094 0.1 ]

best fitness: 30.361894930102864

mean fitness: 22.65217005076974

mean fitness recalc 22.65217005076974

******************************

........

******************************

Iteration: 46

Population size: 542

best Individ: [ 6.548169493382168 5.060607979367818 4.739775170940725 2.3444848651883947 6.741642980854007 1.1564890916088506 0.1 ]

best fitness: 32.826565607333514

mean fitness: 25.606090666108418

mean fitness recalc 25.606090666108418

******************************

Iteration: 47

Population size: 550

best Individ: [ 6.548169493382168 5.060607979367818 4.739775170940725 2.3444848651883947 6.741642980854007 1.1564890916088506 0.1 ]

best fitness: 32.826565607333514

mean fitness: 25.489911664932283

mean fitness recalc 25.489911664932283

******************************

Iteration: 48

Population size: 561

best Individ: [ 6.548169493382168 5.060607979367818 4.739775170940725 2.3444848651883947 6.741642980854007 1.1564890916088506 0.1 ]

best fitness: 32.826565607333514

mean fitness: 25.44926190395142

mean fitness recalc 25.44926190395142

******************************

Iteration: 49

Population size: 550

best Individ: [ 3.1439340250602816 5.060607979367818 4.739775170940725 2.3444848651883947 6.741642980854007 1.1564890916088506 0.1 ]

best fitness: 32.826565607333514

mean fitness: 26.108921277427932

mean fitness recalc 26.108921277427932

******************************

Iteration: 50

Population size: 559

best Individ: [ 3.1439340250602816 5.060607979367818 4.739775170940725 2.3444848651883947 6.741642980854007 1.1564890916088506 0.1 ]

best fitness: 32.826565607333514

mean fitness: 26.23635084771665

mean fitness recalc 26.23635084771665

******************************





「Best Individ」の最初の2つの数字は伝達関数の分子、次の3つは分母、次にスケール係数と量子化期間です。 32の「オウム」に等しい最高のフィットネスは、かなり良い結果です。 次の図のサポート：



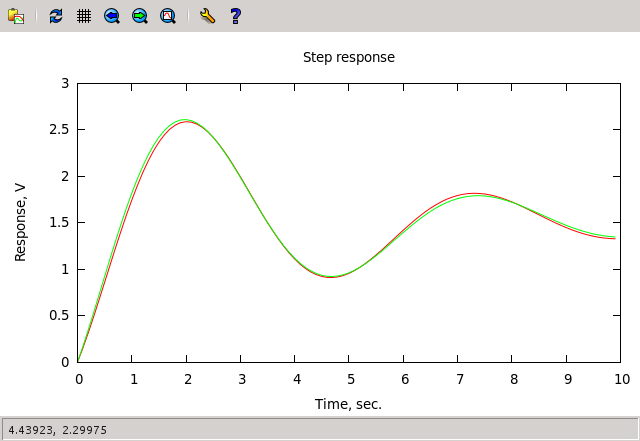
これは、テストの過渡現象のグラフを示しており、入力でシングルステップ効果がフィルターに適用されたときにフィルターの進化中に取得されます。 「Who」チャートから「Who」とはまだ言えません-gnuplotを使用するための機能はまだ完了していませんが、この場合も重要ではありません。 肉眼では、結果が非​​常に近いことが明らかです。

おわりに

このプログラムは、「U.M.N.I.K。」プログラムの下で研究の過程で実施されました。 コードは未加工ですが動作しています（少なくとも私にとって）。 利便性のために、プログラムにいくつかのシンプルなGUIを装備する計画があります。 以下はコードへのリンクです。

UPD1：ソースコードはGitHubでホストされています。

GitHubリポジトリ