CUDAでO（N）の配列をソートします

はじめに

どういうわけか、タスクは、最小限のコードと可能な限り高速のGPUを使用して、文字列の一意の配列をソートすることでした...

この投稿では、そのソリューションの主なアイデアを説明します。 この投稿のソート配列の要素は数字です。

小さな配列のユニークな要素を持つケース

CUDAは、ブランドまたは個人と見なされる理由からプラットフォームとして選択されました。 実際、CUDAには具体的に多くの例があります。現在、ATIやOpenCLの同様のプラットフォームよりもGPUコンピューティングで開発されています。

CUDAソートアルゴリズムのネットワーク検索では、異なる結果が得られました。 これが最も興味深いものです。 図面があります



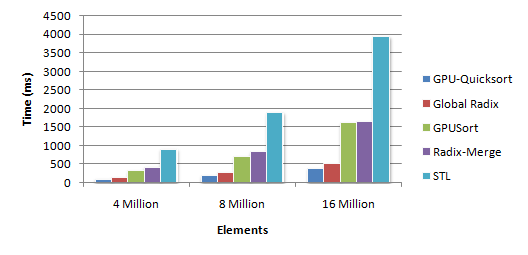
これは、O（NlogN）からO（N ^ 2）までの順序の複雑さを与えるQSORTアルゴリズムによって最良の結果が得られたことを示しています。 この記事ではGPUでの並列化が最良の結果をもたらしましたが、QSORTがこのタスクにビデオカードのリソースを使用する最良の方法ではないという疑問がありました（特定のコードのサイズが特に怖かった）。 以下では、問題の解決方法について説明します。最悪の場合は、基本的に O（N）の時間の複雑 さを伴う「1行」です。





だから、我々は何を持っている：現代のビデオカードは500 * 32以上のスレッド（GTX275）、約15,000、同時に動作しています。

私が持っていたソートタスクの条件は次のとおりでした：最大1000要素の配列（以下、大きな値を持つ一般的なケースが考慮されますが、私は持っていました）。 このような配列をO（NlogN）時間でソートし、15,000スレッドを使用することは、なんとなく無駄に思えました。



パピルスの推論の結果、最高の速度を達成するために、これがO（N）であるためには、同時に動作する各スレッドがO（N）以下の操作を実行する必要があることがわかりました。 つまり、一度配列に渡されます。 そして、パスの結果は、結果のソート済み配列内の1つの要素の位置を決定するキーでなければなりません。

独自のスレッド番号tid（通常は0..MaxThreads-1から）を知っているため、結果としてtid要素の位置を見つけるというアイデアが使用されました。



元の配列をA [] = {1,5,2,4,7} として、各スレッドのタスクを設定して、結果の配列B []の要素A [tid]の位置を見つけます 。



これを行うために、補助配列K []-結果として要素A [tid]の位置を開始します。 ArraySize-A []の要素の数。

現在、 ソースコード自体は、 CUDA \ C（.cuファイル）で提案されているアルゴリズムの実装のフラグメントです。

1. MainKernel ( kernel.cu) ArraySize .

MainKernel <<<grids, threads>>> (A,B,ArraySize,MaxThreads);



2. CUDA- MainKernel ( kernel.cu) A[], ArraySize, MaxThreads, B[] K[].

unsigned long tid = blockIdx.x*blockDim.x + threadIdx.x; //

for (unsigned long i = 0;i<ArraySize;++i) // O(N)

if (A[i]<A[tid])

++K[tid]; // O(1)



3. __syncthreads(); // , .. tid-



4. B[K[tid]] = A[tid]; // ( O(1), 3 qsort, swap ..)

* , K[]={0,0,2,3,4}.

.4 , ( O(1)). .







そして、利用可能なスレッドの数がN以上であれば、結果の配列B []はO（N）でソートされます。



大きな配列の一意の要素を持つケース

配列の次元を増やすと、同じアプローチを使用できます。1つのスレッドだけが位置を探します

for [ArraySize / MaxThreads]-（除算の整数部分）要素。 この場合、アルゴリズムの実行時間は[ArraySize / MaxThreads] * O（N）に変更されます。つまり、配列内の要素が使用可能なスレッドの数を超える数になります。



この場合、アルゴリズムの実装は次の形式を取ります。

1. MainKernel ( kernel.cu) [ArraySize/MaxThreads] .

MainKernel <<<grids, threads>>> (A,B,ArraySize,MaxThreads);



2. CUDA- MainKernel ( kernel.cu) A[], ArraySize, MaxThreads, B[] K[].

unsigned long tid = blockIdx.x*blockDim.x + threadIdx.x; //



2.5. , .

unsigned long c = ArraySize/MaxThreads;

for (unsigned long j = 0;j<c;++j) {

unsigned int ttid = c*tid + j; // -



for (unsigned long i = 0;i<ArraySize;++i)

if (A[i]<A[ttid])

++K[ttid]; //



3. __syncthreads(); // , .. tid-



4. B[K[ttid]] = A[ttid]; //

} //







結論1

1行に記述された、tidの番号を持つ1つのストリームの最終的なソートアルゴリズムの約束：

for (unsigned long i = 0;i<ArraySize;++i) if (A[i]<A[tid]) ++K[tid];





A [i]-並べ替えられていない配列。 これで、K [tid]-結果としてソース要素の位置インデックスが含まれます。 並べ替え順序は、B [K [tid]] = A [tid]とB [ArraySize-K [tid] -1] = A [tid]のいずれかを選択することで簡単に変更できます。



最初からのデータの例

A [] = {1,5,2,4,7}。 ArraySize =5。フローを開始します5。

ストリーム0。tid=0。K[tid] = K [0]をA [tid] = A [0] = 1：K [0] = 0に設定

ストリーム1. tid =1。K[tid] = K [1]をA [tid] = A [1] = 5に設定します。K[1] = 3

ストリーム2. tid = 2. A [2] = 2。 K [2] = 1

ストリーム3. tid = 3. A [3] = 4。 K [3] = 2

ストリーム4. tid =4。A[4] = 7。 K [4] = 4

それだけです さて、すべてのスレッドが同時に実行されていたため、配列（O（N））のソートのみに時間を費やしました。 そして、彼らはK [] = {0,3,1,2,4}を得ました。



特徴

[ArraySize / MaxThreads]が非常に大きい >> ArraySizeの場合、このアルゴリズムはO（N ^ 2）より大きな複雑度を取ります。

また、元の配列の要素が一意であるかどうかが事前にわからない場合は、使用しないことをお勧めします。



結論2

したがって、元の問題は、最悪の場合のO（N）と最高の場合のO（N）について解決されました（もちろん、加速はNフローのみによるものでした）。 そして、利用可能なスレッドの数が、ソートされた配列の要素の数より少なくないことを条件とします。



この投稿は、初心者アルゴリズム研究者がGPGPUで高速コンピューティングを行うための興味深い概念ソリューションを作成するのに役立つはずです。 文献から、コーメンのアルゴリズムの本と、projecteuler.netの興味深いタスクへのポータルに注目しています。



UPD1。 （2010/12/17 1:40 PM）

その過程で、元の配列A []が16KBのメモリを占有する場合、まだ保存する必要があり、結果B []は__shared__メモリで機能しません （計算を高速化するためにCUDAでレベル2キャッシュとして使用します） __shared__のサイズは16KBのみです（GTX275の場合）。

したがって、アルゴリズムは「並列スワップ」で補完され、結果は元のA []になります。

1. for (unsigned long i = 0;i<ArraySize;i++)

if (A[i]<A[tid])

K[tid]++; //



2. __syncthreads(); // !



3. unsigned long B_tid = A[tid]; //, ""



4. __syncthreads(); // ""



5. A[K[tid]] = B_tid; //





これで、元の配列A []はより少ないメモリを使用してソートされました。



UPD2。 （2010/12/17 16:34、 対象 ）

__shared__メモリへのアクセスが少なくなり、わずかな最適化が行われるため、オプションが高速になります。

0. unsigned int K_tid = 0;



1. unsigned long B_tid = A[tid]; //, ""



2. for (unsigned long i = 0;i<ArraySize;++i)

if (A[i]<B_tid)

++K_tid; //



3. __syncthreads(); // ""



4. A[K_tid] = B_tid; //







UPD3 。（ 12.20.2010 14:16）例のソースコードを提供します： main.cpp 、 kernel.cu （配列のサイズはビデオカードの__shared__メモリ内でなければなりません）。



UPD4 。（12/23/2010 2:56 PM）複雑さO（N）に関して：提案されたアルゴリズムは、 線形時間の複雑さΘ（n + k） ©Wiki。