ネットワークの最大フローを見つけるためのアルゴリズムを適用する方法
はじめに
最大流量の問題は古典的なものであり、多くの用途があります。 問題文を思い出させてください。 非負の重み(スループット)を持つ重み付き有向グラフが提供されます。 2つの頂点が区別されます。ソースSとシンクTです。他の頂点はSからTへのパス上にあります。 フローは関数F:V x Vなどのプロパティです
- 帯域幅制限。 エッジに沿ったフローは、その(エッジ)スループットを超えることはできません。
- 非対称性。 各エッジ(u、v):F(u、v)= -F(v、u)。
- ストリームを保存しています。 各頂点( SおよびTを除く)の場合、着信ストリームの量(負)は発信ストリームの数(正)に等しくなります。 つまり、各頂点のフローの代数和( SとTを除く)はゼロです。
この投稿では、問題の実装に慣れることができます。
ネットワーク内の最大フローを見つけるためのアルゴリズムに還元される典型的なタスクに直接進みます。 そのようなタスクのフローを識別することは、多くの場合簡単ではありません。
タスク
- 最大一致の問題。 入り口では、N-男の子の数、M-女の子の数と、どの男の子と一緒に踊りたい男の子のリスト(複数の場合があります)が与えられます。 同時に踊るカップルの最大数を決定する必要があります。
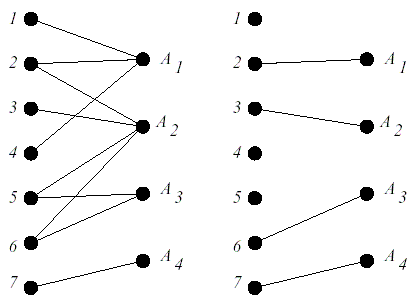
解決策
この問題を解決するには、Kuhnアルゴリズムを使用できますが、すべてをストリームに還元し始めたので、やってみましょう。 このため、十分なソースとドレインがありません。 それらを追加しましょう! 「左側」では、架空の頂点を追加し、体重1のすべての男の子にrib骨を描きます。男の子から女の子まで、rib骨があり、同じ価格になります。1。女の子のrib骨から排水口までもコストがかかります。 。 - 寄木細工の損傷。 NxMフローリングでは、一部のセルが破損している可能性があります。 それらは新しいタイルで覆われている必要があります。 タイルのサイズは2x1(回転はできますが、カットできません)はAの価格で、1x1はBの価格です。問題は、汚された寄木細工のタイルを敷くために費やす必要のある最小量です。 当然、新しいタイルは他のタイルと重ならないようにしてください。
解決策
まず、2 * B> Aであることを確認します。 それ以外の場合、1x1タイルのみをタイル化する方が収益性が高く、検討する必要はありません。 次に、タスクはAの価格でタイルの数を最大化することです。
チェス盤の原理で寄木細工を着色します。 明らかに、2x1タイルの一方の端は黒いケージに、もう一方の端は白に置かれます。 したがって、2つの部分からなるグラフを作成します。その1つの部分には白いセルが含まれ、もう1つの部分には黒いセルが含まれます。 隣接するセルの間に重量1のrib骨を描きます。 無限大の白いピークにエッジのあるソース(かなり一般的なトリック)と、無限大の黒いセルのエッジのあるドレインを追加します。 fをソースとドレインの間にある最大流量の値とする。 つまり、タイルの数は2x1でした。 問題の答えはf * A +(Kf)* Bです。ここで、Kは損傷した細胞の総数です。
出典:ハリコフウィンタープログラミングスクール、2009年、3日目
- ペイントのタスク。 セルが黒または白に塗られたN * Mマトリックスを考える。 Wは黒の正方形を白、B-白を黒に塗り替える価格です。 再描画後、異なる色のすべての隣接する正方形の間に、Gの価格で灰色の線を描画する必要があります。最小量を費やすために、マトリックスを非常に高速に再描画する(または何もしない)必要があります。

解決策
極端な場合:マトリックスがすべて同じ色の場合-答えは0です。
ダミーのソースとストックを追加します。 ソースからすべての白いピークまで、Bで重み付けされたエッジを描画します(黒への再描画の価格)。 黒い山から排水口まで、幅がWのrib骨を描きます(白への塗り直しの価格)。 そして、すべての隣接する頂点の間(同じ色であるか、異なる色であるか)-G(灰色の線)に重さのあるエッジを置きます。 最大流量の大きさが問題の答えになります。
出典:情報学の全ウクライナ学校オリンピック、2007年、1日目
- 頂点の制約に関する問題。 最大流量を見つけ、ピークがどれだけ見逃すことができるかを制限する必要があるとします。
解決策
必要なのは、各頂点を2つに分割し、それらの間にエッジを配置して、この頂点の帯域幅制限を考慮することです。 - 最小カット。 ダン・カウント。 AからBへのパスがなくなるように、頂点をいくつ削除する必要がありますか?
解決策
古典的な最小カット問題では、エッジを削除する必要があります。 問題ありません! 頂点を2に分割し、それらの間にエッジを置き、1の重みを付けます。その後、問題の答えは、グラフの最小カット(最大フロー)を見つけることです。
出典:ハリコフウィンタープログラミングスクール、2009年、3日目
- 詩の作家。 1つの初期状態Aと1つの最終Bを備えた決定論的な有限状態マシンがあります。各遷移は、3つの数値(i、j、k)、エッジkに沿った状態iから状態jへの遷移によって定義されます。
エッジkに沿ったiからjへのオートマトンを通過した後、エッジkに沿ったiからjへのすべての遷移だけでなく、エッジkに沿ったiからのすべての遷移も消去されます。 そのようなオートマトンによってAからBへのパスの数を推定する必要があります。
解決策
タスクはパスの最大数を見つけることであり、同じ色の複数のエッジが1つの頂点から出て行くことはありません。 問題を減らして、最大流量を見つけます。 各頂点について、再構築されたネットワークにk + 1の頂点を作成します。 最初の頂点が入力になり、残りの頂点が色を表します。 入口の上部から、色に対応するk個の頂点のそれぞれに1のスループットでエッジを描画します。 色iに対応する頂点から、色iのすべてのエッジを、エッジの端の入力に描画します。 このようなネットワークで最大のフローを見つけたので、必要なプロパティを満たすパスの最大数を取得します。
出典:ハリコフウィンタープログラミングスクール、2009年4日目
- コイン収集。 n個のコレクターとm種類のコインがあります。 クラブに参加するには、各タイプのコインを少なくとも1枚持っている必要があります。 あなた(1番)は、利用可能なコインをコレクターと交換できます。 タイプaのコインが複数あり、タイプbのコインが1つもない場合、コレクターはコインaをあなたのコインbと交換します。 また、あなたはこの規則に違反する可能性があります。 すべてのコレクターの既知の状況から、できるだけ多くの種類のコインを収集する必要があります。
解決策
ネットワークを構築します。 コインの種類ごとに、頂点を1つ作成します。 これらのトップスはあなたのコインと一致します。 できるだけ多くの一意のコインを収集する必要があります。そのため、そのような各頂点からドレインに帯域幅エッジ1を描画します。 最初に持っているコインに対応する頂点に、そのようなコインの数に等しいスループットを持つエッジを描画します。
クラブの各メンバー(1を除く、つまりあなた)には、1つの頂点があります。 この頂点は、コインを1つしかとることができません。
k-1コイン以下で、そのうちk個(k> 1)を持っています。 当然、クラブのメンバーは受け取ったコイン1枚と引き換えにコイン1枚を贈ります。
したがって、このような各頂点で、このクラブメンバーが持っていないコインに対応する頂点の帯域幅エッジ1を描画する必要があります。 そして、これらの頂点から、クラブメンバーが複数持っているコインに対応する頂点iにk i -1の帯域幅を持つエッジを描く必要があります。
構築されたネットワークは、クラブでの交換プロセスを反映しています。 このようなネットワークでの最大フローは、収集可能なコインの最大数に等しくなります。
出典:ハリコフウィンタープログラミングスクール、2009年4日目
- 循環。 原子炉冷却システムは、ノードを接続するパイプのセットです。 液体はパイプを流れ、各パイプについて、液体が流れる方向が厳密に定義されています。 冷却システムのノードには1からNまでの番号が付けられています。冷却システムは、ノードごとに単位時間、ノードに流入する液体の量がノードから流れる液体の量と等しくなるように設計する必要があります。 各パイプにはスループットc ijがあります。 さらに、十分な冷却を確保するには、単位時間あたり少なくともl ij単位の流体がパイプを流れることが必要です。 つまり、i番目のノードからj番目のノードにつながるパイプの場合、l ij≤f ij≤c ijを満たす必要があります。
冷却システムの説明が記載されています。 指示された条件がすべて満たされるように、液体をパイプに流す方法を見つける必要があります。
解決策
これは、エッジに与えられたより低い制限でネットワーク内の循環を見つける問題です。 ストリームがセグメント[l、r]のエッジ(u、v)を通過する必要がある場合、再構築されたネットワークには3つのエッジ(場所、場所、重み)があります:(u、v、r-l)、(S、v、l )、(u、T、l)。 S、Tは、それぞれ追加で導入されたシンクとソースです。 実際、必要な最小流量をエッジに沿って通過させ、それを循環させて循環を確保します。
出典:ハリコフウィンタープログラミングスクール、2009年4日目
- 再び踊る。 N人の男の子とN人の女の子がパーティーに招待されます。 彼らは数ラウンド踊りたいと思っています。
各ラウンドでは、ゲストはn個のダンスカップルに分割されます。 各ゲストはペアになっている必要があり、各ペアは男の子と女の子で構成されている必要があります。 各ラウンドで、各男の子は異なる女の子と踊らなければなりません。 一部の男の子と女の子はお互いが好きではありません。 各少年は、彼が好きではないk人以下の少女と踊ることができます。 同様に、各女の子は、自分が嫌いな男の子をk人以下で踊ることができます。
i番目の少年とj番目の少女(1≤i、j≤n)が互いに似ているかどうかに関する情報があります。 パーティーで踊ることができるラウンドの最大数を見つけます。
解決策
次の問題を考慮してください。正確にmラウンドで踊り続けることができますか? この質問に答えることができれば、二分探索によって、ダンスが可能な最大のmを見つけます。
1つのソースと1つのシンク(黒い頂点)を持つグラフを作成します。 赤いピークは男の子を表し、グレーのピークは女の子を表します。 男の子と女の子がお互いに似ている場合、それらの間にユニット容量のエッジを描画します(図では、これらは2つのエッジ-上部と下部)。 それ以外の場合は、図に示すように青と緑の頂点を追加し、対応する青と緑の頂点間のエッジの帯域幅を1に設定します。
青と緑のピークが「保護」レベルを形成します。 互いに嫌いな女の子と男の子のつながりは、保護レベルの端に沿って進みます。 各少年は、彼が好きではないk人以下の少女と踊ることができます。 赤と青、緑と灰色のピーク間のエッジの帯域幅をkに設定します。 したがって、各男の子と各女の子の間で、直接または保護レベルのピークを通してエッジを介して接続が確立されます。
ダンスは正確にmラウンド続けなければなりません。 ソースと赤いピークの間、およびグレーのピークとドレインの間のエッジの帯域幅をmに等しく設定します。

グラフで最大流量を見つけます。 最大流量がn * m(nは男の子の数)に等しい場合に限り、ダンスは正確にmラウンドで続行できます。
出典:Sevastopol Summer Programming School、2010、4日目
おわりに
私たちは、ネットワーク内の最大フローを見つけることまで煮詰める膨大な一連のタスクの無視できる部分を検討しました。 そして、これは最小コストの最大フローには影響しません。 このようなタスクは、解決の美しさによって区別されます。 最大フローを見つけるための標準アルゴリズムを知っているプログラマは、タスクに対応するグラフを作成してフローを開始することしかできません。
All Articles