デカルトツリー：パート3.暗黙的なキーによるデカルトツリー

目次（現在）

パート1.説明、操作、アプリケーション。

パート2。ツリー内の貴重な情報とそれによる複数の操作。

パート3.暗黙的なキーによるデカルトツリー。

続行するには...

非常に強い魔術

デカルトの木が前の2つの部分で私たちに与えたすべての機会の後、今日私は彼と奇妙で神聖な何かをします。 それにもかかわらず、このアクションにより、完全に新しい停滞状態にあるツリーを、追加機能を備えた高度で強力な配列の一種として考えることができます。 その操作方法を示し、2番目の部分のデータを使用したすべての操作が変更されたツリー用に保存されることを示し、その後、いくつかの新しい有用なものを提供します。



デラミドの構造をもう一度思い出してください。 これには、デラミドが検索ツリーであるキーx 、デラミドが束であるランダムキーy 、および場合によっては（コスト）を持つユーザー情報も含まれます。 キーxなしで不可能なことを行い、デラミドを考えてみましょう。 つまり、キーxがまったくなく、キーyがランダムなツリーができます。 したがって、なぜそれが必要なのかは一般的に理解できません:)



実際、そのような構造を考慮することは、キーxがまだどこかに存在するデカルトツリーのようなものですが、それらは私たちに通知されませんでした。 しかし、彼らは彼らのために、予想通り、二分探索木の条件が満たされていると誓います。 次に、これらの未知のXは0からN-1までの数字であり、ツリーの構造に従って暗黙的に配置されると想像できます。







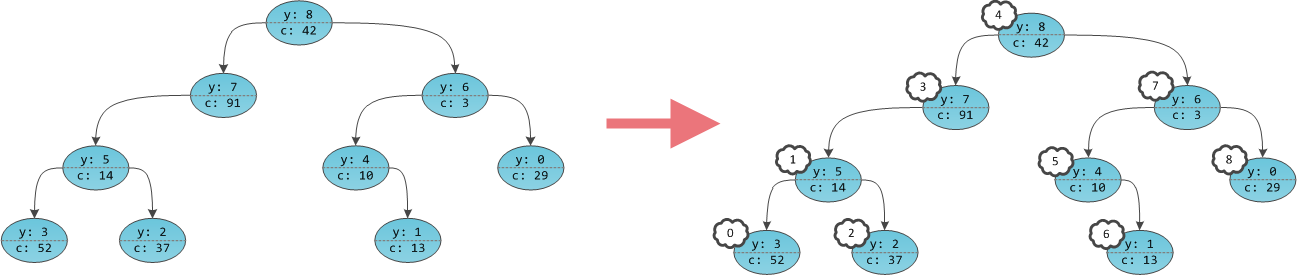
ツリーでは、頂点のキーが付加されていないように見えますが、頂点自体には番号が付けられています。 さらに、それらは、最後の部分からすでにおなじみの順序通りのバイパス順序で番号が付けられています。 明確に番号付けされた頂点を持つツリーは、インデックスが同じ暗黙的なキーであり、コンテンツがユーザー情報c



である配列と見なすことができます。 プレーヤーは、バランスを取るためにのみ必要です;これらは、ユーザーにとって不要なデータ構造の内部的な詳細です。 X は実際には原則的には格納されていません。







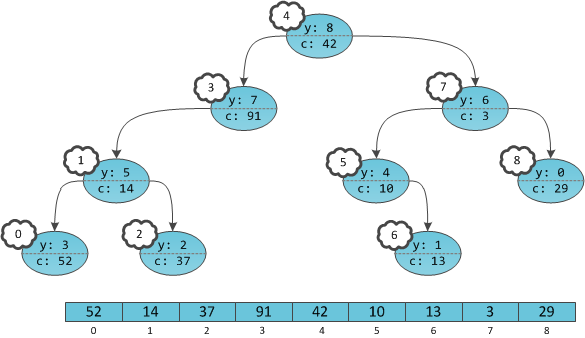
前の部分とは異なり、この配列はソートなどのプロパティを自動的に取得しません。 結局のところ、情報に関する構造上の制限はなく、とにかく最上部に保存できます。

主な用途

さて、なぜそのような解釈が必要なのかについて話す価値はあります。

たとえば、2つの配列をマージしたいと思ったことはありますか？ つまり、ループ内のO（N）にある2番目の要素のすべての要素をコピーすることなく、単純に1つの要素を他の要素の最後に割り当てるだけです。 暗黙的なキーによるデカルトツリーを使用すると、このような機会が得られます。結局のところ、Merge操作を私たちから奪った人はいません。



Stop-stop-stopですが、Mergeは明示的なデカルトツリー用に作成されました。 彼女のアルゴリズムはここで作り直さなければならないでしょうか？ そうでもない。 彼女のコードをもう一度見てください。

 public static Treap Merge(Treap L, Treap R) { if (L == null) return R; if (R == null) return L; if (Ly > Ry) { var newR = Merge(L.Right, R); return new Treap(Lx, Ly, L.Left, newR); } else { var newL = Merge(L, R.Left); return new Treap(Rx, Ry, newL, R.Right); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

思い出すように、マージ操作は、左入力ツリーLのすべてのキーが右入力ツリーRのキーを超えないという事実に依存しています。 この条件が満たされるという仮定の下で、原則としてキーに注意を払わずにマージします。アルゴリズムを実行するプロセスでは、優先順位のみが比較されます。



あなたと私はここで最もoperation慢な方法でマージ操作を欺いていることがわかります：彼女は順序付けられたキーを持つツリーが与えられることを期待しています、そして私たちはキーなしでツリーからヤシを取り除きます:)しかし、ツリーに明示的なキーがあり、順序付けられているという仮定は彼女を強制します検索ツリーの条件を満たさなければならないため、キーLがキーRよりも何らかの意味でツリー構造内にあるようにツリーをマージします。 つまり、ツリーLにN個の要素があり、ツリーRにそれぞれM個の要素がある場合、ツリーRの要素をマージすると、NからN + M-1までの暗黙の数が自動的に取得されます。 ツリー構造によれば、マージ操作は自動的にそれらを適切に配布し、考慮される優先順位は「準バランス」を実行します。 したがって、「配列」Rを「配列」Lの右側に「帰属」させました。



ソースに関しては、 x



キーなしで新しいImplicitTreap



データ型を取得するだけでよく、それに対応するプライベートコンストラクターが必要です。 すべてのマージコードは同じままです。 もちろん、これはここに複数のクエリを計算しないバージョンであると考える場合です。2番目の部分で実装された「正義の回復」および「プッシュ約束」の機能も古い場所のMergeに残ります。



明確にするために、2つのランダムな暗黙のデカルトツリーを取得し、マージ結果とともに図に示します。 優先順位はランダムに選択されるため、両方のツリーの実際の構造と結果は非常に異なる場合があります。 しかし、それは重要ではありません-配列の構造、つまり 要素c



のシーケンスは常に保持されます。

オレンジ色の矢印は、Mergeの再帰パスです。









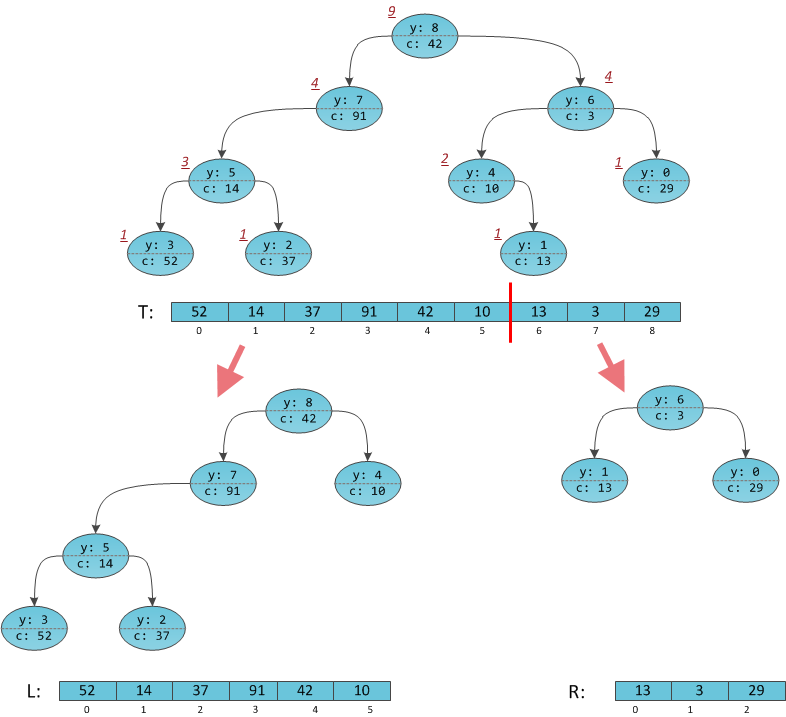
今、分割する時間です。 彼女を欺くのはそれほど簡単ではありません。逆に、スプリット操作は優先順位に関心がなく、キーを比較するだけです。 暗黙のツリーのピークを彼女がどのように比較するかについて考える必要があります。 問題は実際にはより高いものですが、新しいデータ構造で分割操作は何をしますか？ 彼女はかつてキーで木を切りましたが、ここには切り取る必要のあるキーがありません。



キーはありませんが、それらの暗黙的な表現-配列インデックスがあります。 したがって、切り取りの本質はいくらか変更されました。正確にx _0の要素が左側に、他のすべてが右側に表示されるように、ツリーを2つに分割します。 「大規模な」解釈では、これは配列の先頭からx _0個の要素を新しい配列に分離することを意味します。



新しい分割操作を実行する方法は？ 前と同じように、彼女は2つのケースを検討します。ルートTは左の結果Lまたは右のRに表示されます。 配列内のインデックスがx ₀より小さい場合は左に表示され、そうでない場合は右に表示されます。 そして、配列内のツリーの最上部のインデックスは何ですか？ 私たちはすでに、2番目のパートから彼との作業方法を知っています。 サブツリーのサイズをツリーの最上部に格納するだけで十分です。 その後、選択プロセスは簡単に復元されます。



S _Lを左サブツリーのサイズ（ T.Left.Size



）とします。

S _L +1≤x _0の場合、ルートは左の結果になります。 そのため、正しいサブツリーを再帰的にカットする必要があります。 ただし、別のキー、 x ₀ -S _L -1でカットします。これは、 S _L +1の要素がすでに目的の左の結果になっているためです。

S _L +1> x _0の場合、ルートは正しい結果になります。 次に、左側のサブツリーを再帰的にカットする必要があります。 この場合、以前のように完全に対称的ではありません。このステップでは、再帰によって要素が左の結果ではなく右の結果に分割されるため、サブツリーをすべて同じキーx ₀でカットします。



この図は、サブツリーが添付され、 x ₀ = 6に分割されたデカルトツリーを示しています。







新しいスプリットのソースコードは、新しいクラスのワークピースと一緒にキーレスであり、別のプライベートコンストラクターを備えています。

これまでのところ、複数の操作を行わずにSplitを再度提供しています。読者はこれらの行を個別に復元できますが、古い場所からは消えていません。 しかし、サブツリーのサイズを再カウントすることを忘れてはなりません。

 private int y; public double Cost; public ImplicitTreap Left; public ImplicitTreap Right; public int Size = 1; private ImplicitTreap(int y, double cost, ImplicitTreap left = null, ImplicitTreap right = null) { this.y = y; this.Cost = cost; this.Left = left; this.Right = right; } public static int SizeOf(ImplicitTreap treap) { return treap == null ? 0 : treap.Size; } public void Recalc() { Size = SizeOf(Left) + SizeOf(Right) + 1; } //    -  Split public void Split(int x, out ImplicitTreap L, out ImplicitTreap R) { ImplicitTreap newTree = null; int curIndex = SizeOf(Left) + 1; if (curIndex <= x) { if (Right == null) R = null; else Right.Split(x - curIndex, out newTree, out R); L = new ImplicitTreap(y, Cost, Left, newTree); L.Recalc(); } else { if (Left == null) L = null; else Left.Split(x, out L, out newTree); R = new ImplicitTreap(y, Cost, newTree, Right); R.Recalc(); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

対数時間で動作するSplitとMergeの配列を作成したので、それらをどこかで使用します。 配列をいじってみましょう。

配列のあるゲーム

挿入

フォーカスNo. 1-通常どおり、O（N）ではなくO（log ₂ N）の必要な位置Posに要素を配列内に挿入します。



原則として、通常のデカルトツリーでこれを行う方法は既にわかっていますが、今ではキーがインデックスに置き換えられています。 そして、残りの手順は変更されていません。



•配列T [0;をカットします。 N）配列のインデックスPos L [0; Pos）およびR [Pos; N） 。

•挿入された要素の1つの頂点から配列ツリーを作成します。

•作成された配列を右から左の結果Lに割り当て、両方に右の結果Rを割り当てます。

• T '[0;の配列を取得しました。 N + 1） 、目的の要素は位置Posにあり、右側の残りの部分がシフトされます。



挿入のソースコードは完全には変更されていません。

 public ImplicitTreap Add(int pos, double elemCost) { ImplicitTreap l, r; Split(pos, out l, out r); ImplicitTreap m = new ImplicitTreap(rand.Next(), elemCost); return Merge(Merge(l, m), r); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

削除する

フォーカスNo. 2-この位置Posにある配列から要素を切り取ります。



繰り返しますが、手順は通常のデカルト木と同じです。



•配列T [0;をカットします。 N）配列のインデックスPos L [0; Pos）およびR [Pos; N） 。

•正しい結果Rは、インデックス1（単位！）でカットされます。 配列Mを取得します[Pos; Pos + 1） 1つの要素（以前にPos位置に立っていた）、および配列R '[Pos + 1; N） 。

•配列LとR 'をマージします。



ソースコードのダウンロード：

 public ImplicitTreap Remove(int pos) { ImplicitTreap l, m, r; Split(pos, out l, out r); r.Split(1, out m, out r); return Merge(l, r); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

セグメントごとに複数のリクエスト

フォーカスNo.3：O（log ₂ N）の場合、配列サブセグメントですべて同じクエリを実行できます（合計/最大/最小/存在またはラベル数など）。



ツリー構造は前の部分から変更されません。頂点には、サブセグメント全体に対して計算された目的の値に対応するパラメーターが格納されます。 MergeとSplitの最後に、同じRecalc()



呼び出しがRecalc()



、その子孫の計算されたパラメーターに基づいて頂点の値の値を再計算します。



セグメントのリクエスト[A; B）標準的な方法を使用します：配列から目的のセグメントを切り取ります（最初の切り取りの後、正しい結果の目的のインデックスが減少したことを忘れないでください！）そして、そのルートに格納されているパラメーターの値を返します。

ソースコード-例として、最大。

 public double MaxTreeCost; public static double CostOf(ImplicitTreap treap) { return treap == null ? double.NegativeInfinity : treap.MaxTreeCost; } public void Recalc() { Size = SizeOf(Left) + SizeOf(Right) + 1; MaxTreeCost = Math.Max(Cost, Math.Max(CostOf(Left), CostOf(Right))); } public double MaxCostOn(int A, int B) { ImplicitTreap l, m, r; this.Split(A, out l, out r); r.Split(B - A, out m, out r); return CostOf(m); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

セグメント上の複数の操作

フォーカスNo.4：O（log ₂ N）の場合、配列のサブセグメントの2番目の部分から操作を実行します：定数の追加、ペイント、単一値への設定など。



MergeとSplitを使用すると、デカルトツリーでの遅延計算の実装はまったく変更されません。 仕事の基本原則は同じです。操作を実行する前に、子孫に「約束を押します」。 前のセクションの複数のクエリもサポートする必要がある場合は、操作の完了後に「正義を復元する」必要があります。



セグメントで操作を実行するには、最初に2つのSplit呼び出しでこのセグメントをツリーから切り取り、2つのMerge呼び出しで再度貼り付ける必要があります。

怠け者のために、追加の完全なソースコードと、新しいMerge / Splitの実装（1〜2行も異なります）、およびPush



プッシュ機能を提供します。

 public double Add; public static void Push(ImplicitTreap treap) { if (treap == null) return; treap.Cost += treap.Add; if (treap.Left != null) treap.Left.Add += treap.Add; if (treap.Right != null) treap.Right.Add += treap.Add; treap.Add = 0; } public void Recalc() { Size = SizeOf(Left) + SizeOf(Right) + 1; } public static ImplicitTreap Merge(ImplicitTreap L, ImplicitTreap R) { // ! Push( L ); Push( R ); if (L == null) return R; if (R == null) return L; ImplicitTreap answer; if (Ly > Ry) { var newR = Merge(L.Right, R); answer = new ImplicitTreap(Ly, L.Cost, L.Left, newR); } else { var newL = Merge(L, R.Left); answer = new ImplicitTreap(Ry, R.Cost, newL, R.Right); } answer.Recalc(); return answer; } public void Split(int x, out ImplicitTreap L, out ImplicitTreap R) { Push(this); // ! ImplicitTreap newTree = null; int curIndex = SizeOf(Left) + 1; if (curIndex <= x) { if (Right == null) R = null; else Right.Split(x - curIndex, out newTree, out R); L = new ImplicitTreap(y, Cost, Left, newTree); L.Recalc(); } else { if (Left == null) L = null; else Left.Split(x, out L, out newTree); R = new ImplicitTreap(y, Cost, newTree, Right); R.Recalc(); } } public ImplicitTreap IncCostOn(int A, int B, double Delta) { ImplicitTreap l, m, r; this.Split(A, out l, out r); r.Split(B - A, out m, out r); m.Add += Delta; return Merge(Merge(l, m), r); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

許可された操作に関する小さな余談：

実際、再帰的なツリー構造と遅延計算により、モノイド操作を実装できます。 モノイドは、バイナリ演算◦が指定されたセットであり、次のプロパティがあります。

•結合性-任意の要素a、b、cに対して（a◦b）◦c = a◦（b◦c）があります。

•中立要素の存在-セットには要素eがあり、任意の要素aに対して◦e = e◦a = aです。

次に、このような操作のために、セグメントのツリー 、および同様の理由でデカルトツリーを実装することができます。

配列を反転

フォーカスNo. 5は、サブセグメントフリップです。つまり、要素を逆順に並べ替えます。



そして、この時点で私はより詳細に停止します。 配列を回転させることは、モノイダル操作ではありません-率直に言って、それはどのセットでもバイナリ操作ではありません-それにもかかわらずです。 このタスクの独自性は、そのためのプッシュ機能を思いつくことができるということです。 また、オペレーションをプッシュする機会があるため、遅延オペレーションとして実現できることを意味します。



そのため、各頂点にブール値（格納ビット）を格納します。 これは、「アレイのこのセグメントを将来的に展開する必要がある」という延期された約束です。 次に、このビットをPush



関数の特異なバージョンで子孫にプッシュできると仮定すると、ツリーは常に最新の状態に保たれます-配列要素にアクセスする（検索）操作の前、およびマージと分割の開始時にプッシュが実行されます。 この「約束の履行」をどのように実現するかを理解することは残っています。



ある頂点Tでサブセグメントを反転する約束があると仮定します。 実際に開始するには、次の手順を実行します。

•現在の頂点で約束をします。

  T.Reversed = false; 

•左と右の息子を交換します。

  temp = T.Left;
   T.Left = T.Right;
   T.Right = temp; 

•約束を後世に変える。 注：trueに設定しないでください（このビットがこれまでに子孫にあったかどうかはわかりません！）が、変更してください。 これには操作^が使用されます。

  T.Left.Reversed ^ = true;
   T.Right.Reversed ^ = true; 

実際、「アレイを実際にフリップ」とは何ですか？ この配列の2つの部分（サブツリー）を実際に交換し、将来これらの2つのサブ配列を反転することを約束します。 すべての約束が最後まで満たされると、元の配列の要素が反転することが簡単にわかります。



注-通常のデカルトツリーでは、検索ツリーのプロパティに違反するため、このような詐欺は実行できません-右のサブツリーのキーは左のキーよりも小さくなります。 ただし、暗黙のデカルトツリーにはキーがまったくなく、インデックスの場合は常にプロパティが尊重されるため、ツリーで壊れることはありません。



セグメントを回すユーザー定義関数は、他の操作と同様に不変の原理で機能します。目的のセグメントを切り取り、ルートにプロミスを設定し、セグメントを貼り付けます。 プッシュおよびフリップ機能のソースコードは次のとおりです。

 public bool Reversed; public static void Push(ImplicitTreap treap) { if (treap == null) return; //    -   if (!treap.Reversed) return; var temp = treap.Left; treap.Left = treap.Right; treap.Right = temp; treap.Reversed = false; if (treap.Left != null) treap.Left.Reversed ^= true; if (treap.Right != null) treap.Right.Reversed ^= true; } public ImplicitTreap Reverse(int A, int B) { ImplicitTreap l, m, r; this.Split(A, out l, out r); r.Split(B - A, out m, out r); m.Reversed ^= true; return Merge(Merge(l, m), r); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

今、あなたは完全に新しい方法で古典的なインタビューのタスクを解決できます:)

ループ配列

フォーカス＃6：循環シフト。 この操作の本質は、知らない人にとっては、図で説明する方が簡単です。







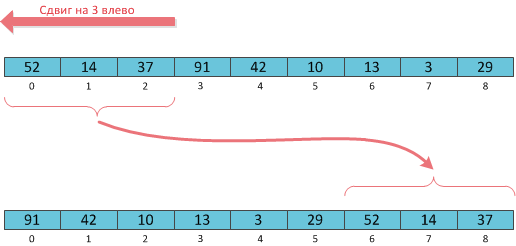
もちろん、巡回シフトは常にO（N）で実行できますが、配列を暗黙的なデカルトツリーとして実装することにより、O（log ₂ N）でシフトできます。 Kだけ左にシフトする手順は簡単です。インデックスKでツリーを切り、逆の順序で貼り付けます。 右へのシフトは対称的で、 NKインデックスでカットする必要があるだけです。

 public ImplicitTreap ShiftLeft(int K) { ImplicitTreap l, r; this.Split(K, out l, out r); return Merge(r, l); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

繰り返しますが、通常のデカルトツリーであるかどうかにかかわらず、2つのSplit結果を接着することは受け入れられないため、暗黙のキーによる操作はデカルトツリーに対して一意です。結局、Mergeは順序付けられたツリーを私たちから期待し、間違った順序で引数をフィードします。

まとめ

暗黙的なキーによるデカルトツリーは、ツリー形式の配列の単純な表現です。これにより、対数時間でそのサブ配列を使用して一連の操作を実行できます。 同時に、O（N）はまだメモリを浪費しています。 もちろん、O表記を使用して、私は少し心を曲がりました。実際の生活では、ツリーが占める実際の記憶が重要であり、デカルトツリーはそのオーバーヘッドで有名だからです。 自分の判断：情報のN、優先度のN、子孫へのリンクの2N、サブツリーのサイズのN-これは生活賃金です。複数のリクエストを追加すると、操作ごとに別のNが得られます。 情報から優先順位を作成することで、あなたの人生を少し改善することができますが、これは、第一に、海の低下（マイナスN）であり、第二に、セキュリティの観点から結果に満ちています：誰かが作成する機能を見つけた場合優先順位を設定すると、デカルトツリーのバランスを大幅に崩すために、悪意のある方法で新しいレコードを作成できる可能性があります。 最終的に、すべてのデータが著しく遅くなる状況が発生する可能性があります-もちろん、そのような場合は読み取られ、顕著な作業が必要です。 ツリーの異なる頂点に異なる素数Pを使用することで危険を取り除くことができます...しかし、これは別の科学的研究のトピックです。 個人的には、デカルトツリーの機能とそのコードの単純さは、高いメモリ消費の問題を超える利点です。 もちろん、プログラムはプログラムによって異なりますが。



興味深い事実から：西洋の文学、記事、インターネットでは、暗黙のキーによるデカルトのツリーについての単一の言及を見つけることができませんでした。 もちろん、英語の用語で何と呼ばれるべきかは誰にもわかりませんが、フォーラムやStackOverflowでの質問も何にもつながりませんでした。 ロシアのスポーツプログラミングACM ICPCの実践において、この構造は2000年に初めて使用され、国際競技大会の多数の勝者である子猫コンピューティングチームのニコライデュロフのメンバーによって発明されました（ただし、Runetは彼の兄弟Pavelを知っています）。



デカルトの木に関する義務的なプログラムは、私が終わるところです。 ほとんどの場合、少なくとも1つまたは2つの部分があります-ツリー操作の代替実装、およびその機能実装について-ただし、原則としてすでに記述されている3つは、人生でデラミドを完全に使用するのに十分な弾薬を構成します。 このチュートリアルの行を通して正直に私と格闘したすべての人に感謝します:)あなたが興味を持っていたことを願っています。