「Hello world！」遺伝的アルゴリズムを使用

最近では、遺伝的アルゴリズムの人気が高まっています。 これらは、さまざまな問題を解決するために使用されます。 どこかで彼らは他の人よりも効率的に働き、どこかでプログラマーが自慢した...



それでは、遺伝的アルゴリズムとは何ですか？ ウィキペディアによると、遺伝的アルゴリズムは、生物学的進化を連想させるメカニズムを使用して、目的のパラメーターをランダムに選択、組み合わせ、変更することにより、最適化とモデリングの問題を解決するために使用されるヒューリスティック検索アルゴリズムです。 これは進化的計算の一種です。 遺伝的アルゴリズムの特徴は、候補生物の組換えの操作を実行する「交配」演算子の使用に重点を置いていることであり、その役割は野生生物における交配の役割に似ています。



つまり 遺伝的アルゴリズムは進化のように機能します。 最初に最初の母集団が作成され、次にそれらが交配されます（突然変異は可能です）。 自然selectionの過程で生き残った個体群は、指定された基準への準拠をテストされます。 彼らが満足していれば、誰もが幸せです。そうでなければ、最後の勝利まで彼らは再び交差します。



それがどのように見えるかは、次の図で見ることができます。









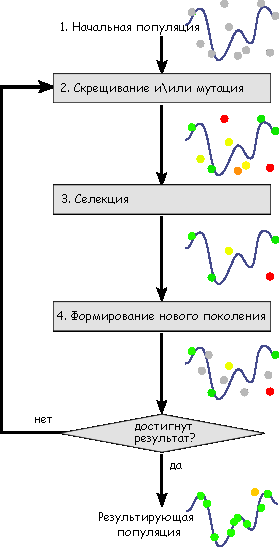
例として、文字列「Hello world！」を作成するアルゴリズムを示します



この遺伝的アルゴリズムには次のパラメーターがあります。

人口規模：	2048
突然変異（％）：	25
エリート（％）：	10

ソースコード

 #include <iostream> // coutなどに
 #include <vector> //ベクトルクラスの場合
 #include <string> //文字列クラス用
 #include <algorithm> //ソートアルゴリズム用
 #include <time.h> //ランダム変数用
 #include <math.h> // abs（）の場合

 #define GA_POPSIZE 2048 //母集団のサイズ
 #define GA_MAXITER 16384 //最大反復回数
 #define GA_ELITRATE 0.10f // Elitism
 #define GA_MUTATIONRATE 0.25f //突然変異
 #define GA_MUTATION RAND_MAX * GA_MUTATIONRATE
 #define GA_TARGET std :: string（ "Hello world！"）

名前空間stdを使用します。				

 struct ga_struct 
 {
	文字列str;  //文字列
	符号なしintフィットネス。  //適合性
 };

 typedef vector <ga_struct> ga_vector;  //略して

 void init_population（ga_vector＆母集団、
					  ga_vector＆buffer） 
 {
	 int tsize = GA_TARGET.size（）;

	 for（int i = 0; i <GA_POPSIZE; i ++）{
		 ga_struct citizen;
		
		 citizen.fitness = 0;
		 citizen.str.erase（）;

		 for（int j = 0; j <tsize; j ++）
			 citizen.str + =（rand（）％90）+ 32;

		ポピュレーション.push_back（市民）;
	 }

	 buffer.resize（GA_POPSIZE）;
 }

 void calc_fitness（ga_vectorおよび人口）
 {
	文字列ターゲット= GA_TARGET;
	 int tsize = target.size（）;
	符号なしintフィットネス。

	 for（int i = 0; i <GA_POPSIZE; i ++）{
		フィットネス= 0;
		 for（int j = 0; j <tsize; j ++）{
			フィットネス+ = abs（int（population [i] .str [j]-target [j]））;
		 }
		
		母集団[i] .fitness =フィットネス。
	 }
 }

 bool fitness_sort（ga_struct x、ga_struct y） 
 {return（x.fitness <y.fitness）;  }

インラインvoid sort_by_fitness（ga_vectorと人口）
 {sort（population.begin（）、population.end（）、fitness_sort）;  }

ボイドエリート主義（ga_vectorと人口、 
				 ga_vector＆buffer、int esize）
 {
	 for（int i = 0; i <esize; i ++）{
		バッファー[i] .str =母集団[i] .str;
		バッファ[i] .fitness =母集団[i] .fitness;
	 }
 }

 void mutate（ga_struct＆メンバー）
 {
	 int tsize = GA_TARGET.size（）;
	 int ipos = rand（）％tsize;
	 int delta =（rand（）％90）+ 32; 

	 member.str [ipos] =（（member.str [ipos] + delta）％122）;
 }

ボイドメイト（ga_vectorと人口、ga_vectorとバッファ）
 {
	 int esize = GA_POPSIZE * GA_ELITRATE;
	 int tsize = GA_TARGET.size（）、spos、i1、i2;

	エリート主義（人口、バッファー、サイズ変更）;

	 //残りをメイト
	 for（int i = esize; i <GA_POPSIZE; i ++）{
		 i1 = rand（）％（GA_POPSIZE / 2）;
		 i2 = rand（）％（GA_POPSIZE / 2）;
		 spos = rand（）％tsize;

		バッファー[i] .str =母集団[i1] .str.substr（0、spos）+ 
			            母集団[i2] .str.substr（spos、esize-spos）;

		 if（rand（）<GA_MUTATION）mutate（buffer [i]）;
	 }
 }

インラインvoid print_best（ga_vector＆gav）
 {cout << "Best：" << gav [0] .str << "（" << gav [0] .fitness << "）" << endl;  }

インラインボイドスワップ（ga_vector *＆母集団、
				  ga_vector *＆buffer）
 {ga_vector * temp =母集団; 人口=バッファー;  buffer = temp;  }

 int main（）
 {
	 srand（符号なし（時間（NULL）））;

	 ga_vector pop_alpha、pop_beta;
	 ga_vector *母集団、*バッファ。

	 init_population（pop_alpha、pop_beta）;
	母集団=＆pop_alpha;
	バッファ=＆pop_beta;

	 for（int i = 0; i <GA_MAXITER; i ++）{
		 calc_fitness（*母集団）;  //適合性を計算します
		 sort_by_fitness（*母集団）;  //母集団をソートします
		 print_best（*母集団）;  //最適な母集団を印刷します

		 if（（*母集団）[0] .fitness == 0）break;

		 mate（*母集団、*バッファー）;  //交配集団
		スワップ（人口、バッファ）;  //バッファをクリアします
	 }

	 0を返します。
 }

コードについていくつかコメントをしたいだけです。 まず、遺伝的アルゴリズムで固定線のサイズを設定するときにごまかしました。これは目的の線のサイズと同じです。 これは、コードの理解を深めるために行われます。 次に、STLクラスベクトルを使用してデータを保存します。これは、並べ替えを簡素化するために行われます。 最後に、プログラムは2つの配列を使用して母集団を保存します。1つは現在の配列、2つ目は次世代のバッファです。 各世代では、計算を高速化するために、ポイントは最も近い整数に丸められます。



適合性の判断

母集団の適合性を判断する機能を見てみましょう。

void calc_fitness(ga_vector &population)

{

string target = GA_TARGET;

int tsize = target.size();

unsigned int fitness;



for (int i=0; i<GA_POPSIZE; i++) {

fitness = 0;

for (int j=0; j<tsize; j++) {

fitness += abs(int(population[i].str[j] - target[j]));

}



population[i].fitness = fitness;

}

}









原則として、母集団の各メンバーはここで単純にスキャンされ、ターゲットラインのメンバーと比較されます。 シンボル間の差が合計され、累積された量がフィットネス値として使用されます（したがって、小さいほど良い）。



結果

プログラムが実行されると、最適な母集団とその適合性（括弧内の数字）が表示されます。

Best: IQQte=Ygqem# (152)

Best: Crmt`!qrya+6 (148)

Best: 8ufxp+Rigfm* (140)

Best: b`hpf"woljh[ (120)

Best: b`hpf"woljh4 (81)

Best: b`hpf"woljh" (63)

Best: Kdoit!wnsk_! (24)

Best: Kdoit!wnsk_! (24)

Best: Idoit!wnsk_! (22)

Best: Idoit!wnsk_! (22)

Best: Idoit!wnsk_! (22)

Best: Idoit!wnsk_! (22)

Best: Ifknm!vkrlf? (17)

Best: Ifknm!vkrlf? (17)

Best: Gfnio!wnskd$ (14)

Best: Ffnjo!wnskd$ (14)

Best: Hflio!wnskd$ (11)

Best: Hflio!wnskd$ (11)

Best: Kflkn wosld" (8)

Best: Ifmmo workd" (6)

Best: Hfljo wosld" (5)

Best: Hflmo workd" (4)

Best: Hflmo workd" (4)

Best: Hflmo workd" (4)

Best: Iflmo world! (3)

Best: Iflmo world! (3)

Best: Hflmo world! (2)

Best: Hflmo world! (2)

Best: Hflko world! (2)

Best: Hflko world! (2)

Best: Hdllo world! (1)

Best: Hfllo world! (1)

Best: Hfllo world! (1)

Best: Helko world! (1)

Best: Hfllo world! (1)

Best: Hfllo world! (1)

Best: Hfllo world! (1)

Best: Hello world! (0)









おわりに

この小さなプログラムが、単純な遺伝的アルゴリズムを使用して問題を解決する方法を実証できることを願っています。 このアルゴリズムは最も効率的ではありませんが、STLを使用すると少し助けになるはずです。 アルゴリズムはVisual Studioでテストされています。



応用例

ある範囲のパラメーターで取引ロボットをテストするには、サイクルで（すべてのプログラムで）範囲ではなく、遺伝的アルゴリズムを使用して範囲を「通過」できます。 そして、時間は9〜12倍に短縮されます。 ＃



英語のオリジナル記事。

遺伝的アルゴリズムとは何ですか？