トポロジカルソート
トポロジカルソート (トポロジカルソート)-グラフの主要なアルゴリズムの1つで、より複雑な問題を解決するために使用されます。
グラフのトポロジカルソートのタスクは次のとおりです。任意のエッジが小さい番号の頂点から大きい番号の頂点につながるように、頂点での線形順序を示します。 明らかに、グラフにサイクルがある場合、この順序は存在しません。
指向ネットワーク (または単にネットワーク)は、アウトラインのない指向グラフと呼ばれます。 この種のタスクでは、有限ネットワークのみが考慮されます。
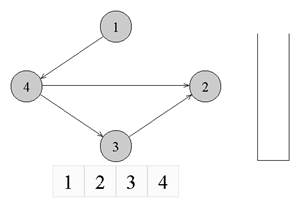
図から、グラフはソートされていないことがわかります。これは、番号4の頂点からのエッジが、番号の小さい頂点( 2 )につながるためです。
トポロジカルソートにはいくつかの方法があります-最も有名なものから:
深さ優先検索または深さ優先検索 (略してDFS )は、グラフトラバーサル方式の1つです。 検索アルゴリズムの説明は次のとおりです。渡されていない各頂点について、渡されていないすべての隣接する頂点を見つけて、それらの検索を繰り返す必要があります。
検索の詳細については、 Habréの記事をご覧ください 。
深さのトラバースを開始し、頂点が処理されると、スタックにプッシュします。 ツアーの終わりに、山は深くスタックから取り出されます。 新しい番号は、スタックからプルする順序で割り当てられます。
色:深度ウォークでは3色が使用されます。 最初は、すべてのピークが白です。 上部が見つかったら、灰色に塗ります。 隣接するすべてのピークのリストが表示されたら、黒で塗りつぶします。
例を使用してこのアルゴリズムを検討する方が簡単だと思います:

↑輪郭なしのグラフがあります。 最初は、すべての頂点が白で、スタックは空です。 一番上の1から詳細にウォークを始めましょう。
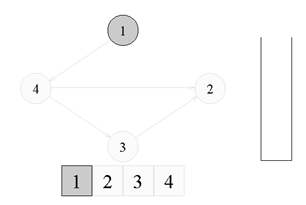
↑一番上の1に進みます。グレーでペイントします。
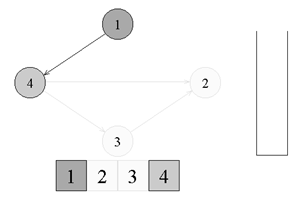
↑頂点番号1から頂点番号4までのエッジがあります。頂点番号4に移動してグレーにペイントします。
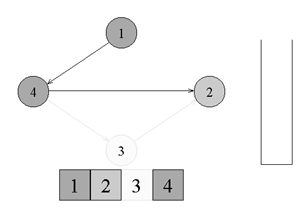
↑頂点番号4から頂点番号2へのエッジがあります。頂点番号2に移動して、灰色にペイントします。

↑頂点番号2から、黒の頂点に移動しないエッジはありません。 頂点番号4に戻ります。頂点番号2を黒で塗り、スタックに配置します。
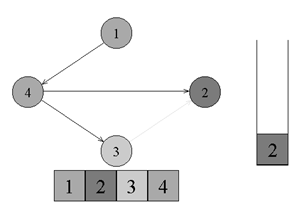
↑頂点番号4から頂点番号3までのエッジがあります。頂点番号3に移動してグレーにペイントします。
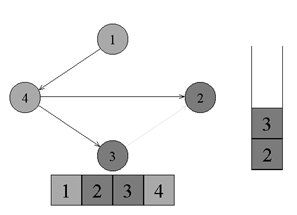
↑頂点番号3から、黒いピークに行かないエッジはありません。 頂点番号4に戻ります。頂点番号3を黒く塗り、スタックに配置します。
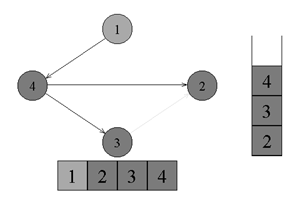
↑頂点番号4から、黒いピークに行かないエッジはありません。 頂点番号1に戻ります。頂点番号4を黒で塗り、スタックに配置します。
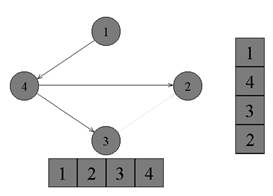
↑頂点番号1から、黒い頂点に移動しないエッジはありません。 それを黒く塗り、スタックに置きます。 ポイントの横断が完了しました。
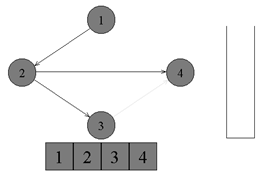
↑次に、スタックからすべての頂点を取得し、それぞれ番号1、2、3、4を割り当てます。 トポロジカルソートアルゴリズムが完成しました。 カウントがソートされます。
トポロジカルソートはさまざまな状況で使用されます。たとえば、アルゴリズムの並列化など、アルゴリズムの説明に従って、操作の依存関係グラフを作成し、トポロジカルにソートし、どの操作が独立しており、同時に実行できるかを決定する必要がある場合です。 トポロジカルソートの使用例は、ツリーのようなパーティションシステムが行われるサイトマップの作成です。 (興味がある場合-Googleへ)
実装について- ここでは、このアルゴリズムを実装する22行のコードを見つけることができます(すべてが慎重にコメント化されています)
グラフのトポロジカルソートのタスクは次のとおりです。任意のエッジが小さい番号の頂点から大きい番号の頂点につながるように、頂点での線形順序を示します。 明らかに、グラフにサイクルがある場合、この順序は存在しません。
指向ネットワーク (または単にネットワーク)は、アウトラインのない指向グラフと呼ばれます。 この種のタスクでは、有限ネットワークのみが考慮されます。

↑トポロジカルソートが適用可能な、方向付けられたソートされていないグラフの例
図から、グラフはソートされていないことがわかります。これは、番号4の頂点からのエッジが、番号の小さい頂点( 2 )につながるためです。
トポロジカルソートにはいくつかの方法があります-最も有名なものから:
- デムクロンのアルゴリズム
- グラフを複数のレベルとして表すためのソート方法
- 深度トラバーサルを使用したトポロジカルソート方法
アルゴリズムの本質
深さ優先検索または深さ優先検索 (略してDFS )は、グラフトラバーサル方式の1つです。 検索アルゴリズムの説明は次のとおりです。渡されていない各頂点について、渡されていないすべての隣接する頂点を見つけて、それらの検索を繰り返す必要があります。
検索の詳細については、 Habréの記事をご覧ください 。
深さのトラバースを開始し、頂点が処理されると、スタックにプッシュします。 ツアーの終わりに、山は深くスタックから取り出されます。 新しい番号は、スタックからプルする順序で割り当てられます。
色:深度ウォークでは3色が使用されます。 最初は、すべてのピークが白です。 上部が見つかったら、灰色に塗ります。 隣接するすべてのピークのリストが表示されたら、黒で塗りつぶします。
例を使用してこのアルゴリズムを検討する方が簡単だと思います:

↑輪郭なしのグラフがあります。 最初は、すべての頂点が白で、スタックは空です。 一番上の1から詳細にウォークを始めましょう。

↑一番上の1に進みます。グレーでペイントします。

↑頂点番号1から頂点番号4までのエッジがあります。頂点番号4に移動してグレーにペイントします。

↑頂点番号4から頂点番号2へのエッジがあります。頂点番号2に移動して、灰色にペイントします。

↑頂点番号2から、黒の頂点に移動しないエッジはありません。 頂点番号4に戻ります。頂点番号2を黒で塗り、スタックに配置します。

↑頂点番号4から頂点番号3までのエッジがあります。頂点番号3に移動してグレーにペイントします。

↑頂点番号3から、黒いピークに行かないエッジはありません。 頂点番号4に戻ります。頂点番号3を黒く塗り、スタックに配置します。

↑頂点番号4から、黒いピークに行かないエッジはありません。 頂点番号1に戻ります。頂点番号4を黒で塗り、スタックに配置します。

↑頂点番号1から、黒い頂点に移動しないエッジはありません。 それを黒く塗り、スタックに置きます。 ポイントの横断が完了しました。

↑次に、スタックからすべての頂点を取得し、それぞれ番号1、2、3、4を割り当てます。 トポロジカルソートアルゴリズムが完成しました。 カウントがソートされます。
申込み
トポロジカルソートはさまざまな状況で使用されます。たとえば、アルゴリズムの並列化など、アルゴリズムの説明に従って、操作の依存関係グラフを作成し、トポロジカルにソートし、どの操作が独立しており、同時に実行できるかを決定する必要がある場合です。 トポロジカルソートの使用例は、ツリーのようなパーティションシステムが行われるサイトマップの作成です。 (興味がある場合-Googleへ)
実装について- ここでは、このアルゴリズムを実装する22行のコードを見つけることができます(すべてが慎重にコメント化されています)
All Articles