MQVプロトコル-古き良きDiffie-Hellmanですが、完全ではありません
30年以上にわたり、Diffie-Hellman鍵配布プロトコルは、そのシンプルさと信頼性を備えた単純な暗号マニアの目に喜ばれてきました。 暗号プロトコルを勉強するよりももっと楽しく勉強するために過去30年を費やした人のために、私は説明します。
Diffie-Hellmanプロトコルは1976年に公開され、非対称暗号化の時代の始まりを示しました。 その本質は見事に単純です。アリスとボブは対称暗号システムの共通鍵を取得したいと考えています。 これを行うには、2つの大きな数字gとpを選択して同意しました。 これらの番号は両方に知られており、それらを秘密にしておくことは意味がありません。 その後、アリスは密かに大きな秘密番号aを生成し、ボブ-大きい番号bを生成します。 そして、単純な算術が取り上げられます。 アリスはボブに番号を送信します
 。
。
ボブは次に、アリスを送ります
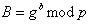 。
。
次に、共有キーを取得するために、アリスは計算します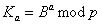 ボブは見つける
ボブは見つける 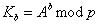 。
。
それを確認するのは簡単です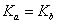 なぜなら
なぜなら
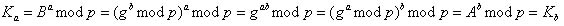 。
。
このアイデアの天才は、アリスとボブがキーKを取得するのにそれほど時間はかからないことですが、攻撃者はKを見つけるために離散対数問題を解決できる必要があります。
読者によく知られている事実を退屈させることを恐れて、私はその点に右に曲がります。 しかし、理論から離れて実践に移るとどうなりますか? 次に、以下を取得します。
Diffie-Hellmanプロトコルは、受動的な攻撃に完全に抵抗しますが、中間者攻撃が実装されている場合、それは耐えられません。 実際、プロトコルでは、アリスもボブも対談者が誰であるかを確実に判断することはできないため、ボブとアリスがボブにアリスであるふりをするメロリーとの関係を確立し、ボブがアリスを表すという次の状況を想像することは十分に可能です。 そして、Diffie-Hellmanプロトコルの代わりに、次のようなものが得られます。
つまり、Melloryは、Alice(これはBobであると考えている)と共有する1つのキーと、Bob(これはAliceと考えている)と共有する1つのキーを取得します。 そして、したがって、彼はアリスからボブがキーでそれを解読するためのメッセージを受け取ることができます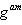 、読み取り、キーで暗号化
、読み取り、キーで暗号化 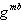 それをボブに渡します。 したがって、偽造は非常に長い間気付かれることはありません。
それをボブに渡します。 したがって、偽造は非常に長い間気付かれることはありません。
このような脆弱性に対処する方法は? 最も論理的でシンプルな答え:相互認証が必要です。 そして、ここでEDSが助けになります。
ボブがアリスの公開鍵を持ち、これが本当にアリスの鍵であることを100%確信している場合、攻撃の途中でアリスを保護するには、アリスがステップ1で自分の秘密鍵で番号に署名するだけで十分です。アリスのために、しかし彼は彼女の署名を偽造することができず、「あいまいな疑い」はすぐにボブを苦しめ始めます。
解決策が見つかり、プロトコルが完成し、脆弱性が修正されたようです。 しかし...いつものように、1つがあります。 この場合、そのような役割は、署名を追加することによるメッセージのサイズの過度の増加です。 次の表は、この効果を明確に示しています。
この表からわかるように、メッセージのサイズは大幅に増加します。 どうやら、神はこれらの余分な320ビットで彼らと一緒にいるでしょう。 しかし、暗号化は半分の測定値を許容しません。 これがMQVプロトコルが発明された理由で、Diffie-Hellmanの脆弱性を緩和すると同時に、EDSを使用していません。
したがって、MQVプロトコルは、当事者の相互認証をサポートするキー配布プロトコルであり、これにより、従来のDiffie-Hellmanに固有の「中間者」攻撃に対する脆弱性を排除します。 特に、デジタル署名などの補助情報はユーザーの認証に使用されないため、送信されるメッセージのサイズを大幅に削減できます。
次に、プロトコル自体について説明します。
アリスとボブにはそれぞれ公開鍵と秘密鍵で構成される独自の鍵ペアがあります。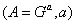 そして
そして  。 もちろん、ボブはアリスの公開鍵を知っていて、それが次にボブの公開鍵を知っています。
。 もちろん、ボブはアリスの公開鍵を知っていて、それが次にボブの公開鍵を知っています。
次に、アリスとボブはセッションキーペアを生成します。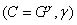 そして
そして 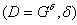 。
。
次に、古典的なDiffie-Hellmanプロトコルのような交換があります。
アリスとボブ: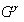
ボブとアリス: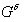
アリスは今、知っている:A、B、C、D、 a 、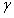 。
。
そしてボブは知っている:A、B、C、D、 b 、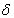 。
。
共通キーKを取得するには、次の操作を実行する必要があります。
アリス:
2で割ったビット単位のメッセージサイズに等しい数値lを選択します。したがって、EC-MQVが使用され、メッセージ長が160ビットの場合、l = 80です。
1.セット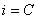
2.検索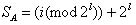
3.セット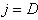
4.計算する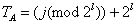
5.検索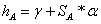
6.計算する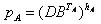
ボブも同じことをしますが、秘密鍵を使用します。
1.セット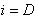
2.検索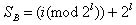
3.セット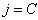
4.計算する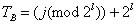
5.検索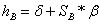
6.計算する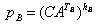
結果の数値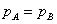 共有秘密鍵があります。 これを確認してください:
共有秘密鍵があります。 これを確認してください:
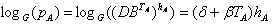 なぜなら
なぜなら 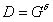 そして
そして 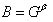 ;
;
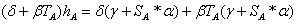 なぜなら
なぜなら 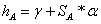 ;
;
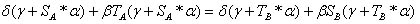 なぜなら
なぜなら 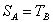 そして
そして 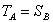 ;
;
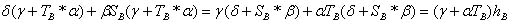 なぜなら
なぜなら 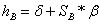 ;
;
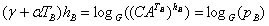 。
。
変換では、アリスとボブの両方の秘密鍵が使用されることに注意してください。 つまり プロトコルのすべてのユーザーは、接続を確立する相手に加えて、誰も共通鍵を取得できないことを確信できます。
見かけの複雑さにも関わらず、MQVプロトコルは、EDSを使用した回路と比較して速度を失うことはありません。 プロトコルを使用する利点は次のとおりです。 これは、第一に「中間者」攻撃への抵抗であり、第二にメッセージのサイズが小さく、第三にプロトコルの便利な実装であり、ユーザーが各送信メッセージに署名する必要がなくなります。
upd:
文学
1. N.スマート「暗号化」(私が出会ったロシア語でのMQVプロトコルの最も完全な説明)。
2. Bolotov A. et al。「楕円暗号の基本的な導入」(楕円曲線のプロトコル記述)。
3.さて、 ウィキペディアへのリンク。
Diffie-Hellmanプロトコルは1976年に公開され、非対称暗号化の時代の始まりを示しました。 その本質は見事に単純です。アリスとボブは対称暗号システムの共通鍵を取得したいと考えています。 これを行うには、2つの大きな数字gとpを選択して同意しました。 これらの番号は両方に知られており、それらを秘密にしておくことは意味がありません。 その後、アリスは密かに大きな秘密番号aを生成し、ボブ-大きい番号bを生成します。 そして、単純な算術が取り上げられます。 アリスはボブに番号を送信します
 。
。
ボブは次に、アリスを送ります
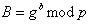 。
。
次に、共有キーを取得するために、アリスは計算します
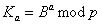 ボブは見つける
ボブは見つける 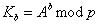 。
。
それを確認するのは簡単です
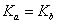 なぜなら
なぜなら
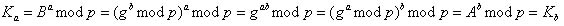 。
。
このアイデアの天才は、アリスとボブがキーKを取得するのにそれほど時間はかからないことですが、攻撃者はKを見つけるために離散対数問題を解決できる必要があります。
読者によく知られている事実を退屈させることを恐れて、私はその点に右に曲がります。 しかし、理論から離れて実践に移るとどうなりますか? 次に、以下を取得します。
Diffie-Hellmanプロトコルは、受動的な攻撃に完全に抵抗しますが、中間者攻撃が実装されている場合、それは耐えられません。 実際、プロトコルでは、アリスもボブも対談者が誰であるかを確実に判断することはできないため、ボブとアリスがボブにアリスであるふりをするメロリーとの関係を確立し、ボブがアリスを表すという次の状況を想像することは十分に可能です。 そして、Diffie-Hellmanプロトコルの代わりに、次のようなものが得られます。
| ステップ
| アリス
| メロリー
| ボブ
|
| 1
| 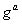 
| 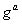
| |
| 2
| 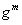 
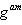
| 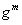
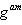
| |
| 3
| 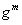 
| 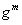
| |
| 4
| 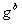 
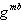
| 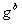
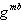
|
つまり、Melloryは、Alice(これはBobであると考えている)と共有する1つのキーと、Bob(これはAliceと考えている)と共有する1つのキーを取得します。 そして、したがって、彼はアリスからボブがキーでそれを解読するためのメッセージを受け取ることができます
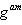 、読み取り、キーで暗号化
、読み取り、キーで暗号化 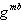 それをボブに渡します。 したがって、偽造は非常に長い間気付かれることはありません。
それをボブに渡します。 したがって、偽造は非常に長い間気付かれることはありません。
防衛としてのEDS
このような脆弱性に対処する方法は? 最も論理的でシンプルな答え:相互認証が必要です。 そして、ここでEDSが助けになります。
ボブがアリスの公開鍵を持ち、これが本当にアリスの鍵であることを100%確信している場合、攻撃の途中でアリスを保護するには、アリスがステップ1で自分の秘密鍵で番号に署名するだけで十分です。アリスのために、しかし彼は彼女の署名を偽造することができず、「あいまいな疑い」はすぐにボブを苦しめ始めます。
解決策が見つかり、プロトコルが完成し、脆弱性が修正されたようです。 しかし...いつものように、1つがあります。 この場合、そのような役割は、署名を追加することによるメッセージのサイズの過度の増加です。 次の表は、この効果を明確に示しています。
| アルゴリズム
| メッセージサイズ
| 署名サイズ
| 総サイズ
|
| Diffie-Hellman + DSA署名
| 1024ビット
| 320ビット
| 1344ビット
|
| Diffie-Hellman + RSA署名
| 1024
| 1024
| 2048
|
| Diffie-Hellman(楕円曲線上)+ RSA署名
| 160
| 1024
| 1184
|
| Diffie-Hellman(楕円曲線上)+ DSA署名(楕円曲線上)
| 160
| 320
| 480
|
この表からわかるように、メッセージのサイズは大幅に増加します。 どうやら、神はこれらの余分な320ビットで彼らと一緒にいるでしょう。 しかし、暗号化は半分の測定値を許容しません。 これがMQVプロトコルが発明された理由で、Diffie-Hellmanの脆弱性を緩和すると同時に、EDSを使用していません。
MQVプロトコル
したがって、MQVプロトコルは、当事者の相互認証をサポートするキー配布プロトコルであり、これにより、従来のDiffie-Hellmanに固有の「中間者」攻撃に対する脆弱性を排除します。 特に、デジタル署名などの補助情報はユーザーの認証に使用されないため、送信されるメッセージのサイズを大幅に削減できます。
| プロトコル
| メッセージサイズ
|
| Mqv
| 1024ビット
|
| MQV(楕円曲線上)
| 160ビット
|
次に、プロトコル自体について説明します。
アリスとボブにはそれぞれ公開鍵と秘密鍵で構成される独自の鍵ペアがあります。
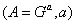 そして
そして  。 もちろん、ボブはアリスの公開鍵を知っていて、それが次にボブの公開鍵を知っています。
。 もちろん、ボブはアリスの公開鍵を知っていて、それが次にボブの公開鍵を知っています。
次に、アリスとボブはセッションキーペアを生成します。
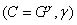 そして
そして 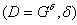 。
。
次に、古典的なDiffie-Hellmanプロトコルのような交換があります。
アリスとボブ:
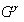
ボブとアリス:
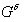
アリスは今、知っている:A、B、C、D、 a 、
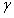 。
。
そしてボブは知っている:A、B、C、D、 b 、
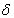 。
。
共通キーKを取得するには、次の操作を実行する必要があります。
アリス:
2で割ったビット単位のメッセージサイズに等しい数値lを選択します。したがって、EC-MQVが使用され、メッセージ長が160ビットの場合、l = 80です。
1.セット
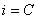
2.検索
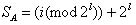
3.セット
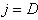
4.計算する
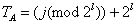
5.検索
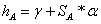
6.計算する
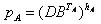
ボブも同じことをしますが、秘密鍵を使用します。
1.セット
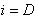
2.検索
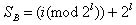
3.セット
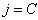
4.計算する
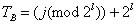
5.検索
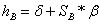
6.計算する
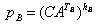
結果の数値
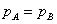 共有秘密鍵があります。 これを確認してください:
共有秘密鍵があります。 これを確認してください:
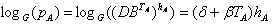 なぜなら
なぜなら 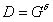 そして
そして 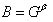 ;
;
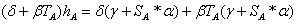 なぜなら
なぜなら 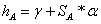 ;
;
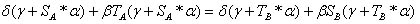 なぜなら
なぜなら 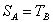 そして
そして 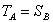 ;
;
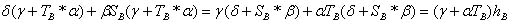 なぜなら
なぜなら 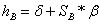 ;
;
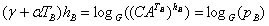 。
。
変換では、アリスとボブの両方の秘密鍵が使用されることに注意してください。 つまり プロトコルのすべてのユーザーは、接続を確立する相手に加えて、誰も共通鍵を取得できないことを確信できます。
見かけの複雑さにも関わらず、MQVプロトコルは、EDSを使用した回路と比較して速度を失うことはありません。 プロトコルを使用する利点は次のとおりです。 これは、第一に「中間者」攻撃への抵抗であり、第二にメッセージのサイズが小さく、第三にプロトコルの便利な実装であり、ユーザーが各送信メッセージに署名する必要がなくなります。
upd:
文学
1. N.スマート「暗号化」(私が出会ったロシア語でのMQVプロトコルの最も完全な説明)。
2. Bolotov A. et al。「楕円暗号の基本的な導入」(楕円曲線のプロトコル記述)。
3.さて、 ウィキペディアへのリンク。
All Articles