परिचय
करुणा की एक जोड़ी द्वारा एक मनमाना कोण और एक शासक के बिना विभाजन के त्रिशूल का प्रसिद्ध कार्य सबसे पुरानी समस्याओं में से एक है जो कई सहस्राब्दी के लिए कई गणितज्ञों को आकर्षित करता है। समस्या की अस्थिरता, अर्थात्। इस तरह के निर्माण की असंभवता अंततः 19 वीं शताब्दी में साबित हुई थी, हालांकि, कुछ लोग अभी भी अपने समाधान की पेशकश करते हैं। उदाहरण के लिए, रूसी विज्ञान अकादमी के एक शिक्षाविद का निर्णय विज्ञान और जीवन पत्रिका में प्रकाशित हुआ था। हालांकि, शायद यह इस तरह के एक नाजुक ट्रोलिंग है ...

विज्ञान और जीवन, नंबर 3, 1998
यह सच है कि गणित के एक प्रोफेसर के अनुसार, कोण की त्रिज्या के समाधान के साथ अक्षरों का प्रवाह और फ़र्मेट के महान प्रमेय के सरल प्रमाण हाल ही में स्पष्ट रूप से कम हो गए हैं। अब वे उसे, एक नियम के रूप में, रीमान की परिकल्पना का सबूत भेजते हैं ।
खेतों
वास्तव में, एक क्षेत्र शून्य के साथ तत्वों का एक समूह है जो आपस में जोड़ा जा सकता है, घटाया जा सकता है, गुणा और भाग कर सकता है (विभाजन को छोड़कर), और इस तरह के संचालन का परिणाम हमेशा विशिष्ट रूप से निर्धारित होता है और इस क्षेत्र का एक तत्व भी है। इसके अलावा, वास्तविक संख्याओं के साथ अंकगणितीय संचालन के लिए, फ़ील्ड में आप परिणाम बदले बिना शर्तों / कारकों और खुले कोष्ठक को इंटरचेंज कर सकते हैं।
वास्तविक संख्या R का सेट किसी क्षेत्र का सबसे सरल उदाहरण है। ऐसी संख्याओं के साथ किसी भी अंकगणितीय संचालन के लिए (शून्य से विभाजन को छोड़कर), परिणाम एक वास्तविक संख्या है। एक समान उदाहरण जटिल संख्या सी का क्षेत्र है।
परिमेय संख्याओं का क्षेत्र Q पूर्णांक m, n के लिए भिन्न m / n का समूह है। यह देखना आसान है कि अंशों को जोड़ने / गुणा / गुणा करने पर, एक अंश प्राप्त होता है, इसलिए क्यू एक क्षेत्र है।
पूर्णांक Z का सेट, इसके विपरीत, एक फ़ील्ड नहीं है, क्योंकि विभाजन हमेशा एक पूर्णांक नहीं देता है: 5/7 गैर-पूर्णांक है, इसलिए यह Z में शामिल नहीं है।
अलग-अलग, अंतिम फ़ील्ड या गैलोज़ फ़ील्ड, तत्वों की एक सीमित संख्या वाले क्षेत्रों पर ध्यान दिया जाना चाहिए। प्राइम पी के लिए, फ़ील्ड F p को p संख्याओं के समूह {0,1, ..., p-1} के रूप में दर्शाया जा सकता है, जिसमें अंकगणितीय संचालन को modulo p किया जाता है। उदाहरण के लिए, फ़ील्ड में F 5 : 2 + 3 = 5 mod 5 = 0। 2 * 3 = 6 मॉड 5 = 1 और इसलिए 1/3 = (2 * 3) / 3 = 2, आदि। परिमित फ़ील्ड अक्सर बीजगणितीय त्रुटि-सुधार कोड और क्रिप्टोग्राफ़ी में उपयोग किए जाते हैं: रीड-सोलोमन कोड, एईएस, और अण्डाकार क्रिप्टोग्राफ़ी परिमित फ़ील्ड पर काम करते हैं।
क्षेत्र का विस्तार
फ़ील्ड L फ़ील्ड K का एक विस्तार है और L / K द्वारा निरूपित किया जाता है यदि L में पूरी तरह से K होता है, और L और K में कार्य पहचान के अनुसार कार्य करते हैं। उदाहरण के लिए, फ़ील्ड R, परिमेय संख्याओं Q के क्षेत्र के R / Q का विस्तार है, और जटिल संख्या C का क्षेत्र R / C का विस्तार है।
एक मनमाना फ़ील्ड K पर विचार करें और K [x] से K. एक बहुपद p (x) के गुणांकों के साथ एक चर x में सभी बहुपदों के सेट K [x] को K [x] से अविभाज्य (गैर-स्थिर) कारकों में से एक क्षेत्र पर irreducible कहा जाता है। उदाहरण के लिए, बहुपद P (x) = x 2 +1 R से अधिक अप्रासंगिक है, लेकिन C के कारण पुनर्वितरण होता है, क्योंकि C [x] से गुणनखंडन: x 2 + 1 = (xi) (x + i)।
हम फ़ील्ड K के ऐसे एक्सटेंशन L / K में रूचि लेंगे, जिसका निर्माण K को कुछ एलिमेंट w (L में शामिल है, लेकिन K में नहीं) और W से और K से तत्वों के साथ सभी संभावित भावों के साथ किया जाएगा। तब हम फील्ड के विस्तार को निरूपित करेंगे: एल / के = के (डब्ल्यू)। यदि तत्व W, K [x] (अर्थात, p (w) = 0) से डिग्री d के कुछ इरेड्यूसिएबल बहुपद p (x) का मूल है, तो हम L / K = K (w) = K / x / / लिखते हैं ( p (x)) और कहते हैं कि L, डिग्री का एक विस्तार है [L: K] = d , और w में फ़ील्ड D पर डिग्री D है। इस मामले में, विस्तार L / K को बहुपद के साथ बहुपद के सेट के रूप में दर्शाया जा सकता है K modulo से बहुपद p (x), अर्थात। डिग्री की बहुपद की संख्या d से कम होती है। पहली डिग्री के एक्सटेंशन्स L / K प्रारंभिक फ़ील्ड L = K के बराबर हैं, अर्थात। वास्तव में फ़ील्ड K का विस्तार न करें।
जटिल संख्याओं के क्षेत्र के उदाहरण पर लौटना: C = C / R को एक काल्पनिक इकाई जोड़कर R से प्राप्त किया जा सकता है
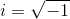 सी / आर = आर (आई); इसके अलावा, मैं बहुपद x 2 +1 (i 2 + 1 = 0 के बाद से) की जड़ है, जो R के ऊपर दूसरी डिग्री है, इसलिए C = C / R = R [x] / (x 2 +1) डिग्री 2 का विस्तार है, और प्रतिनिधित्व योग्य है आर से गुणांकों के साथ पहली और शून्य डिग्री के बहुपद के एक सेट के रूप में, जिसमें संचालन modulo x 2 +1 किया जाता है। या, समकक्ष,
सी / आर = आर (आई); इसके अलावा, मैं बहुपद x 2 +1 (i 2 + 1 = 0 के बाद से) की जड़ है, जो R के ऊपर दूसरी डिग्री है, इसलिए C = C / R = R [x] / (x 2 +1) डिग्री 2 का विस्तार है, और प्रतिनिधित्व योग्य है आर से गुणांकों के साथ पहली और शून्य डिग्री के बहुपद के एक सेट के रूप में, जिसमें संचालन modulo x 2 +1 किया जाता है। या, समकक्ष,  ।
।
वाह। कठिन सिद्धांत खत्म हो गया है, फिर आसान और मजेदार अभ्यास शुरू होता है।
कम्पास और एक शासक
अब हम खुद से पूछते हैं कि कम्पास और शासक की सहायता से क्या संभव है और क्या नहीं बनाया जा सकता है?
इस तरह का कोई भी निर्माण हमें दिए गए विमान पर कुछ दो बिंदुओं से शुरू होता है जो एक इकाई खंड को परिभाषित करते हैं। हम इन बिंदुओं पर विचार करेंगे। दो बिंदुओं के निर्मित होने के बाद, हम या तो उनके माध्यम से एक सीधी रेखा खींच सकते हैं, या उनमें से एक में केंद्रित सर्कल बनाने और दूसरे से गुजरने के लिए कम्पास की एक जोड़ी का उपयोग कर सकते हैं। इन रेखाओं और वृत्तों को निर्माण भी कहा जाएगा। निर्मित लाइनों और हलकों का चौराहा नए निर्मित बिंदु देता है जिसके माध्यम से आप नई रेखाएं और मंडलियां बना सकते हैं, आदि इसके साथ, विभाजन के बिना कम्पास और एक शासक के साथ संचालन समाप्त हो जाता है। यदि वे समान परिचालनों की सीमित संख्या के माध्यम से निर्मित किए जा सकते हैं, तो अंक और रेखाएँ उपलब्ध हैं।
हम कार्टेशियन कोऑर्डिनेट सिस्टम 0xy को पेश करते हैं, जिसमें शुरुआती दो बिंदुओं में निर्देशांक (0,0) और (1,0) हैं। मान लीजिए कि संख्या a, b, c, d, a, b ', c', d 'क्षेत्र K के हैं। यह दिखाया जा सकता है कि इस तरह के निर्देशांक वाले बिंदुओं पर निर्मित रेखाएं किसी क्षेत्र में निर्देशांक वाले बिंदुओं पर प्रतिच्छेद करती हैं जैसे L कि [एल: के] .2।
दिखाने की जरूरत है
अंक (ए, बी), (सी, डी) से गुजरने वाली रेखा समीकरण (एसी) (yb) = (बीडी) (xa) द्वारा दी गई है। (A, b) केंद्र (c, d) से गुजरने वाले वृत्त का समीकरण 2 x (yb) 2 = (ca) 2 + (db) 2 द्वारा दिया जाता है । बिंदुओं (a, b), (c, d), और (a, b '), (c', d ') के दो युग्मों से निर्मित रेखाओं और वृत्तों के समीकरणों के गुणांक भी K में होते हैं। दो ऐसी रेखाओं के प्रतिच्छेदन बिंदु के निर्देशांक हैं एक रैखिक प्रणाली को हल करके
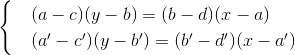
समाधान समीकरणों के गुणांक के कुछ रैखिक कार्यों के संबंधों द्वारा व्यक्त किया जाता है, अर्थात, (x, y) भी K के अंतर्गत आता है। लाइन और सर्कल के बिंदु के निर्देशांक सिस्टम से लिए गए हैं
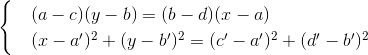
पहले समीकरण से y के माध्यम से एक्स को व्यक्त करना, दूसरे में x को प्रतिस्थापित करना और बाहर करना, हम K से गुणांक के साथ y के लिए एक द्विघात समीकरण प्राप्त करते हैं। समाधान गुणांक और जड़ के रैखिक संयोजन के माध्यम से व्यक्त किया जाता है।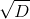 समीकरण के विवेकशील डी से। जड़ अब आवश्यक रूप से K का तत्व नहीं है, बल्कि एक विस्तार तत्व है
समीकरण के विवेकशील डी से। जड़ अब आवश्यक रूप से K का तत्व नहीं है, बल्कि एक विस्तार तत्व है 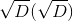 । यदि D, K में पूर्ण वर्ग नहीं है, तो हमारे पास दूसरी डिग्री का विस्तार है, चूंकि
। यदि D, K में पूर्ण वर्ग नहीं है, तो हमारे पास दूसरी डिग्री का विस्तार है, चूंकि 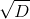 विडंबनापूर्ण बहुपद की जड़ है
विडंबनापूर्ण बहुपद की जड़ है  । एक्स के लिए इसी तरह के तर्क देते हैं
। एक्स के लिए इसी तरह के तर्क देते हैं 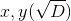 । यदि विवेचक नकारात्मक है, तो समाधान काल्पनिक हैं, सर्कल रेखा के साथ प्रतिच्छेद नहीं करता है, और कोई नया बिंदु नहीं बनता है।
। यदि विवेचक नकारात्मक है, तो समाधान काल्पनिक हैं, सर्कल रेखा के साथ प्रतिच्छेद नहीं करता है, और कोई नया बिंदु नहीं बनता है।
अंत में, दो हलकों के चौराहे के लिए
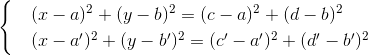
एक समीकरण से दूसरे को घटाएं, x 2 , y 2 को कम करें और x, y में एक समीकरण रैखिक प्राप्त करें। सिस्टम में एक नया समीकरण जोड़ें, और फिर हम एक सीधी रेखा और एक सर्कल के चौराहे के मामले में आते हैं, जिसमें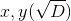 ।
।
हम इन गणनाओं को (a, b) = (0,0), (c, d) = (1,0), (a, b ') = (- 4 / 9,3), (c') के उदाहरण से प्रदर्शित करते हैं। d ') = (1 / 3,1 / 2) Q से निर्देशांक के साथ। दो रेखाओं का अंतर, एक वृत्त के साथ एक सीधी रेखा, इन चार बिंदुओं पर निर्मित दो वृत्त, निर्देशांक होते हैं।
(x 0 , y 0 ) = (22 / 45.0),
(x 1 , y 1 ) =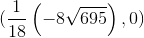 ।
।
(x 2 , y 2 ) =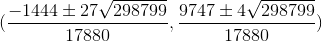 ।
।
क्रमशः। यह देखा जा सकता है कि x 0 , y 0 beQ, रेखा वृत्त के साथ प्रतिच्छेद नहीं करती है, और x 2 , y 2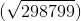 ।
।
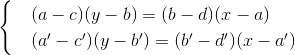
समाधान समीकरणों के गुणांक के कुछ रैखिक कार्यों के संबंधों द्वारा व्यक्त किया जाता है, अर्थात, (x, y) भी K के अंतर्गत आता है। लाइन और सर्कल के बिंदु के निर्देशांक सिस्टम से लिए गए हैं
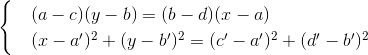
पहले समीकरण से y के माध्यम से एक्स को व्यक्त करना, दूसरे में x को प्रतिस्थापित करना और बाहर करना, हम K से गुणांक के साथ y के लिए एक द्विघात समीकरण प्राप्त करते हैं। समाधान गुणांक और जड़ के रैखिक संयोजन के माध्यम से व्यक्त किया जाता है।
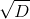 समीकरण के विवेकशील डी से। जड़ अब आवश्यक रूप से K का तत्व नहीं है, बल्कि एक विस्तार तत्व है
समीकरण के विवेकशील डी से। जड़ अब आवश्यक रूप से K का तत्व नहीं है, बल्कि एक विस्तार तत्व है 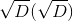 । यदि D, K में पूर्ण वर्ग नहीं है, तो हमारे पास दूसरी डिग्री का विस्तार है, चूंकि
। यदि D, K में पूर्ण वर्ग नहीं है, तो हमारे पास दूसरी डिग्री का विस्तार है, चूंकि 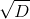 विडंबनापूर्ण बहुपद की जड़ है
विडंबनापूर्ण बहुपद की जड़ है  । एक्स के लिए इसी तरह के तर्क देते हैं
। एक्स के लिए इसी तरह के तर्क देते हैं 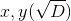 । यदि विवेचक नकारात्मक है, तो समाधान काल्पनिक हैं, सर्कल रेखा के साथ प्रतिच्छेद नहीं करता है, और कोई नया बिंदु नहीं बनता है।
। यदि विवेचक नकारात्मक है, तो समाधान काल्पनिक हैं, सर्कल रेखा के साथ प्रतिच्छेद नहीं करता है, और कोई नया बिंदु नहीं बनता है।
अंत में, दो हलकों के चौराहे के लिए
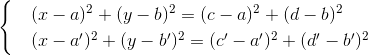
एक समीकरण से दूसरे को घटाएं, x 2 , y 2 को कम करें और x, y में एक समीकरण रैखिक प्राप्त करें। सिस्टम में एक नया समीकरण जोड़ें, और फिर हम एक सीधी रेखा और एक सर्कल के चौराहे के मामले में आते हैं, जिसमें
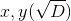 ।
।
हम इन गणनाओं को (a, b) = (0,0), (c, d) = (1,0), (a, b ') = (- 4 / 9,3), (c') के उदाहरण से प्रदर्शित करते हैं। d ') = (1 / 3,1 / 2) Q से निर्देशांक के साथ। दो रेखाओं का अंतर, एक वृत्त के साथ एक सीधी रेखा, इन चार बिंदुओं पर निर्मित दो वृत्त, निर्देशांक होते हैं।
(x 0 , y 0 ) = (22 / 45.0),
(x 1 , y 1 ) =
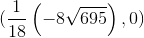 ।
।
(x 2 , y 2 ) =
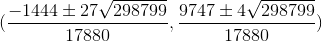 ।
।
क्रमशः। यह देखा जा सकता है कि x 0 , y 0 beQ, रेखा वृत्त के साथ प्रतिच्छेद नहीं करती है, और x 2 , y 2
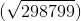 ।
।
इस प्रकार, जब हमारी ड्राइंग में एक नई लाइन जोड़ते हैं, तो नव निर्मित बिंदुओं के निर्देशांक वर्तमान फ़ील्ड K या उसके विस्तार L / K की सीमा में स्थित होते हैं। L / K से बिंदुओं पर एक नया सर्कल बनाते समय, फ़ील्ड L / K का एक विस्तार पहले से ही बनता है: E / एल, [ई: एल] = २। क्रमिक विस्तार की डिग्री गुणा की जाती है, अर्थात, E डिग्री के क्षेत्र के E / K का विस्तार है [E: K] = [E: L] [L: K] = 2 * 2 = 2 2 । इसलिए, सभी पहुंच योग्य बिंदुओं में केवल डिग्री 2 एन के क्षेत्र K के विस्तार से निर्देशांक होते हैं । बिंदु (ए, बी) का निर्माण अंकों (ए, 0), (बी, 0) के निर्माण के बराबर है, इसलिए हम इस प्रकार कहते हैं कि "लंबाई के एक खंड का निर्माण करें" या "संख्या बी का निर्माण करें"।
त्रिदोष कोण

आइए हम बिंदु (0,0) पर कोण ect पर प्रतिच्छेद करते हुए एक जोड़ी रेखाएँ दें। हमारे अन्य शुरुआती बिंदु (1,0) के साथ संयोजन में, एक कोण को परिभाषित करना लंबाई के एक खंड को परिभाषित करने के बराबर है, अर्थात, हम क्षेत्र Q (cos ξ) में संख्याओं के साथ निर्माण शुरू करते हैं। बदले में, कोण, / 3 का निर्माण लंबाई के एक खंड के निर्माण के बराबर है (of / 3)। त्रिकोणमितीय पहचान cos ξ = 4cos 3 (3/3) -3cos (ometric / 3) से पता चलता है कि हमें बहुपद p (x) = 4x 3 -3x-cos ξ के मूल का निर्माण करने की आवश्यकता है (लंबाई c का खंड) निर्देशांक के साथ अंक के साथ शुरू फ़ील्ड Q (cos ξ) में । हालाँकि, लगभग सभी कोणों के लिए, यह बहुपद क्षेत्र Q (cos।) के क्षेत्र में अप्रासंगिक है। उदाहरण के लिए, मामले में 60 = 60 ° cos 1/2 = 1/2, बहुपद p (x) = 4x 3 -3x-1/2 फ़ील्ड Q (cos ξ) = Q (1/2) = Q से अधिक नहीं होता है। चूँकि cos ((/ 3) का विस्तार Q (cos (3/3)) = Q [x] / (p (x) फ़ील्ड Q (cos in) के रूप में होता है, और यह स्थिति irreducible p (x) की डिग्री की है। बहुपद p (x), अर्थात 3 ≠ 2 n , तब cos (ξ / 3) खंड की पहुंच योग्य लंबाई या बिंदु का समन्वय नहीं है। इसलिए, इन मामलों में, कोण की एक सटीक त्रिशूल असंभव है।
बेशक, ऐसे कोण हैं जो त्रिशक्ति की अनुमति देते हैं। उदाहरण के लिए, 30 ° के कोण का निर्माण करना आसान है, () = 90 °) का कोण होना (और नहीं भी)। इस स्थिति में, बहुपद p (x) = 4x 3 -3x-cos, = 4x 3 -3x = x (4x 2 -3) Q (cos ξ) = Q में कारक होता है; 30 ° cos के लिए इरेड्यूसिबल बहुपद 4x 2 -3 है, विस्तार Q (cos () / 3)) = Q (
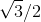 ) के पास Q पर 2 डिग्री है, और इसके तत्व कम्पास और शासक द्वारा आसानी से सुलभ हैं। लेकिन ऐसे अच्छे कोण नगण्य हैं।
) के पास Q पर 2 डिग्री है, और इसके तत्व कम्पास और शासक द्वारा आसानी से सुलभ हैं। लेकिन ऐसे अच्छे कोण नगण्य हैं।
निष्कर्ष
एक कम्पास और एक शासक के साथ अन्य ज्यामितीय निर्माणों की संभावना के प्रमाण में भी इसी तरह के दृष्टिकोण का उपयोग किया जाता है:
- क्यूब को दोगुना करने का कार्य - पुरातनता की एक और अनसुलझी समस्या है - इसमें एक कम्पास और एक शासक के साथ एक क्यूब के किनारों का निर्माण होता है, जिसकी मात्रा किसी दिए गए क्यूब के आयतन से दोगुनी होती है, अर्थात एक लंबाई खंड के निर्माण में
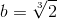 दिए गए एकल खंड के लिए। यह देखना आसान है कि b, बहुपद x 3 -2 का मूल है जो कि Q से अधिक अप्रासंगिक है, Q की डिग्री 3 degree 2 n है , और इसलिए, अप्राप्य है।
दिए गए एकल खंड के लिए। यह देखना आसान है कि b, बहुपद x 3 -2 का मूल है जो कि Q से अधिक अप्रासंगिक है, Q की डिग्री 3 degree 2 n है , और इसलिए, अप्राप्य है।
- एक सर्कल के चतुर्भुज के साथ एक समान स्थिति प्राप्त की जाती है - एक दिए गए सर्कल में क्षेत्र के बराबर एक वर्ग के निर्माण का कार्य। कार्य एक संख्या का निर्माण करना है
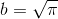 , जो आमतौर पर Q [x] में किसी बहुपद की जड़ नहीं है और Q के ऊपर कोई डिग्री नहीं है।
, जो आमतौर पर Q [x] में किसी बहुपद की जड़ नहीं है और Q के ऊपर कोई डिग्री नहीं है।
- एक नियमित हेप्टागन का निर्माण असंभव है। यह क्षेत्र से संख्या cos (2𝜋 / 7) और \ या sin (2 7/7) का निर्माण करने के लिए कम कर देता है। एकता z = e 2 sevent / 7 के सातवें अंश की जड़ x 7 -1 = (x-1) (x 6 ) है + x 5 + ... + 1) और Q के ऊपर डिग्री 6 है, क्योंकि दूसरा कारक इरेड्यूसिबल है। दूसरी ओर, z के पास L = Q (cos (2 7/7), sin (2𝜋 / 7), z = cos (2𝜋 / 7) + i sin (2𝜋 / 7) (L (i) के बाद से 2 डिग्री है। [L (i): L] = 2 इसलिए, L के पास Q पर 6/2 = 3 over 2 n की डिग्री है और यह उपलब्ध नहीं है।
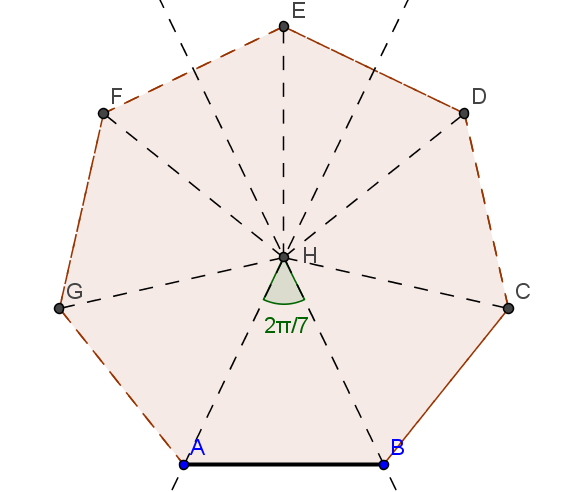
- एक नियमित 17-गॉन का निर्माण, इसके विपरीत, संभव है क्योंकि z = e 2 a / 17 रूट x 17 -1 = (x-1) (x 16 + x 15 + ... + 1) है और इसकी डिग्री 16 = 2 4 है over Q. सामान्य तौर पर, यह किसी भी p-gon के लिए काम करता है, जहाँ p एक प्रधान है जैसे कि p-1 = 2 n । इस तरह की संख्याओं को फर्मेट प्रिम्स कहा जाता है। पियरे फर्मेट ने स्वयं दावा किया कि फॉर्म 2 2 ^ एन +1 के सभी नंबर सरल, उनकी आदत के लिए सही, अप्रमाणित हैं। हालांकि, जल्द ही इसका खंडन कर दिया गया। नियमित 65537-गॉन, फ़र्मेट की अधिकतम ज्ञात अभाज्य संख्या के अनुरूप, 1894 में साधारण कम्पास और शासकों का उपयोग करते हुए, उत्कृष्ट धैर्य के व्यक्ति जोहान हर्म्स द्वारा बनाया गया था।
मुझे आशा है कि मैं प्रिय पाठकों को गणनाओं की एक बहुतायत के साथ बहुत ज्यादा नहीं थकता और मैं इस तरह के एक सरल उदाहरण का उपयोग करके सौंदर्य और गणित के विभिन्न वर्गों के करीब परस्पर संबंध का प्रदर्शन करने में सक्षम था। टिप्पणियों और टिप्पणियों को देखकर मुझे खुशी होगी।