इस पोस्ट में, हम भू-स्थानिक अनुक्रमण के बारे में बात करेंगे, जैसे कि R * -tree के रूप में एक डेटा संरचना और मैंने अपना पहला प्रोजेक्ट कैसे लागू किया।
तो चलिए शुरू करते हैं। स्नातक होने के तुरंत बाद, मुझे शिक्षकों के कार्यालय से एक प्रस्ताव मिला, जो कारों के लिए जीपीएस-निगरानी सेवाएं प्रदान करता है, जिसे मैंने स्वीकार किया। यहाँ यह है! अंत में, असली दिलचस्प परियोजनाएं! मेरा आनंद और उत्साह कोई सीमा नहीं जानता था। पहला काम जो मुझे दिया गया था, उसमें निम्नलिखित शब्द थे:
एक डेस्कटॉप एप्लिकेशन है, जिसमें माइलेज पर किसी भी रिपोर्ट, कारों के खर्च किए गए ईंधन इत्यादि के अलावा, वेक्टर नक्शे प्रदर्शित किए जाते हैं, जो वास्तविक समय में इन कारों की स्थिति के साथ, कार आंदोलनों के इतिहास और अन्य प्रकार के अन्य सामानों को ट्रैक करते हैं। अब यह सब गलत और अक्षम रूप से काम कर रहा है। कोई नहीं जानता कि इसे सही तरीके से कैसे लागू किया जाए। फिर से लिखने की जरूरत है...
मेरे हाथ में 160,000 लाइनों के लिए आवेदन का स्रोत कोड दिया गया था और वह यह है। कोई दस्तावेज नहीं, कुछ भी नहीं। जानकारी का एकमात्र स्रोत ये बहुत ही शिक्षक और योजना के स्रोत कोड में दुर्लभ टिप्पणियां "मैंने वास के अनुरोध पर n * x हटा दिया"। यह परियोजना 10 साल से अधिक पुरानी है, कार्यालय ग्राहकों के अनुरोधों को जल्द से जल्द पूरा करने के लिए बहुत ही वफादार और लचीला है। सभी तरह की इच्छाएं और सीटी लगभग अपने घुटनों पर पूरी कर ली हैं जो कि दस्तावेज नहीं थे। राक्षसी लापरवाही! लेकिन ऐसी परियोजनाएं किसी और के कोड को पार्स करने में कौशल को पंप करने में मदद करती हैं।
खैर, कार्य निर्धारित किया गया था, काम के लिए सामग्री थी। कोड के माध्यम से अफवाह फैलाना, सवाल पूछना, मैंने उस समय अपने आप को मामलों की वर्तमान स्थिति के लिए थोड़ा स्पष्ट किया:
- मानचित्र इन बिंदुओं के लिंक के साथ बिंदुओं और वस्तुओं की एक सरणी हैं
- स्क्रीन क्षेत्र को हिट करने वाली वस्तुओं को संपूर्ण खोज द्वारा निर्धारित किया जाता है।
- स्क्रीन पर ऑब्जेक्ट के आकार की गणना करके "मक्खी पर" ऑब्जेक्ट निर्धारित किया गया था या नहीं (यह 1-पिक्सेल घर प्रदर्शित करने पर सिस्टम संसाधनों को खर्च करने का कोई मतलब नहीं है)
छोटे आकार के नक्शे (शहर, जिला) का चित्रण सहनीय था। जब लोड हो रहा हो, तो क्षेत्र के देश के नक्शे को लोड करना, जिसमें सैकड़ों वेक्टर वस्तुएं हों, जिसमें कुल लाखों बिंदु हों, आप कल्पना कर सकते हैं। Googling और विषय पर बहुत सारी सामग्री पढ़ना, मैंने अपने आप के लिए 2 विकल्पों की पहचान की कि कैसे "इसे सही करें" सब कुछ:
- मानचित्र के पूरे क्षेत्र को एक निश्चित आकार के वर्गों में तोड़ें, जोड़ों पर गिरने वाली वस्तुओं को विभाजित करें, प्रत्येक ऑब्जेक्ट को एक वर्ग सूचकांक असाइन करें, डेटा को सॉर्ट करें और चलते-फिरते आवश्यक वस्तुओं की गणना करें;
- आर-ट्री का उपयोग करें।
थोड़ा सोचने के बाद, मैंने पहला विकल्प वापस फेंक दिया क्योंकि स्केल के स्तरों की एक निश्चित संख्या में संलग्न होना और प्रत्येक के लिए एक ग्रिड का निर्माण करना आवश्यक होगा। दूसरे विकल्प ने असीमित स्केलिंग का लाभ दिया, और सामान्य रूप से अधिक सार्वभौमिक लग रहा था। पहिया को सुदृढ़ नहीं करने के लिए, मैंने डेल्फी के तहत मौजूदा पुस्तकालयों की खोज करने का फैसला किया, क्योंकि इस पर प्रोजेक्ट लिखा गया था। पुस्तकालयों को कभी नहीं मिला और मैंने खुद को अनुक्रमित करने का निर्णय लिया।
आर-ट्री क्या है? इस संरचना को स्थानिक डेटा अनुक्रमण के लिए एंटोनिन गुटमैन द्वारा प्रस्तावित किया गया था, यह एक संतुलित पेड़ है और अनुभवजन्य टिप्पणियों के आधार पर विकसित किया गया था। एक पेड़ कई नेस्टेड आयतों में जगह तोड़ देता है। प्रत्येक ट्री नोड में न्यूनतम (न्यूनतम) और अधिकतम (अधिकतम) ऑब्जेक्ट्स की संख्या होती है। ट्री बिल्डिंग एल्गोरिदम के सही संचालन के लिए, यह आवश्यक है कि 2 <= minCount <= maxCount / 2 । प्रत्येक ऑब्जेक्ट की अपनी बाउंडिंग आयत है - MBR (न्यूनतम बाउंडिंग आयत)। एक एमबीआर नोड एक आयत है जो बच्चे के नोड्स के ऑब्जेक्ट के आयतों का वर्णन करता है।
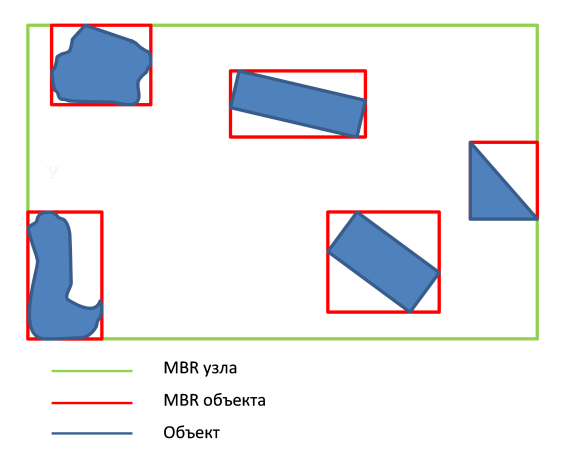
एक पेड़ वैकल्पिक रूप से वस्तुओं को सम्मिलित करके बनाया गया है। जब नोड ओवरफ्लो होता है, तो इसे विभाजित किया जाता है, यदि आवश्यक हो, तो सभी मूल नोड्स के विभाजन के बाद। किसी दिए गए डेटा संरचना के लिए खोज प्रश्नों की प्रभावशीलता कई मानदंडों पर निर्भर करती है:
- एमबीआर नोड्स के क्षेत्र को कम करना (वस्तुओं के बीच रिक्त स्थान को कम करना);
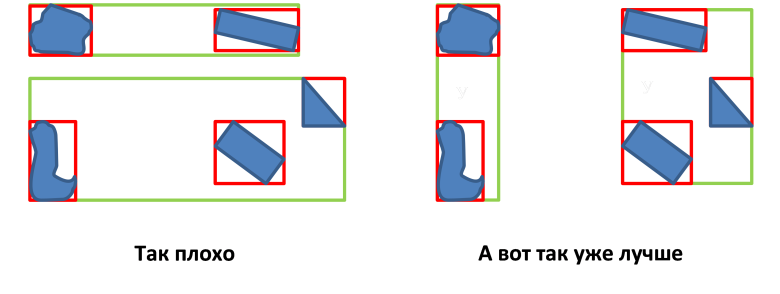
- एमबीआर नोड्स के अतिव्यापी क्षेत्रों के क्षेत्र का न्यूनतमकरण;
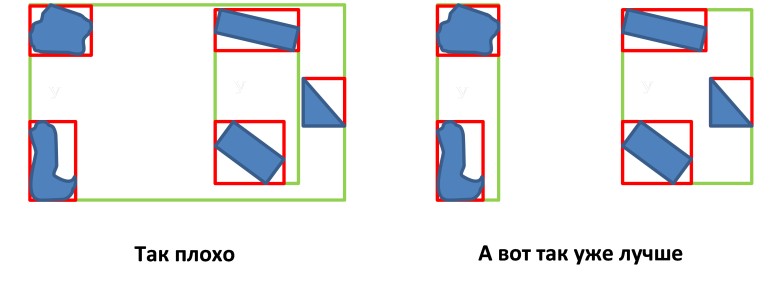
- एमबीआर नोड की परिधि को न्यूनतम करना;
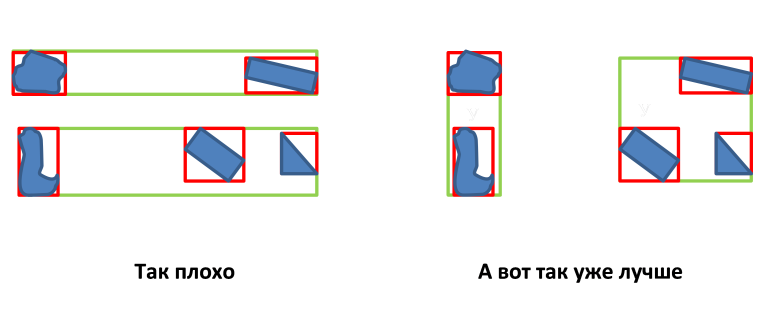
विभिन्न प्रकार के आर-पेड़ हैं, केवल भीड़ नोड के अंतिम और विभाजन की पसंद में भिन्नता है।
मैंने R * -tree क्यों चुना? मेरे व्यक्तिपरक मूल्यांकन में एंटोनिन गुटमैन (आर-ट्रीज़) द्वारा प्रस्तावित शास्त्रीय दृष्टिकोण, वास्तविक परियोजनाओं में उपयोग के लिए पूरी तरह से अनुपयुक्त है। एक उदाहरण के रूप में, मैं विकिपीडिया , अर्थात् आर-ट्री, जर्मन डाकघरों के लिए निर्मित सामग्री का हवाला दूंगा:
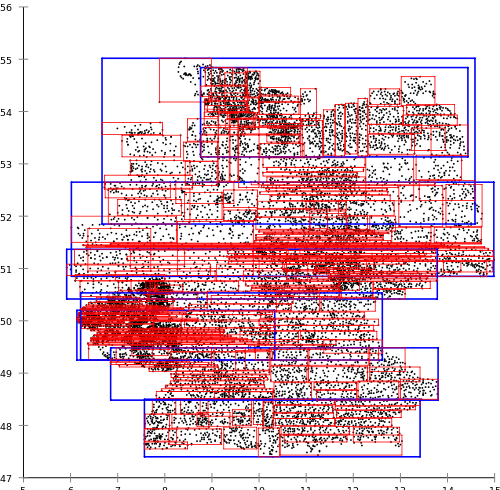
जब एक ही समय में, नोरबर्ट बेकमैन, हंस-पीटर क्रिगेल, राल्फ श्नाइडर और बर्नहार्ड सीजर द्वारा प्रस्तावित आर * ट्री एल्गोरिदम निम्नलिखित परिणाम देते हैं:
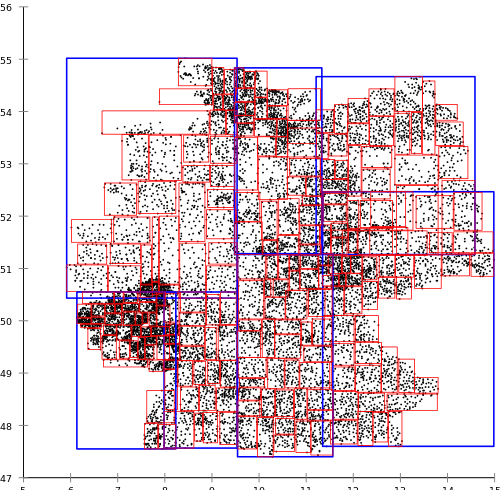
आर * -ट्री बनाने के लिए अधिक संसाधन-गहन है, लेकिन सामान्य आर-ट्री की तुलना में खोज प्रश्नों के लिए बेहतर परिणाम देता है।
इस बात पर विचार करें कि सम्मिलन कैसे होता है: इसमें एक शाखा (सबट्री) / नोड का चयन करने के लिए एल्गोरिदम और एक नोड को पूरा करने के लिए एक एल्गोरिथ्म शामिल है, जब यह भरा हुआ है।
सबट्री चयन एल्गोरिथम (चयन करें)
1. N को रूट नोड के रूप में सेट करें 2. यदि एन एंड नोड है, तो एन वापस करें 3.Inache 4. यदि N का बच्चा नोड्स अंतिम नोड्स (पत्तियां) हैं, 5. एक बच्चे के नोड एन का चयन करें जिसके एमबीआर को सम्मिलन पर ओवरलैप में सबसे छोटी वृद्धि की आवश्यकता होती है नोड के लिए वस्तु 6. यदि ओवरलैप में सबसे छोटी वृद्धि के साथ कई नोड हैं, तो उनमें से एक का चयन करें जिसे क्षेत्र में सबसे छोटी वृद्धि की आवश्यकता होती है 7. यदि क्षेत्र में सबसे छोटी वृद्धि के साथ कई नोड हैं, तो उनमें से एक नोड का चयन करें सबसे छोटे क्षेत्र के साथ 8. नहीं तो 9. एक बच्चे के नोड एन का चयन करें जिसके एमबीआर को क्षेत्र में सबसे छोटी वृद्धि की आवश्यकता होती है 10. यदि क्षेत्र में सबसे छोटी वृद्धि के साथ कई नोड हैं, तो सबसे छोटे क्षेत्र के साथ नोड का चयन करें 11. चयनित नोड पर एन सेट करें। 12. चरण 2 से पीछे हटें।
नोड विभाजन एल्गोरिथ्म (स्प्लिटनोड)
विभाजन विकल्प खोजने के लिए, आर * - ट्री निम्नलिखित विधि का उपयोग करता है: नोड्स को बाईं और दाईं सीमाओं के साथ प्रत्येक समन्वय अक्षों के साथ क्रमबद्ध किया जाता है। प्रत्येक सॉर्ट किए गए संस्करण के लिए, नोड्स को 2 समूहों में विभाजित किया जाता है ताकि k = [1 ... (maxCount - 2 * minCount + 2)] , पहले समूह में शामिल हैं (minCount - 1) + k नोड्स दूसरे में शेष हैं। इस तरह के प्रत्येक वितरण के लिए, निम्नलिखित संकेतकों की गणना की जाती है:
- क्षेत्र: क्षेत्र = क्षेत्र (पहले समूह का एमबीआर) + क्षेत्र (दूसरे समूह का एमबीआर)
- परिधि: मार्जिन = मार्जिन (पहले समूह का एमबीआर) + मार्जिन (दूसरे समूह का एमबीआर)
- ओवरलैप: ओवरलैप = क्षेत्र (पहले समूह का एमबीआर (दूसरे समूह का एमबीआर))
सबसे अच्छा वितरण निम्नलिखित एल्गोरिदम द्वारा निर्धारित किया जाता है:
1. कॉल का चयन करेंSSSSititx अक्ष का निर्धारण करने के लिए जिसके साथ वितरण होगा। 2. चयनित अक्ष पर सर्वोत्तम वितरण निर्धारित करने के लिए selectSplitIndex पर कॉल करें 3. वस्तुओं को 2 नोड्स पर असाइन करें
chooseSplitAxis
1. प्रत्येक अक्ष के लिए 2. बाईं ओर नोड्स को क्रमबद्ध करें, और फिर उनके एमबीआर की दाईं सीमाओं द्वारा। उपरोक्त वर्णित नोड्स को वितरित करें, एस की गणना करें - प्रत्येक वितरण के सभी परिधि का योग। 3. न्यूनतम एस के साथ एक अक्ष चुनें।
chooseSplitIndex
1. चयनित अक्ष के साथ, न्यूनतम ओवरलैप पैरामीटर के साथ एक वितरण का चयन करें 2. यदि न्यूनतम ओवरलैप पैरामीटर के साथ कई वितरण हैं, तो वितरण का चयन करें सबसे छोटे क्षेत्र के साथ।
वास्तव में खुद सम्मिलित करें (सम्मिलित करें)
1. कॉल selectSubStree, एन नोड निर्धारित करने के लिए एक तर्क के रूप में रूट नोड से गुजर रहा है, जिसमें वस्तु E का सम्मिलन होगा 2. यदि N में वस्तुओं की संख्या अधिकतम से कम है, 3. E को N में डालें 4. N और उसके सभी मूल नोड्स के लिए MBR अपडेट करें 5. अन्यथा, एन और ई के लिए स्प्लिटनोड को कॉल करें।
अपने लेख में R * ट्री के लेखकों का तर्क है कि इस संरचना का सबसे अच्छा प्रदर्शन minCount = maxCount * 40% के साथ हासिल किया गया है।
वह सब है। हमारा पेड़ बनाया गया है, और अब किसी दिए गए क्षेत्र में सही वस्तुओं को ढूंढना मुश्किल नहीं है:
किसी दिए गए क्षेत्र में वस्तुओं को खोजने के लिए एल्गोरिदम (FindObjectsInArea)
1. यदि वर्तमान नोड N परिमित है, 2. नोड एन में प्रत्येक बच्चे ऑब्जेक्ट ई के लिए, निर्धारित करें 3. यदि E खोज क्षेत्र को काटता है, तो E को खोज परिणाम R में जोड़ें। 4. नहीं तो 5. नोड एन में प्रत्येक बच्चे के नोड एन के लिए, निर्धारित करें 6. यदि n खोज क्षेत्र को काटता है, तो n के लिए findObjectsInArea पर कॉल करें
इसके बाद, हम बस
findObjectsInArea
कॉल
findObjectsInArea
, इसे रूट नोड और खोज क्षेत्र पास करते हैं।
बुनियादी एल्गोरिदम के संचालन को अधिक स्पष्ट रूप से प्रदर्शित करने के लिए, आइए कोड को देखें:
sortsy
// R*-tree unit RStar_tree; interface uses Windows, SysUtils, Math; const MAX_M = 16; // MIN_M = Round(MAX_M * 0.4); // type TObjArr = array of Integer; // TAxis = (X, Y); // chooseSplitAxis - TBound = (Left, Right); // (\) TGpsPoint = record // GPS (X = lon\Y = lat) X, Y: Double; end; TMBR = record // \\ MBR = Minimum Bounding Rectangle Left, Right: TGpsPoint; // left - right - end; TRObject = record // R-. mbr: TMBR; // idx: Integer; // , end; TRNode = class // private fmbr: TMBR; // FParent: Integer; // , - FChildren: array of Integer; // FObjects: array of TRObject; // . ( () (, , ) FisLeaf: Boolean; // () FLevel: Integer; // (0=) protected function getIsLeaf: Boolean; // FisLeaf function getChild(Index: Integer): Integer; // function getObject(Index: Integer): TRObject; // procedure setChild(Index: Integer; node_id: Integer); // procedure setObject(Index: Integer; obj: TRObject); // procedure setParent(parent_id: Integer); // - Procedure copy(node: TRNode); // Procedure clearObjects(); // Procedure clearChildren(); // public constructor Create; overload; constructor Create(node: TRNode); overload; destructor Destroy; override; property mbr: TMBR read fmbr write fmbr; // property isLeaf: Boolean read FisLeaf; // property Children[Index: Integer]: Integer read getChild write setChild; // property Objects[Index: Integer]: TRObject read getObject write setObject; // property Parent: Integer read FParent write setParent; // property Level: Integer read FLevel write FLevel; // function isIntersected(mbr1, mbr2: TMBR): Boolean; overload; // mbr1, mbr2 function isIntersected(mbr: TMBR): Boolean; overload; // MBR mbr function Overlap(mbr_ovrl: TMBR): Double; // MBR function Area: Double; overload; // MBR function Area(mbr: TMBR): Double; overload; // MBR function margin: Double; // MBR end; TRtree = class // private FNodeArr: array of TRNode; // FRoot: Integer; // FHeight: Integer; // Procedure QuickSort(var List: array of TRObject; iLo, iHi: Integer; axe: TAxis; bound: TBound); overload; // MBR. axe - , bound - (/) procedure QuickSort(var List: array of Integer; iLo, iHi: Integer; axe: TAxis; bound: TBound); overload; // MBR. axe - , bound - (/) Procedure splitNodeRStar(node_id: Integer; obj: TRObject); overload; // 2 R*-tree (page 325:: The R*-tree: An Efficient and Robust Access Method for Points and Rectangles+) node_id = obj = Procedure splitNodeRStar(splited_Node_Id, inserted_Node_Id: Integer); overload; // 2 R*-tree (page 325:: The R*-tree: An Efficient and Robust Access Method for Points and Rectangles+) splited_Node_Id = , inserted_Node_Id = Procedure updateMBR(node_id: Integer); overload; // MBR Procedure updateMBR(node: TRNode); overload; // MBR Procedure chooseSubtree(obj: TRObject; var node_id: Integer); // node_id obj. function chooseSplitAxis(obj: TRObject; node_id: Integer): TAxis; overload; // ( R*-tree) function chooseSplitAxis(nodeFather, nodeChild: Integer): TAxis; overload; // ( R*-tree) Procedure findObjectsInArea(mbr: TMBR; node_id: Integer; var obj: TObjArr); overload; // mbr function isRoot(node_id: Integer): Boolean; // node_id function newNode(): Integer; // . protected public constructor Create; destructor Destroy; override; Procedure insertObject(obj: TRObject); // Procedure findObjectsInArea(mbr: TMBR; var obj: TObjArr); overload; // mbr. (. .. , ) property Height: Integer read FHeight; // end; function toRObject(lx, ly, rx, ry: Double; idx: Integer): TRObject; overload; function toRObject(mbr: TMBR; idx: Integer): TRObject; overload; implementation function toRObject(lx, ly, rx, ry: Double; idx: Integer): TRObject; begin Result.mbr.Left.X := Min(lx, rx); Result.mbr.Left.Y := Min(ly, ry); Result.mbr.Right.X := Max(lx, rx); Result.mbr.Right.Y := Max(ly, ry); Result.idx := idx; end; function toRObject(mbr: TMBR; idx: Integer): TRObject; begin Result.mbr := mbr; Result.idx := idx; end; { TRNode } function TRNode.Area: Double; begin Result := (fmbr.Right.X - fmbr.Left.X) * (fmbr.Right.Y - fmbr.Left.Y); end; function TRNode.Area(mbr: TMBR): Double; begin Result := (mbr.Right.X - mbr.Left.X) * (mbr.Right.Y - mbr.Left.Y); end; procedure TRNode.clearChildren; begin SetLength(FChildren, 0); end; procedure TRNode.clearObjects; begin FisLeaf := False; SetLength(FObjects, 0); end; procedure TRNode.copy(node: TRNode); var i: Integer; begin SetLength(FObjects, Length(node.FObjects)); SetLength(FChildren, Length(node.FChildren)); if Length(FObjects) > 0 then begin for i := 0 to High(node.FObjects) do begin FObjects[i].idx := node.FObjects[i].idx; FObjects[i].mbr.Left.X := node.FObjects[i].mbr.Left.X; FObjects[i].mbr.Left.Y := node.FObjects[i].mbr.Left.Y; FObjects[i].mbr.Right.X := node.FObjects[i].mbr.Right.X; FObjects[i].mbr.Right.Y := node.FObjects[i].mbr.Right.Y; end; FisLeaf := True; end else begin for i := 0 to High(node.FChildren) do begin Children[i] := node.Children[i]; end; FisLeaf := False; end; fmbr.Left.X := node.fmbr.Left.X; fmbr.Left.Y := node.fmbr.Left.Y; fmbr.Right.X := node.fmbr.Right.X; fmbr.Right.Y := node.fmbr.Right.Y; FParent := node.Parent; FLevel := node.Level; end; constructor TRNode.Create(node: TRNode); begin Create; FParent := -10; copy(node); end; constructor TRNode.Create; begin inherited; FParent := -10; end; destructor TRNode.Destroy; begin SetLength(FObjects, 0); SetLength(FChildren, 0); inherited; end; function TRNode.getChild(Index: Integer): Integer; begin if High(FChildren) >= Index then begin Result := FChildren[Index]; end; end; function TRNode.getIsLeaf: Boolean; begin if Length(FObjects) > 0 then Result := True else Result := False; end; function TRNode.getObject(Index: Integer): TRObject; begin if High(FObjects) >= Index then begin Result := FObjects[Index]; end; end; function TRNode.isIntersected(mbr: TMBR): Boolean; begin Result := False; if (fmbr.Left.X <= mbr.Right.X) and (fmbr.Left.Y <= mbr.Right.Y) then begin if (fmbr.Right.X >= mbr.Left.X) and (fmbr.Right.Y >= mbr.Left.Y) then begin Result := True; end; end; end; function TRNode.margin: Double; begin Result := ((fmbr.Right.X - fmbr.Left.X) + (fmbr.Right.Y - fmbr.Left.Y)) * 2; end; function TRNode.Overlap(mbr_ovrl: TMBR): Double; var X, Y: Double; begin X := Min(mbr_ovrl.Right.X, fmbr.Right.X) - Max(mbr_ovrl.Left.X, fmbr.Left.X); if X <= 0 then begin Result := 0; Exit; end; Y := Min(mbr_ovrl.Right.Y, fmbr.Right.Y) - Max(mbr_ovrl.Left.Y, fmbr.Left.Y); if Y <= 0 then begin Result := 0; Exit; end; Result := X * Y; end; function TRNode.isIntersected(mbr1, mbr2: TMBR): Boolean; begin Result := False; if (mbr1.Left.X <= mbr2.Right.X) and (mbr1.Left.Y <= mbr2.Right.Y) then begin if (mbr1.Right.X >= mbr2.Left.X) and (mbr1.Right.Y >= mbr2.Left.Y) then begin Result := True; end; end; end; procedure TRNode.setChild(Index, node_id: Integer); begin if High(FChildren) >= Index then begin FChildren[Index] := node_id; FisLeaf := False; end else begin if ((Index) <= (MAX_M - 1)) and (Index >= 0) then begin SetLength(FChildren, Index + 1); FChildren[Index] := node_id; FisLeaf := False; end; end; end; procedure TRNode.setObject(Index: Integer; obj: TRObject); begin if High(FObjects) >= Index then begin FObjects[Index] := obj; FisLeaf := True; end else begin if ((Index) <= (MAX_M - 1)) and (Index >= 0) then begin SetLength(FObjects, Index + 1); FObjects[Index] := obj; FisLeaf := True; end; end; end; procedure TRNode.setParent(parent_id: Integer); begin if parent_id >= 0 then FParent := parent_id; end; { TRtree } function TRtree.chooseSplitAxis(obj: TRObject; node_id: Integer): TAxis; var arr_obj: array of TRObject; i, j, k, idx: Integer; node_1, node_2: TRNode; perimeter_min, perimeter: Double; begin SetLength(arr_obj, MAX_M + 1); if not FNodeArr[node_id].isLeaf then Exit; for i := 0 to High(FNodeArr[node_id].FObjects) do begin arr_obj[i] := FNodeArr[node_id].FObjects[i]; end; arr_obj[ High(arr_obj)] := obj; node_1 := TRNode.Create; node_2 := TRNode.Create; perimeter_min := 999999; for i := 0 to 1 do // begin perimeter := 0; for j := 0 to 1 do // () begin node_1.clearObjects; node_2.clearObjects; QuickSort(arr_obj, 0, High(arr_obj), TAxis(i), TBound(j)); for k := 1 to MAX_M - MIN_M * 2 + 2 do // begin idx := 0; while idx < ((MIN_M - 1) + k) do // (MIN_M - 1) + k begin node_1.Objects[idx] := arr_obj[idx]; idx := idx + 1; end; for idx := idx to High(arr_obj) do // begin node_2.Objects[idx - ((MIN_M - 1) + k)] := arr_obj[idx]; end; updateMBR(node_1); updateMBR(node_2); perimeter := perimeter + ((node_1.mbr.Right.X - node_1.mbr.Left.X) * 2 + (node_2.mbr.Right.Y - node_2.mbr.Left.Y) * 2); end; end; if perimeter <= perimeter_min then begin Result := TAxis(i); perimeter_min := perimeter; end; perimeter := 0; end; SetLength(arr_obj, 0); FreeAndNil(node_1); FreeAndNil(node_2); end; function TRtree.chooseSplitAxis(nodeFather, nodeChild: Integer): TAxis; var arr_node: array of Integer; i, j, k, idx: Integer; node_1, node_2: TRNode; perimeter_min, perimeter: Double; begin SetLength(arr_node, MAX_M + 1); for i := 0 to High(FNodeArr[nodeFather].FChildren) do begin arr_node[i] := FNodeArr[nodeFather].FChildren[i]; end; arr_node[ High(arr_node)] := nodeChild; perimeter_min := 999999; node_1 := TRNode.Create; node_2 := TRNode.Create; for i := 0 to 1 do // begin perimeter := 0; for j := 0 to 1 do // () begin node_1.clearChildren; node_2.clearChildren; QuickSort(arr_node, 0, High(arr_node), TAxis(i), TBound(j)); for k := 1 to MAX_M - MIN_M * 2 + 2 do // begin idx := 0; while idx < ((MIN_M - 1) + k) do // (MIN_M - 1) + k begin node_1.Children[idx] := arr_node[idx]; idx := idx + 1; end; for idx := idx to High(arr_node) do // begin node_2.Children[idx - ((MIN_M - 1) + k)] := arr_node[idx]; end; updateMBR(node_1); updateMBR(node_2); perimeter := perimeter + node_1.margin + node_2.margin; end; end; if perimeter <= perimeter_min then begin Result := TAxis(i); perimeter_min := perimeter; end; perimeter := 0; end; FreeAndNil(node_1); FreeAndNil(node_2); SetLength(arr_node, 0); end; procedure TRtree.chooseSubtree(obj: TRObject; var node_id: Integer); var i, id_child: Integer; min_overlap_enlargement: Double; // Overlap_enlargement: Double; area_enlargement: Double; idChild_overlap: array of Integer; { . , , MBR } idChild_area: array of Integer; { . , MBR , MBR } id_zero: Integer; { MBR ( MBR) } enlargement_mbr: TMBR; // MBR dx, dy, dspace: Double; // MBR x, y has_no_enlargement: Boolean; // begin if FNodeArr[node_id].isLeaf then // , begin Exit; end; SetLength(idChild_overlap, 1); SetLength(idChild_area, 1); dx := 0; dy := 0; dspace := 9999999; id_zero := 0; has_no_enlargement := False; min_overlap_enlargement := 999999; if FNodeArr[FNodeArr[node_id].Children[0]].isLeaf then // () begin { } for i := 0 to High(FNodeArr[node_id].FChildren) do begin id_child := FNodeArr[node_id].FChildren[i]; Overlap_enlargement := FNodeArr[id_child].Area(obj.mbr) - FNodeArr[id_child].Overlap(obj.mbr); if Overlap_enlargement <= min_overlap_enlargement then begin if Overlap_enlargement = min_overlap_enlargement then // begin SetLength(idChild_overlap, Length(idChild_overlap) + 1); idChild_overlap[ High(idChild_overlap)] := i; end else // begin min_overlap_enlargement := Overlap_enlargement; if Length(idChild_overlap) = 1 then // idChild_overlap[0] := i else begin SetLength(idChild_overlap, 1); // , 1 idChild_overlap[0] := i end; end; end; end; if Length(idChild_overlap) = 1 then // 1 begin node_id := FNodeArr[node_id].Children[idChild_overlap[0]]; chooseSubtree(obj, node_id); // Exit; end; end else // begin SetLength(idChild_overlap, Length(FNodeArr[node_id].FChildren)); for i := 0 to High(FNodeArr[node_id].FChildren) do // idChild_overlap, ( , idChild_overlap ) idChild_overlap[i] := i; end; { } for i := 0 to High(idChild_overlap) do begin id_child := FNodeArr[node_id].FChildren[idChild_overlap[i]]; enlargement_mbr.Left.X := Min(obj.mbr.Left.X, FNodeArr[id_child].mbr.Left.X); enlargement_mbr.Left.Y := Min(obj.mbr.Left.Y, FNodeArr[id_child].mbr.Left.Y); enlargement_mbr.Right.X := Max(obj.mbr.Right.X, FNodeArr[id_child].mbr.Right.X); enlargement_mbr.Right.Y := Max(obj.mbr.Right.Y, FNodeArr[id_child].mbr.Right.Y); area_enlargement := FNodeArr[id_child].Area(enlargement_mbr) - FNodeArr[id_child].Area; if area_enlargement <= dspace then begin if area_enlargement = dspace then // begin SetLength(idChild_area, Length(idChild_area) + 1); idChild_area[ High(idChild_area)] := i; end else // begin dspace := area_enlargement; if Length(idChild_area) = 1 then // idChild_area[0] := i else begin SetLength(idChild_area, 1); // , 1 idChild_area[0] := i end; end; end; end; if Length(idChild_area) = 1 then // , MBR begin node_id := FNodeArr[node_id].Children[idChild_area[0]]; chooseSubtree(obj, node_id); // end else // ( MBR ) MBR begin dspace := 999999; for i := 0 to High(idChild_area) do begin id_child := FNodeArr[node_id].Children[idChild_area[i]]; if FNodeArr[id_child].Area < dspace then begin id_zero := idChild_area[i]; dspace := FNodeArr[id_child].Area; end; end; node_id := FNodeArr[node_id].Children[id_zero]; chooseSubtree(obj, node_id); end; end; constructor TRtree.Create; begin inherited; SetLength(FNodeArr, 1); FNodeArr[0] := TRNode.Create; FRoot := 0; FNodeArr[FRoot].FisLeaf := True; end; destructor TRtree.Destroy; var i: Integer; begin for i := 0 to High(FNodeArr) do FreeAndNil(FNodeArr[i]); SetLength(FNodeArr, 0); inherited; end; procedure TRtree.findObjectsInArea(mbr: TMBR; node_id: Integer; var obj: TObjArr); var i: Integer; begin if isRoot(node_id) then SetLength(obj, 0); if not FNodeArr[node_id].isLeaf then begin for i := 0 to High(FNodeArr[node_id].FChildren) do begin if FNodeArr[FNodeArr[node_id].Children[i]].isIntersected(mbr) then findObjectsInArea(mbr, FNodeArr[node_id].Children[i], obj); end; end else begin for i := 0 to High(FNodeArr[node_id].FObjects) do begin if FNodeArr[node_id].isIntersected(mbr, FNodeArr[node_id].Objects[i].mbr) then begin SetLength(obj, Length(obj) + 1); obj[ High(obj)] := FNodeArr[node_id].Objects[i].idx; end; end; end; end; procedure TRtree.findObjectsInArea(mbr: TMBR; var obj: TObjArr); begin findObjectsInArea(mbr, FRoot, obj); end; procedure TRtree.insertObject(obj: TRObject); var node_id: Integer; begin node_id := FRoot; chooseSubtree(obj, node_id); if Length(FNodeArr[node_id].FObjects) < MAX_M then // begin FNodeArr[node_id].Objects[ High(FNodeArr[node_id].FObjects) + 1] := obj; updateMBR(node_id); end else // begin splitNodeRStar(node_id, obj); // end; end; function TRtree.isRoot(node_id: Integer): Boolean; begin if node_id = FRoot then Result := True else Result := False; end; function TRtree.newNode: Integer; begin SetLength(FNodeArr, Length(FNodeArr) + 1); FNodeArr[ High(FNodeArr)] := TRNode.Create; Result := High(FNodeArr); end; procedure TRtree.QuickSort(var List: array of TRObject; iLo, iHi: Integer; axe: TAxis; bound: TBound); var Lo: Integer; Hi: Integer; T: TRObject; Mid: Double; begin Lo := iLo; Hi := iHi; case bound of Left: case axe of X: Mid := List[(Lo + Hi) div 2].mbr.Left.X; Y: Mid := List[(Lo + Hi) div 2].mbr.Left.Y; end; Right: case axe of X: Mid := List[(Lo + Hi) div 2].mbr.Right.X; Y: Mid := List[(Lo + Hi) div 2].mbr.Right.Y; end; end; repeat case bound of Left: case axe of X: begin while List[Lo].mbr.Left.X < Mid do Inc(Lo); while List[Hi].mbr.Left.X > Mid do Dec(Hi); end; Y: begin while List[Lo].mbr.Left.Y < Mid do Inc(Lo); while List[Hi].mbr.Left.Y > Mid do Dec(Hi); end; end; Right: case axe of X: begin while List[Lo].mbr.Right.X < Mid do Inc(Lo); while List[Hi].mbr.Right.X > Mid do Dec(Hi); end; Y: begin while List[Lo].mbr.Right.Y < Mid do Inc(Lo); while List[Hi].mbr.Right.Y > Mid do Dec(Hi); end; end; end; if Lo <= Hi then begin T := List[Lo]; List[Lo] := List[Hi]; List[Hi] := T; Inc(Lo); Dec(Hi); end; until Lo > Hi; if Hi > iLo then QuickSort(List, iLo, Hi, axe, bound); if Lo < iHi then QuickSort(List, Lo, iHi, axe, bound); end; procedure TRtree.QuickSort(var List: array of Integer; iLo, iHi: Integer; axe: TAxis; bound: TBound); var Lo: Integer; Hi: Integer; T: Integer; Mid: Double; begin Lo := iLo; Hi := iHi; case bound of Left: case axe of X: Mid := FNodeArr[List[(Lo + Hi) div 2]].mbr.Left.X; Y: Mid := FNodeArr[List[(Lo + Hi) div 2]].mbr.Left.Y; end; Right: case axe of X: Mid := FNodeArr[List[(Lo + Hi) div 2]].mbr.Right.X; Y: Mid := FNodeArr[List[(Lo + Hi) div 2]].mbr.Right.Y; end; end; repeat case bound of Left: case axe of X: begin while FNodeArr[List[Lo]].mbr.Left.X < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Left.X > Mid do Dec(Hi); end; Y: begin while FNodeArr[List[Lo]].mbr.Left.Y < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Left.Y > Mid do Dec(Hi); end; end; Right: case axe of X: begin while FNodeArr[List[Lo]].mbr.Right.X < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Right.X > Mid do Dec(Hi); end; Y: begin while FNodeArr[List[Lo]].mbr.Right.Y < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Right.Y > Mid do Dec(Hi); end; end; end; if Lo <= Hi then begin T := List[Lo]; List[Lo] := List[Hi]; List[Hi] := T; Inc(Lo); Dec(Hi); end; until Lo > Hi; if Hi > iLo then QuickSort(List, iLo, Hi, axe, bound); if Lo < iHi then QuickSort(List, Lo, iHi, axe, bound); end; procedure TRtree.splitNodeRStar(splited_Node_Id, inserted_Node_Id: Integer); var axe: TAxis; parent_id, new_child_id: Integer; node_1, node_2, node_1_min, node_2_min: TRNode; i, j, k: Integer; arr_node: array of Integer; area_overlap_min, area_overlap, // area_min, Area: Double; // begin if FNodeArr[splited_Node_Id].isLeaf then Exit; if isRoot(splited_Node_Id) then begin parent_id := newNode; // id FNodeArr[FRoot].Parent := parent_id; // id , FNodeArr[parent_id].Children[0] := FRoot; // id FNodeArr[parent_id].Level := FNodeArr[FNodeArr[parent_id].Children[0]].Level + 1; // 1 FRoot := parent_id; // id id FHeight := FHeight + 1; // end else begin parent_id := FNodeArr[splited_Node_Id].Parent; end; SetLength(arr_node, MAX_M + 1); for i := 0 to High(arr_node) - 1 do arr_node[i] := FNodeArr[splited_Node_Id].Children[i]; arr_node[ High(arr_node)] := inserted_Node_Id; node_1_min := TRNode.Create; node_2_min := TRNode.Create; node_1 := TRNode.Create; node_2 := TRNode.Create; axe := chooseSplitAxis(splited_Node_Id, inserted_Node_Id); area_overlap_min := 9999999; area_min := 9999999; for i := 0 to 1 do begin QuickSort(arr_node, 0, High(arr_node), axe, TBound(i)); for k := MIN_M - 1 to MAX_M - MIN_M do begin node_1.clearChildren; node_2.clearChildren; j := 0; while j <= k do begin node_1.Children[j] := arr_node[j]; j := j + 1; end; for j := k to High(arr_node) - 1 do begin node_2.Children[j - k] := arr_node[j + 1]; end; updateMBR(node_1); updateMBR(node_2); area_overlap := node_1.Overlap(node_2.mbr); if area_overlap < area_overlap_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_overlap_min := area_overlap; end else begin if area_overlap = area_overlap_min then // begin Area := node_1.Area + node_2.Area; // if Area < area_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_min := Area; end; end; end; end; end; node_1_min.Level := FNodeArr[splited_Node_Id].Level; node_2_min.Level := FNodeArr[splited_Node_Id].Level; FNodeArr[splited_Node_Id].copy(node_1_min); // () FNodeArr[splited_Node_Id].Parent := parent_id; new_child_id := newNode; // FNodeArr[new_child_id].copy(node_2_min); // FNodeArr[new_child_id].Parent := parent_id; // id parent FreeAndNil(node_1); FreeAndNil(node_2); FreeAndNil(node_1_min); FreeAndNil(node_2_min); for i := 0 to High(FNodeArr[new_child_id].FChildren) do // Parent id begin FNodeArr[FNodeArr[new_child_id].Children[i]].Parent := new_child_id end; if Length(FNodeArr[parent_id].FChildren) < MAX_M then // begin FNodeArr[parent_id].Children[ High(FNodeArr[parent_id].FChildren) + 1] := new_child_id; // id updateMBR(parent_id); end else // begin splitNodeRStar(parent_id, new_child_id); // end; end; procedure TRtree.splitNodeRStar(node_id: Integer; obj: TRObject); var axe: TAxis; parent_id, new_child_id: Integer; node_1, node_2, node_1_min, node_2_min: TRNode; i, j, k: Integer; arr_obj: array of TRObject; area_overlap_min, area_overlap, // area_min, Area: Double; // begin if not FNodeArr[node_id].isLeaf then Exit; if isRoot(node_id) then begin parent_id := newNode; // id FNodeArr[FRoot].Parent := parent_id; // id , FNodeArr[parent_id].Children[0] := FRoot; // id FNodeArr[parent_id].Level := FNodeArr[FNodeArr[parent_id].Children[0]].Level + 1; // 1 FRoot := parent_id; // id id FHeight := FHeight + 1; // end else begin parent_id := FNodeArr[node_id].Parent; end; SetLength(arr_obj, MAX_M + 1); for i := 0 to High(arr_obj) - 1 do arr_obj[i] := FNodeArr[node_id].Objects[i]; arr_obj[ High(arr_obj)] := obj; node_1_min := TRNode.Create; node_2_min := TRNode.Create; node_1 := TRNode.Create; node_2 := TRNode.Create; axe := chooseSplitAxis(obj, node_id); area_overlap_min := 9999999; area_min := 9999999; for i := 0 to 1 do begin QuickSort(arr_obj, 0, High(arr_obj), axe, TBound(i)); for k := MIN_M - 1 to MAX_M - MIN_M do begin node_1.clearObjects; node_2.clearObjects; j := 0; while j <= k do begin node_1.Objects[j] := arr_obj[j]; j := j + 1; end; for j := k to High(arr_obj) - 1 do begin node_2.Objects[j - k] := arr_obj[j + 1]; end; updateMBR(node_1); updateMBR(node_2); area_overlap := node_1.Overlap(node_2.mbr); if area_overlap < area_overlap_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_overlap_min := area_overlap; end else begin if area_overlap = area_overlap_min then // begin Area := node_1.Area + node_2.Area; // if Area < area_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_min := Area; end; end; end; end; end; node_1_min.Level := 0; node_2_min.Level := 0; FNodeArr[node_id].copy(node_1_min); // () FNodeArr[node_id].Parent := parent_id; updateMBR(node_id); new_child_id := newNode; // FNodeArr[new_child_id].copy(node_2_min); // FNodeArr[new_child_id].Parent := parent_id; // id parent updateMBR(new_child_id); FreeAndNil(node_1); FreeAndNil(node_2); FreeAndNil(node_1_min); FreeAndNil(node_2_min); if Length(FNodeArr[parent_id].FChildren) < MAX_M then // begin FNodeArr[parent_id].Children[ High(FNodeArr[parent_id].FChildren) + 1] := new_child_id; // id updateMBR(parent_id); end else // begin splitNodeRStar(parent_id, new_child_id); // end; end; procedure TRtree.updateMBR(node: TRNode); var i, idx: Integer; changed: Boolean; begin changed := False; node.fmbr.Left.X := 9999; node.fmbr.Left.Y := 9999; node.fmbr.Right.X := 0; node.fmbr.Right.Y := 0; if node.isLeaf then begin for i := 0 to High(node.FObjects) do begin if node.FObjects[i].mbr.Left.X < node.mbr.Left.X then begin node.fmbr.Left.X := node.FObjects[i].mbr.Left.X; changed := True; end; if node.FObjects[i].mbr.Left.Y < node.mbr.Left.Y then begin node.fmbr.Left.Y := node.FObjects[i].mbr.Left.Y; changed := True; end; if node.FObjects[i].mbr.Right.X > node.mbr.Right.X then begin node.fmbr.Right.X := node.FObjects[i].mbr.Right.X; changed := True; end; if node.FObjects[i].mbr.Right.Y > node.mbr.Right.Y then begin node.fmbr.Right.Y := node.FObjects[i].mbr.Right.Y; changed := True; end; end; end else begin for i := 0 to High(node.FChildren) do begin idx := node.FChildren[i]; if FNodeArr[idx].mbr.Left.X < node.mbr.Left.X then begin node.fmbr.Left.X := FNodeArr[idx].mbr.Left.X; changed := True; end; if FNodeArr[idx].mbr.Left.Y < node.mbr.Left.Y then begin node.fmbr.Left.Y := FNodeArr[idx].mbr.Left.Y; changed := True; end; if FNodeArr[idx].mbr.Right.X > node.mbr.Right.X then begin node.fmbr.Right.X := FNodeArr[idx].mbr.Right.X; changed := True; end; if FNodeArr[idx].mbr.Right.Y > node.mbr.Right.Y then begin node.fmbr.Right.Y := FNodeArr[idx].mbr.Right.Y; changed := True; end; end; end; if changed then begin if node.Parent >= 0 then updateMBR(node.Parent); end; end; procedure TRtree.updateMBR(node_id: Integer); var i, idx: Integer; changed: Boolean; begin changed := False; FNodeArr[node_id].fmbr.Left.X := 9999; FNodeArr[node_id].fmbr.Left.Y := 9999; FNodeArr[node_id].fmbr.Right.X := 0; FNodeArr[node_id].fmbr.Right.Y := 0; if FNodeArr[node_id].isLeaf then begin for i := 0 to High(FNodeArr[node_id].FObjects) do begin if FNodeArr[node_id].FObjects[i].mbr.Left.X < FNodeArr[node_id].mbr.Left.X then begin FNodeArr[node_id].fmbr.Left.X := FNodeArr[node_id].FObjects[i].mbr.Left.X; changed := True; end; if FNodeArr[node_id].FObjects[i].mbr.Left.Y < FNodeArr[node_id].mbr.Left.Y then begin FNodeArr[node_id].fmbr.Left.Y := FNodeArr[node_id].FObjects[i].mbr.Left.Y; changed := True; end; if FNodeArr[node_id].FObjects[i].mbr.Right.X > FNodeArr[node_id].mbr.Right.X then begin FNodeArr[node_id].fmbr.Right.X := FNodeArr[node_id].FObjects[i].mbr.Right.X; changed := True; end; if FNodeArr[node_id].FObjects[i].mbr.Right.Y > FNodeArr[node_id].mbr.Right.Y then begin FNodeArr[node_id].fmbr.Right.Y := FNodeArr[node_id].FObjects[i].mbr.Right.Y; changed := True; end; end; end else begin for i := 0 to High(FNodeArr[node_id].FChildren) do begin idx := FNodeArr[node_id].FChildren[i]; if FNodeArr[idx].mbr.Left.X < FNodeArr[node_id].mbr.Left.X then begin FNodeArr[node_id].fmbr.Left.X := FNodeArr[idx].mbr.Left.X; changed := True; end; if FNodeArr[idx].mbr.Left.Y < FNodeArr[node_id].mbr.Left.Y then begin FNodeArr[node_id].fmbr.Left.Y := FNodeArr[idx].mbr.Left.Y; changed := True; end; if FNodeArr[idx].mbr.Right.X > FNodeArr[node_id].mbr.Right.X then begin FNodeArr[node_id].fmbr.Right.X := FNodeArr[idx].mbr.Right.X; changed := True; end; if FNodeArr[idx].mbr.Right.Y > FNodeArr[node_id].mbr.Right.Y then begin FNodeArr[node_id].fmbr.Right.Y := FNodeArr[idx].mbr.Right.Y; changed := True; end; end; end; if changed then begin if FNodeArr[node_id].Parent >= 0 then updateMBR(FNodeArr[node_id].Parent); end; end; end.
कार्यान्वयन के बाद, जो कुछ करना बाकी था, वह वेक्टर मैप ऑब्जेक्ट्स को परतों में विभाजित करना था, इन परतों को अधिकतम पैमाने पर सेट करें जिस पर वे प्रदर्शित होंगे और प्रत्येक परत के लिए R * -tree का निर्माण करेंगे।
परिणाम वीडियो पर देखे जा सकते हैं: