👰🏾 👨‍👦‍👦 ▶️ एक तंत्रिका नेटवर्क के दिमाग में क्या होता है और उनकी मदद कैसे की जाती है 👬 😴 🤙🏽

हाल ही में, न्यूरल नेटवर्क के बारे में कई लेख हैबे पर दिखाई दिए हैं। इनमें से, रोसेनब्लैट पर्सेप्ट्रॉन के बारे में लेख बहुत दिलचस्प लग रहा था: रोसेनब्लट पर्सेप्ट्रॉन - इतिहास द्वारा भूल और आविष्कार क्या है? और रोसेनब्लट पर्सेप्ट्रॉन में पहली "यादृच्छिक" परत की भूमिका क्या है । उनमें, कई अन्य लोगों की तरह, इस तथ्य के बारे में बहुत कुछ लिखा गया है कि नेटवर्क समस्याओं को हल करने के साथ सामना करते हैं, और कुछ हद तक अपने ज्ञान को सामान्य करते हैं। लेकिन मैं किसी भी तरह इन सामान्यीकरण और निर्णय प्रक्रिया की कल्पना करना चाहूंगा। व्यवहार में यह देखने के लिए कि वहाँ पर अवधारणात्मक ने क्या सीखा, और यह महसूस करने के लिए कि वह कितनी सफलतापूर्वक सफल हुई। शायद एआई के क्षेत्र में मानवता की उपलब्धि के बारे में एक कड़वी विडंबना का सामना करना पड़ रहा है।

हमारे पास भाषा के रूप में C # होगा, सिर्फ इसलिए कि मैंने हाल ही में इसे सीखने का फैसला किया है। मैंने सबसे सरल उदाहरणों में से दो को देखा: एक एकल-परत रोसेनब्लाट पर्सेप्ट्रॉन, जो त्रुटि सुधार द्वारा सिखाया गया था, और एक बहु-परत रूमेलहार्ट परसेप्ट्रॉन, जो पीछे प्रसार विधि द्वारा सिखाया गया था। उन लोगों के लिए, जो मेरे जैसे हैं, वे वास्तव में वहां जो कुछ सीखते हैं, उसमें दिलचस्पी हो गई और वे वास्तव में कितना सामान्य रूप से सक्षम हैं, बिल्ली का स्वागत करते हैं।

चेतावनी! बहुत सारी तस्वीरें। कोड के टुकड़े।

सबसे पहले, मैं आपको एक तंत्रिका नेटवर्क सीखने की प्रक्रिया की प्रशंसा करना चाहता हूं। 1000 प्रशिक्षण बिंदुओं के बाद प्रत्येक फ्रेम। प्रशिक्षण की गति और इस हजार चक्रों के लिए मानक त्रुटि का संकेत दिया जाता है।

कोड से, मैं केवल वही दिखाऊंगा जो दूसरों के लिए उपयोगी हो सकता है जो अपने हाथों से सब कुछ करना चाहते हैं या मेरे निष्कर्ष की शुद्धता को सत्यापित करना चाहते हैं। महत्वपूर्ण तत्वों का कोड परीक्षण परियोजना की जड़ से फाड़ा गया है जिसमें इसे लॉन्च किया गया था, इसलिए कहीं न कहीं उन तत्वों के लिंक हो सकते हैं जो मैं प्रदान नहीं करता हूं। लेकिन कोड काम कर रहा है, सभी चित्र मेरे प्रशिक्षण परियोजना के स्क्रीनशॉट हैं।

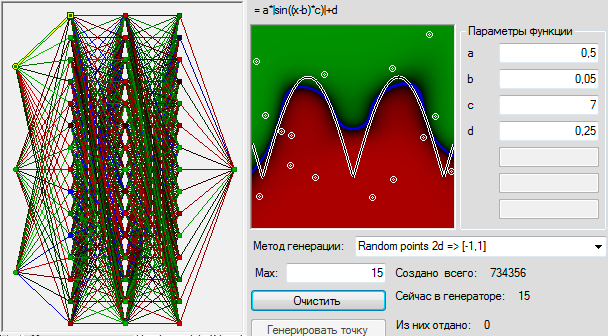
पहले आपको एक कार्य चुनने की आवश्यकता है ताकि आप इसे देखें, और यह तुरंत स्पष्ट हो जाता है कि क्या अवधारणात्मक ने कुछ भी सीखा है और क्या। दो निर्देशांक (एक्स और वाई) लें, और उनमें बहुत सारे यादृच्छिक बिंदुओं को फेंक दें। यह इनपुट होगा। चलो कुछ ग्राफ खींचते हैं और यह निर्धारित करने के लिए कि क्या इस ग्राफ के ऊपर या नीचे एक बिंदु है, अवधारणकर्ता से पूछें। दूसरी ओर, रोसेनब्लैट परसेप्ट्रान, पूरी संख्या में काम करता है, और वास्तव में यह कार्य बहुत सरल है। फिर आइए प्रत्येक निर्देशांक को पूर्णांक में गोल करें और बाइनरी फॉर्म में प्रतिनिधित्व करें: एक अंक, एक इनपुट। एकरूपता के लिए, समन्वित श्रेणी (0.1) को सभी उदाहरणों में माना जाता है, इसलिए राउंड करने से पहले इसे अधिकतम पूर्णांक मान से गुणा किया जाना चाहिए।

उदाहरण के लिए, प्रत्येक समन्वय को दो-बिट संख्या के रूप में कल्पना करें। यादृच्छिक संख्याओं की एक जोड़ी (0.2, 0.7) ग्राफ के ऊपर एक बिंदु की ओर इशारा करती है, फिर चक्कर लगाने के बाद यह (1,3) जाएगा और हमें निम्नलिखित प्रशिक्षण उदाहरण देगा:

new double[]{0.2, 0.7} => new NeuralTask { Preview = new double[]{0.25, 0,75, 1}, Input=new double[] {0,1,1,1}, Output=new double[]{1}}

एक फ़ंक्शन जो यादृच्छिक संख्या को केस स्टडी में परिवर्तित करता है, वह कुछ इस तरह दिखता है:

रूपांतरण समारोह

  var Convertion = (double[] random, double value) => { var input = new double[]{Math.Floor(random [0]*0x4)/0x4, Math.Floor(random [1]*0x4)/0x4}, byte x = (byte)(input[0] * 4); byte y = (byte)(input[1] * 4); int res = (y > value * 4 ? 1 : 0); return new NeuralTask() { input = new double[4]{ (x&2)>>1, x&1, (y&2)>>1, y&1}, output = new double[1] { res }, preview = new double[3] { input[0], input[1], res } }; };

यहाँ यह स्पष्ट किया जाना चाहिए कि यह सब शैक्षिक और अनुसंधान उद्देश्यों के लिए किया गया था, इसलिए इसे गति और अस्पष्ट सौंदर्य के लिए अनुकूलित नहीं किया गया था, लेकिन इसे कहीं लिखा गया था ताकि किसी भी बोधगम्य अवधारणात्मक कार्यक्रम के लिए सुविधाजनक हो। इसलिए, विशेष रूप से, इनपुट और आउटपुट डेटा डबल में हैं। यह इस तरह की एक साधारण तस्वीर है। यदि प्रत्येक अक्ष 256 खंडों में कटा हुआ है, और फ़ंक्शन को लेना अधिक कठिन है, तो ठीक है, या थोड़ा अधिक जटिल है:

इसके बाद, हरा रंग - शून्य से अधिक मूल्य, अधिक संतृप्त, अधिक से अधिक संख्या, लाल - शून्य से कम मूल्य, नीला - 0 के बराबर मान और उनकी तत्काल आसपास के क्षेत्र।

स्रोत कोड

परसेप्ट्रोन में ही एक सिनाप्स होता है:

वर्ग सिंक

  public class Synaps { private double weight; /// <summary>   </summary> virtual public double Weight { get { return weight; } set { if (weight != value) { weight = value; if (axon != null) ChangeActionPotentialHandler(axon.ActionPotential); } } } /// <summary>    . ,  ,   ,     ,      .</summary> private IAxon axon; //   ,    . public IAxon Axon { get { return axon; } set { //    ,       . if (axon != null) axon.RemoveChangeActionPotentialHandler(ChangeActionPotentialHandler); axon = value; if (axon != null) { axon.AddChangeActionPotentialHandler(ChangeActionPotentialHandler); ChangeActionPotentialHandler(axon.ActionPotential); } } } public double ActionPotential; /// <summary>  ,     .</summary> protected Action WhenActionPotentialhanged; public void AddActionPotentialChangeHandler(Action handler) { WhenActionPotentialhanged += handler; } public void RemoveActionPotentialChangeHandler(Action handler) { WhenActionPotentialhanged -= handler; } virtual protected void ChangeActionPotentialHandler(double axonActionPotential) { ActionPotential = axonActionPotential * weight; //      ,       . if (WhenActionPotentialhanged != null) WhenActionPotentialhanged); //          } }

कुछ भी अप्रत्याशित नहीं है, सिवाय इसके कि संख्या डबल में संग्रहीत की जाती है और मानक घटना के बजाय, एक कस्टम का उपयोग किया जाता है। अब एक न्यूरॉन। IAxon इंटरफ़ेस के सभी सामान्य न्यूरॉन्स हमारे पास हैं:

इंटरफ़ेस IAxon

  public interface IAxon { /// <summary>  .</summary> double ActionPotential { get; } /// <summary>    .</summary> void AddChangeActionPotentialHandler(Action<double> handler); void RemoveChangeActionPotentialHandler(Action<double> handler); /// <summary>,        .</summary> PointF Position { get; set; } /// <summary>      .</summary> string Name { get; set; } }

यह भी अप्रत्याशित नहीं है, सिवाय स्थिति के, जहां न्यूरॉन आकर्षित करना है।

एक इनपुट के रूप में, संवेदी न्यूरॉन्स का उपयोग किया जाता है, जिसे सीधे सेट किया जा सकता है:

वर्ग SensoryNeuron

  public class SensoryNeuron : IAxon { protected double actionPotential; public double ActionPotential { get { return actionPotential; } set { if (actionPotential != value) { actionPotential = value; if (WhenChangeActionPotential != null) WhenChangeActionPotential(actionPotential); } } } }

अंत में, काफी सामान्यीकृत रूप में ही न्यूरॉन:

कक्षा न्यूरॉन

  /// <summary> .     </summary> public class Neuron : IAxon { /// <summary>  ,      .    ,     ,     .</summary> public Synaps[] Synapses = new Synaps[0]; /// <summary>  , ,            .</summary> protected bool synapsPotentialChanged = false; /// <summary>      .  ,  ,   . </summary> public void AppendSinaps(Synaps target) { //     .  , , ,      ,     . Synapses = Synapses.Concat(new Synaps[1] { target }).ToArray(); target.AddActionPotentialChangeHandler(ChangeSynapsPotentialHandler); //   . synapsPotentialChanged = true; } virtual protected void ChangeSynapsPotentialHandler() { synapsPotentialChanged = true; } /// <summary>   .     ,    .</summary> protected DTransferFunction transferFunctionDelegate; public virtual DTransferFunction TransferFunction { get { return transferFunctionDelegate; } set { transferFunctionDelegate = value; } } /// <summary>             . </summary> public virtual void Excitation() { if (!synapsPotentialChanged) return; //        synapsPotentialChanged = false; synapsPotentials = 0; for (int i = 0; i < Synapses.Length; i++) synapsPotentials += Synapses[i].ActionPotential; double newValue = transferFunctionDelegate(synapsPotentials); if (actionPotential != newValue) { //        . ,   . actionPotential = newValue; if (WhenChangeActionPotential != null) WhenChangeActionPotential(actionPotential); } } }

यहां:

सक्रियण समारोह

  /// <summary>        . </summary> /// <param name="argument">  </param> /// <returns>    </returns> public delegate double DTransferFunction(double argument); DTransferFunction BarrierTransferFunction = (double x) => x <= 0 ? 0 : 1;

अंत में, यह सब एक साथ हमें एक तंत्रिका नेटवर्क और इसके प्रशिक्षण के लिए एक एल्गोरिथ्म मिलता है:

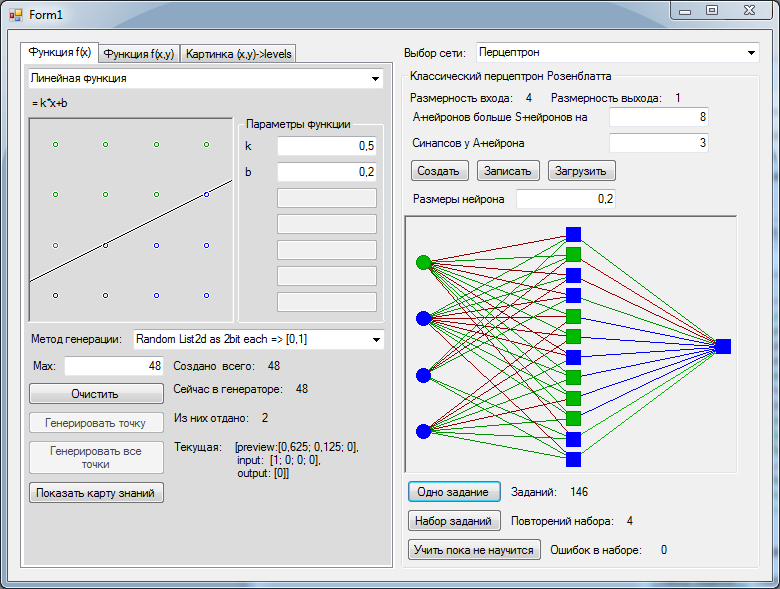
वर्ग NeuralNetwork, PerceptronClassic, ErrorCorrection

  abstract public class NeuralNetwork { /// <summary>  </summary> public SensoryNeuron[] Input = new SensoryNeuron[0]; /// <summary> ///            ,    .      . ///           ,          . /// </summary> public Neuron[] ExcitationOrder = new Neuron[0]; /// <summary>  </summary> public Neuron[] Output = new Neuron[0]; /// <summary> ,       </summary> /// <param name="input">   - </param> /// <param name="output">   </param> abstract public void create(uint input, uint output); public void execute(double[] data) { //               for (int i = 0; i < Input.Length && i < data.Length; i++) { Input[i].ActionPotential = data[i]; } for (int i = 0; i < ExcitationOrder.Length; i++) ExcitationOrder[i].Excitation(); } public double[] Result() { // return output.Select(s => s.ActionPotential).ToArray(); //TODO     Linq  . double[] res = new double[Output.Length]; for (int i = 0; i < res.Length; i++) res[i] = Output[i].ActionPotential; return res; } } public class PerceptronClassic : NeuralNetwork { //     ,    public int neuronCountsOverSensoric = 15; //     public int ANeuronSynapsCount; //      public Neuron[] Layer; //        override public void create(uint inputCount, uint outputCount) { rnd = rndSeed >= 0 ? new Random(rndSeed) : new Random(); //   this.Input = new SensoryNeuron[inputCount]; for (int i = 0; i < inputCount; i++) Input[i] = new SensoryNeuron() {Name = "S" + i}; //    -  Layer = new Neuron[inputCount + neuronCountsOverSensoric]; for (int i = 0; i < Layer.Length; i++) { //    Layer[i] = new RosenblattNeuron(); //         SensoryNeuron[] sub = Input.OrderBy((cell) => rnd.NextDouble()).Take(ANeuronSynapsCount).ToArray(); //   ,    for (int j = 0; j < sub.Length; j++) { Synaps s = new Synaps(); s.Axon = sub[j]; s.Weight = rnd.Next(2) * 2 - 1; Layer[i].AppendSinaps(s); } } //     . for (int i = 0; i < Layer.Length; i++) Layer[i].Name = "A" + i; //   -   Output = new Neuron[outputCount]; for (int i = 0; i < Output.Length; i++) { Output[i] = new RosenblattNeuron(); Output[i].Name = "R" + i; //        for (int j = 0; j < Layer.Length; j++) { Synaps s = new Synaps(); s.Axon = Layer[j]; Output[i].AppendSinaps(s); //   0 } } //       int lastIndex = 0; ExcitationOrder = new Neuron[Layer.Length + Output.Length]; foreach (Neuron cell in Layer) ExcitationOrder[lastIndex++] = cell; foreach (Neuron cell in Output) ExcitationOrder[lastIndex++] = cell; } } /// <summary>   .</summary> public class ErrorCorrection : LearningAlgorythm { // ,        override protected double LearnNet(double[] required) { double error = 0; for (int i = 0; i < required.Length && i < net.Output.Length; i++) { if (required[i] != net.Output[i].ActionPotential) { error += 1; //     for (int j = 0; j < (net as PerceptronClassic).Layer.Length; j++) //    ,   if ((net as PerceptronClassic).Layer[j].ActionPotential > 0) //      foreach (RosenblattNeuron cell in net.Output) //    ,       //    – ,   ,   – .    . cell.Synapses[j].Weight += required[i] <= 0 ? -1 : 1; } } return error; } /// <summary>       </summary> public void LearnTasksSet() { if (data == null) { Console.WriteLine("  "); return; } data.Reset(); LearnedTaskSetsCount++; ErrorsInSet = LearnedTasksInSetCount = 0; int max = 1000; while (data.MoveNext() && --max >= 0) LearnCurrentTask(); //     ,    . } /// <summary>         .</summary> /// <param name="loops">    </param> public void LearnSetManyTimesUntilSuccess(int loops) { for (int i = 0; i < loops; i++) { LearnTasksSet(); if (ErrorsInSet == 0) { break; } } } }

डेटा स्रोत Enumerable<NeuralTask>

और प्रत्येक रीसेट पर, यह क्रम में बिंदुओं को यादृच्छिक क्रम में पुनर्व्यवस्थित करता है।

सब कुछ तैयार है, आप दौड़ सकते हैं।

धुरी प्रति दो बिट्स के सबसे सरल कार्य के लिए, इसलिए हम एक उपयुक्त वियोज्य अपघटन खोजने के लिए भाग्यशाली थे, हमें 12 से अधिक इनपुटों को परत करने के लिए 8 न्यूरॉन्स को जोड़ना था। तीसरे प्रयास में एक उपयुक्त अपघटन का पता चला था। परसेप्ट्रॉन ने सभी 16 संभावित मूल्यों को अचूक रूप से वर्गीकृत किया।

यहां आप देख सकते हैं कि केवल 16 संभावित मूल्य हैं, और मैंने अधिक उत्पन्न किया। ताकि सभी संभावित विकल्पों को कवर करने के लिए यादृच्छिक संख्या की गारंटी हो।

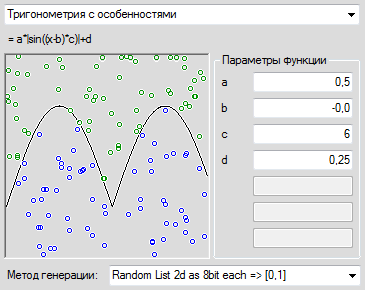
चूंकि सब कुछ इतना अद्भुत है, चलो थोड़ी अधिक जटिल समस्या पर चलते हैं, जहां प्रत्येक अक्ष के लिए हमारे पास मानों के 256 संस्करण हैं। हम सबसे सरल फ़ंक्शन पर विचार करते हैं। शुरुआत के लिए, हम 64 अंक उत्पन्न करते हैं। न्यूरॉन्स की परत में इनपुट की तुलना में केवल 20 अधिक हैं - 36 टुकड़े। और तुरंत सफलता।

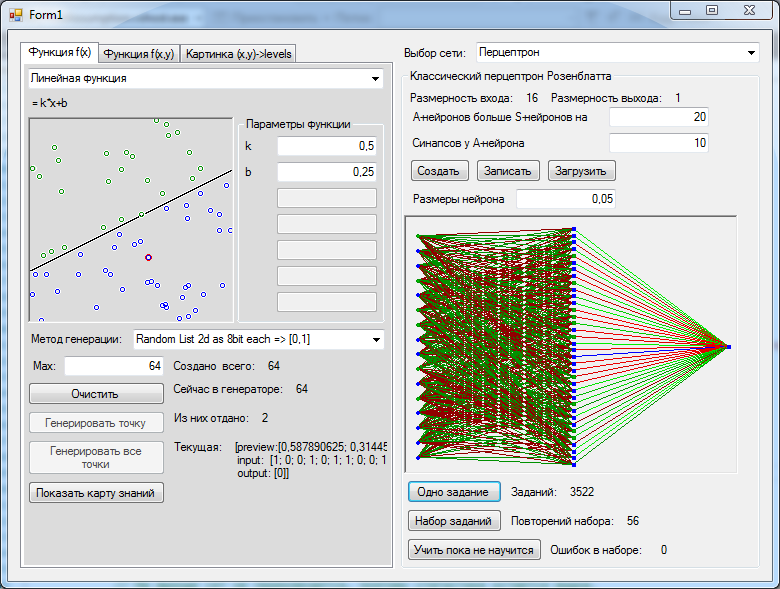
और अब हम सबसे दिलचस्प करेंगे। हम प्राप्त नेटवर्क को लेते हैं और चित्र में उन सभी संभावित मूल्यों को खींचते हैं जो नेटवर्क सभी बिंदुओं पर उत्पन्न करता है। और यहाँ सबसे दुखद बात निकलती है। नेटवर्क द्वारा प्राप्त सामान्यीकरण का स्तर बहुत प्रभावशाली नहीं है।

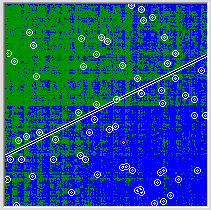
यह पता चला है कि बहुत व्यापक शब्दों में नेटवर्क यह दर्शाता है कि नियमितता उसे प्रदान किए गए बिंदुओं के पीछे छिपी हुई है। आइए अध्ययन किए जा रहे फ़ंक्शन पर अधिक संपूर्ण डेटा के साथ नेटवर्क प्रदान करने का प्रयास करें। हम 256 अंक उत्पन्न करते हैं। 36 न्यूरॉन्स, पिछली बार के रूप में, अब नेटवर्क के लिए एक उपयुक्त रैखिक रूप से वियोज्य अपघटन का सामना करने के लिए पर्याप्त नहीं है। अब हमें 70 सहयोगी न्यूरॉन्स बनाने की जरूरत है, कार्यों के प्रशिक्षण सेट को 615 बार चलाएं और कूलर को वैक्यूम करें ताकि प्रोसेसर सिर्फ एक सेकंड के प्रशिक्षण में खुशी के साथ गर्म न हो। नेटवर्क द्वारा हासिल किया गया सामान्यीकरण बेहतर हो गया है, लेकिन नग्न आंखों के साथ यह स्पष्ट है कि प्राप्त सुधार के प्रयासों के लिए अनुपातहीन है।

दिलों में, हम 2048 डॉट्स के एक स्थान को कवर करते हैं। हमें साहचर्य परत में 266 न्यूरॉन्स बनाने के लिए मजबूर किया जाता है, प्रति न्यूरॉन की इष्टतम संख्या का चयन करें (यह 8 निकलता है), एक सेट 411 बार सीखें (जब तक नेटवर्क गलतियां करना बंद नहीं करता है) और प्राप्त परिणाम को देखें।

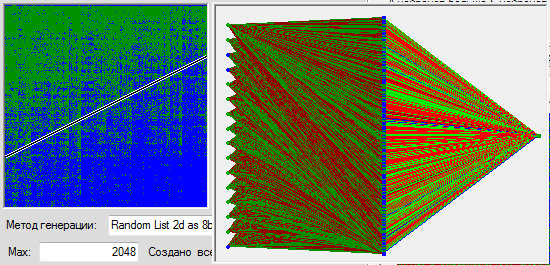
मुझे आपके बारे में पता नहीं है, लेकिन कुछ ऐसा है जो मैं गुणात्मक सुधार नहीं देखता हूं। नेटवर्क नियमित रूप से हृदय द्वारा सभी मूल्यों को याद करता है, न कि कुछ हद तक यह प्रस्तावित नियमितता के सामान्यीकरण के करीब। और सामान्य तौर पर यह स्पष्ट है कि नेटवर्क द्वारा किए गए विचारशील निष्कर्षों की प्रकृति इतनी अधिक नहीं है कि उसके द्वारा किए गए कार्य की प्रकृति पर निर्भर करती है।

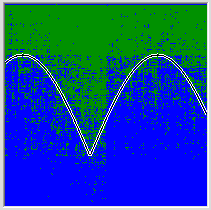
धन्यवाद, निश्चित रूप से, कम से कम यह जानने में सक्षम होने के लिए। ऐसा लगता है कि प्रमेय सही हैं, और यदि मेरे पास पर्याप्त न्यूरॉन्स हैं, तो मुझे इस कार्य के लिए कम से कम सभी 65536 संभावित विकल्पों को याद करने के लिए नेटवर्क मिल सकता है, लेकिन हमें लगभग 1500-2000 न्यूरॉन्स और पानी के ठंडा होने की आवश्यकता है। इस तरह के नेटवर्क में निहित सभी जानकारी को याद रखने के लिए, हमें प्रत्येक सिनैप्स के लिए 5 बिट्स (एक्सोन संख्या और वजन बिट के लिए 4 बिट्स) की आवश्यकता होती है, प्रत्येक न्यूरॉन 16 बिट्स के अक्षतंतु वजन मूल्य और सभी सिंकैप्स के लिए 40 बिट्स के लिए। और एक प्रशिक्षण उदाहरण का वजन 17 बिट है। 2048 अंकों के साथ हमारे उदाहरण में, यह पता चला है कि प्रशिक्षण की जानकारी केवल दो बार प्राप्त होती है, जितना कि प्राप्त नेटवर्क के बारे में जानकारी।

सुविधाजनक कार्य

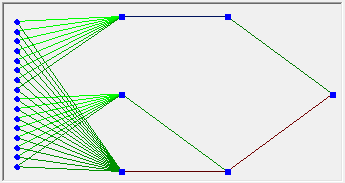तो समस्या क्या है? ऐसी धूमिल तस्वीर का कारण क्या है? आइए विश्लेषणात्मक रूप से समस्या को हल करने का प्रयास करें। माना कि हमारे पास एक परसेप्ट्रॉन है, लेकिन केवल पहली परत का वजन, साथ ही दूसरा, प्रशिक्षित किया जा सकता है। दूसरी परत में, हमारे पास केवल तीन न्यूरॉन्स हैं। पहला पहले 8 इनपुट से जुड़ा है और इसमें कोई बाधा नहीं है, लेकिन बस एक रैखिक सक्रियण फ़ंक्शन है। दूसरा न्यूरॉन समान है, लेकिन केवल दूसरे 8 बिट्स को सामान्य निर्देशांक में परिवर्तित करने के लिए जिम्मेदार है। तीसरा एक सभी के साथ जुड़ा हुआ है, एक बाधा फ़ंक्शन है और 1 देने के लिए डिज़ाइन किया गया है यदि कम से कम एक इनपुट में कम से कम कुछ है। अगली परत में, न्यूरॉन्स में से दो को फिर से अभिव्यक्त किया जाता है, फिर बिना किसी बाधा कार्य के, लेकिन फ़ंक्शन के मापदंडों को दर्शाते हुए बहुत महत्वपूर्ण भार के साथ। और अंत में, अंतिम न्यूरॉन दो इनपुट संकेतों की तुलना करेगा। सरल, तार्किक और थोड़ा दिलचस्प नहीं। हालांकि, यह इस कार्य के लिए शामिल न्यूरॉन्स और सिनेप्स की न्यूनतम संभव संख्या है। अब यह कल्पना करने की कोशिश करें कि आपको सिंगल-लेयर परसेप्ट्रॉन में इनमें से किसी भी ऑपरेशन को कितने न्यूरॉन्स को व्यक्त करने की आवश्यकता है, जिनकी पहली लेयर में सिनैप्स में केवल -1 और 1. हो सकते हैं, उदाहरण के लिए, 8 बिट्स को एक नंबर में परिवर्तित करना। मैं आपको बताता हूं - आपको लगभग 512 टुकड़े न्यूरॉन्स की आवश्यकता है, और हमने अभी तक इसकी तुलना करना शुरू नहीं किया है।

यही है, समस्या यह नहीं है कि रोसेनब्लट पर्सेप्ट्रॉन इस डेटासेट को नहीं सीख सकता है। समस्या यह है कि उसे करना बहुत असुविधाजनक है। जो लोग बड़ी संख्या के प्रमेय के साथ दोस्त हैं, वे यह पता लगाने की कोशिश कर सकते हैं कि इसके लिए उपयुक्त एक रैखिक रूप से अलग होने वाले अपघटन को खोजने की संभावना क्या है। रोसेनब्लाट परसेप्ट्रॉन उन समस्याओं को हल करने में सहज है जो अच्छी तरह से धब्बेदार नीले-हरे रंग की धुंधली ढाल के रूप में प्रस्तुत की जाती हैं, लेकिन जब ऐसा नहीं होता है तो सब कुछ दुखी हो जाता है।

और बहुपरत रूमेलहार्ट परसेप्ट्रॉन के बारे में क्या?

लेकिन क्या होगा यदि समस्याएं केवल सिंगल-लेयर रोसेनब्लैट पेसेप्ट्रॉन के लिए हैं, और पीछे प्रसार विधि द्वारा प्रशिक्षित मल्टीसेलेबिक पेसेप्ट्रॉन के लिए, सब कुछ बहुत अच्छा होगा, और यहां तक कि जादुई भी होगा? आइए कोशिश करते हैं।

स्रोत कोड

सबसे पहले, अब हम मौजूदा मूल्यों पर न्यूरॉन के सक्रियण समारोह के पहले व्युत्पन्न की गणना के कार्य को जोड़ देंगे। इस सबको बहुत आसानी से अनुकूलित किया जा सकता है और व्युत्पन्न की गणना को सीधे उस फार्मूले में सिंक्रनाइज़ किया जा सकता है जिसमें इसे लागू किया जाएगा, लेकिन हमारा काम सब कुछ गति देना नहीं है, बल्कि यह पता लगाना है कि यह कैसे काम करता है। इसलिए, एक अलग कार्य:

सक्रियण समारोह से व्युत्पन्न

  /// <summary>      . </summary> /// <param name="argument">  </param> /// <param name="funcResult">  ,    </param> /// <returns>       .</returns> public delegate double DTransferFunctionDerivative(double argument, double funcResult);

एक उदाहरण के रूप में, हम उपयोग करते हैं, उदाहरण के लिए, हाइपरटेन्जेंट:

 DTransferFunction Function = (x) => Math.Tanh(x), DTransferFunctionDerivative Derivative = (x, th) => (1 - th) * (1 + th)

अब तो न्यूरॉन ही। यह केवल उस में भिन्न होता है, मूल्य के प्रत्येक गणना पर, यह इनपुट संकेतों के योग द्वारा अपनी व्युत्पत्ति की गणना भी करता है, और एक चर की उपस्थिति से जिसमें त्रुटि के पीछे प्रसार के लिए उपयोग किए जाने वाले मूल्य को संग्रहीत किया जाएगा।

वर्ग NeuronWithDerivative

  public class NeuronWithDerivative : Neuron { /// <summary>    .           .</summary> protected DTransferFunctionDerivative transferFunctionDerivativeDelegate; /// <summary></summary> override public DTransferFunctionDerivative TransferFunction { get { return transferFunctionDerivativeDelegate; } set { transferFunctionDerivativeDelegate = value; } } /// <summary>        </summary> protected double actionPotentialDerivative = 0; /// <summary>        .</summary> public double ActionPotentialDerivative { get { return actionPotentialDerivative; } } /// <summary>     . ,    .   .</summary> public double BackProprigationParametr = 0; public override void Excitation() { base.Excitation(); actionPotentialDerivative = transferFunctionDerivativeDelegate(synapsPotentials, actionPotential); } }

हाल ही में, मैं LINQ का उपयोग करना पसंद करता हूं, क्योंकि प्रायोगिक कोड लिखना आसान और तेज़ है। इस मामले की सुविधा के लिए, मेरा छोटा सा घर समारोह, अपनी क्षमताओं का विस्तार। मैं इसे List.ForEach के बजाय उपयोग करता हूं ताकि कॉल सुंदर और एकल-पंक्ति हो।

स्थिर वर्ग उपकरण

  static class Tools { /// <summary>         .</summary> /// <param name="source">   .</param> /// <param name="func">,   .</param> public static void Each<SequenceType>(this IEnumerator<SequenceType> source, Action<SequenceType> func) { while (source.MoveNext()) func(source.Current); } /// <summary>             .</summary> /// <param name="source">   .</param> /// <param name="func">,   .     -   .      .   -  .</param> public static void Each<SequenceType>(this IEnumerator<SequenceType> source, Action<SequenceType, int> func) { for (int i = 0; source.MoveNext(); i++) func(source.Current, i); } /// <summary>         .</summary> /// <param name="source">   .</param> /// <param name="func">,   .</param> public static void Each<SequenceType>(this IEnumerable<SequenceType> source, Action<SequenceType> func) { source.GetEnumerator().Each(func); } /// <summary>             .</summary> /// <param name="source">   .</param> /// <param name="func">,   .     -   .      .   -  .</param> public static void Each<SequenceType>(this IEnumerable<SequenceType> source, Action<SequenceType, int> func) { source.GetEnumerator().Each(func); } }

class RumelhartPerceptron

  //          . public class RumelhartPerceptron : NeuralNetwork { /// <summary>   .  .</summary> DTransferFunctionDerivative TransferFunctionDerivative; /// <summary>    ,      </summary> public int[] NeuronsCount = new int[0]; override public void create(uint input, uint output) { //  . Input = (new SensoryNeuron[input]).Select((empty, index) => new SensoryNeuron(){Name = "S[" + index + "]"}).ToArray(); //     Func<string, NeuronWithDerivative> create = (name) => { NeuronWithDerivative neuron = new NeuronWithDerivative(); neuron.Name = name; neuron.TransferFunction = TransferFunction; neuron.TransferFunctionDerivative = TransferFunctionDerivative; return neuron; }; Func<IAxon, Synaps> createSynaps = (axon) => { Synaps s = new Synaps(); s.Axon = axon; return s; }; /// <summary>  </summary> //       NeuronWithDerivative[][] Layers = NeuronsCount.Select((count, layer) => Enumerable.Range(0, count).Select(index => create("A[" + layer + "][" + index + "]")).ToArray()).ToArray(); //      //   Output = Enumerable.Range(0, (int)output).Select(index => create("R[" + index + "]")).ToArray(); //         . Layers[0].Each(neuron => { Input.Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); }); //  ,    ,      . Layers.Skip(1).Each((layer, layerIndex) => { layer.Each(neuron => { Layers[layerIndex].Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); }); }); //        Output.Each(neuron => { Layers.Last().Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); }); //      ExcitationOrder = Layers.SelectMany(layer => layer).Concat(Output).ToArray(); //       -1  +1 Random rnd = new Random(); ExcitationOrder.Each(neuron => neuron.Synapses.Each(synaps => synaps.Weight = rnd.NextDouble() * 2 - 1)); } }

, , . LINQ , . , , .

class BackPropagationLearning

  public class BackPropagationLearning : LearningAlgorythm { // ,     public double LearningSpeed = 0.01; override protected double LearnNet(double[] required) { double[] errors = net.Output.Select((neuron, index) => neuron.ActionPotential - required[index]).ToArray(); //     .     ,                . net.ExcitationOrder.Cast<NeuronWithDerivative>().Each(neuron => { neuron.BackProprigationParametr = 0; }); //   BackProprigationParametr    dE/dS[i] = dE/dO[i] * F'[i](S[i]) //          . BP[i] = dE/dO[i] * F'[i] = 2*(O[i]-T[i])*F'[i]; net.Output.Cast<NeuronWithDerivative>().Each((neuron, index) => { neuron.BackProprigationParametr = 2 * errors[index] * neuron.ActionPotentialDerivative; }); //      ,       BP[j] = SUM( dE/dO[i] * F'[i] * W[j,i] ) * F'[j] = SUM ( BP[i] * W[j,i] * F'[j]) net.ExcitationOrder.Reverse().Cast<NeuronWithDerivative>().Each(neuron => { neuron.Synapses.SkipWhile(synaps => !(synaps.Axon is NeuronWithDerivative)).Each(synaps => { (synaps.Axon as NeuronWithDerivative).BackProprigationParametr += neuron.BackProprigationParametr * (synaps.Axon as NeuronWithDerivative).ActionPotentialDerivative * synaps.Weight; }); }); //     ,    delta W[i,j] = -speed * dE/dS[j] * X[i]; net.ExcitationOrder.Reverse().Cast<NeuronWithDerivative>().Each(neuron => { neuron.Synapses.Each(synaps => { synaps.Weight += -LearningSpeed * neuron.BackProprigationParametr * synaps.Axon.ActionPotential; }); }); //     . (        ,  ). return errors.Select(e => e * e).Average(); } public void LearnSomeTime(int sek) { DateTime begin = DateTime.Now; while (TimeSpan.FromTicks(DateTime.Now.Ticks - begin.Ticks).Seconds < sek) { LearnTasksSet(); } } }

यहाँ एक ऐसा कोड है। यह केवल विहित कार्यान्वयन से भिन्न होता है, जिसमें सीखने की गति को पीछे की ओर फैलाने वाली त्रुटि में नहीं डाला जाता है, बल्कि उपयोग से तुरंत पहले वजन में परिवर्तन से गुणा किया जाता है। हम चुकता त्रुटियों की राशि को कम करते हैं, जैसा कि विकिपीडिया हमें सिखाता है, जो इस भाग में हैबरोइट्स द्वारा भरा गया था।

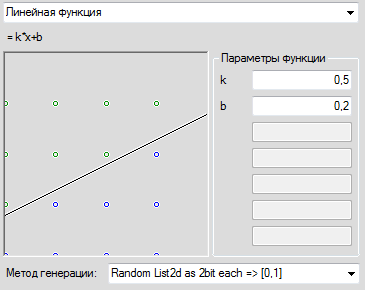
हम किस नेटवर्क को शुरू करने के लिए अपना नेटवर्क खिसकाते हैं? चलिए प्लॉट [0,1] से समान x और y लेते हैं। ऐसे बिंदु जो ग्राफ़ से अधिक हैं, हम +1 के नीचे दिए गए बिंदुओं पर नेटवर्क के आउटपुट पर +1 प्रदर्शित होने की उम्मीद करेंगे। इसके अलावा, हम केस स्टडी के एक से अधिक निश्चित अनुक्रम बनाएंगे, और हम हर बार नए केस स्टडी बनाएंगे, ताकि यह न कहा जा सके कि नेटवर्क को अंतरिक्ष के कुछ महत्वपूर्ण हिस्से के बारे में जानकारी नहीं थी। हम प्रति सेट 1000 टुकड़ों के चर के बने पैक देते हैं। पूर्वावलोकन एक बिंदु नहीं दिखाता है, लेकिन आखिरी कुछ सिर्फ सुंदरता के लिए बनाया गया है। यह किसी भी तरह निकलता है।

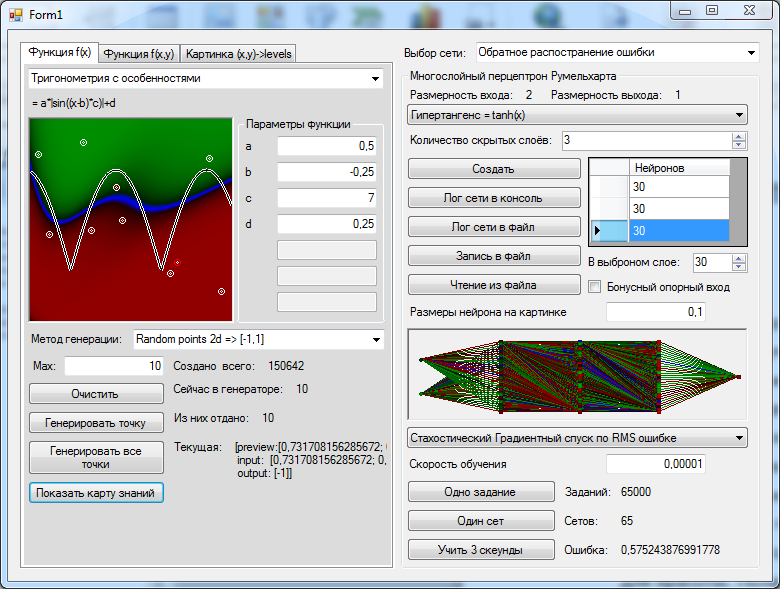
एक तंत्रिका नेटवर्क बनाएँ। विकिपीडिया हमें बताता है कि तीन परतें पर्याप्त होनी चाहिए। ताकि यह छोटा प्रतीत न हो, चलो प्रति परत में 30 न्यूरॉन्स जोड़ते हैं। आइए अनुवर्तन संयोजक एल्गोरिदम के कुछ सिमुलेशन सिखाने की कोशिश करें।, धीरे-धीरे मैन्युअल रूप से सीखने की गति को कम कर रहा है, क्योंकि पिछले 1000 प्रशिक्षण उदाहरणों के मानक त्रुटि में सुधार बंद हो जाता है। यह कार्यक्रम की घोषणा करने के लिए बहुत आलसी था, क्योंकि मेरा लेख उस बारे में नहीं है। हम ट्रेन करते हैं, हम ट्रेन करते हैं, और अंत में, जब नेटवर्क की गुणवत्ता में सुधार होता है, तो हम चित्र में उन मूल्यों को आकर्षित करते हैं जो नेटवर्क हमारे प्रत्येक अंक के लिए 1x1 वर्ग में देगा।

खैर, जैसा कि मेरे लिए, यह एक मामूली परिणाम है, और यह भी 5 प्रयासों में से सबसे अच्छा है, यहां तक कि दो सहमति भी हैं, ऐसे आकारों के नेटवर्क के लिए यह हमेशा संभव नहीं है। एक पंक्ति में 4 और प्रयासों के परिणामों के साथ तस्वीर पर ध्यान दें।

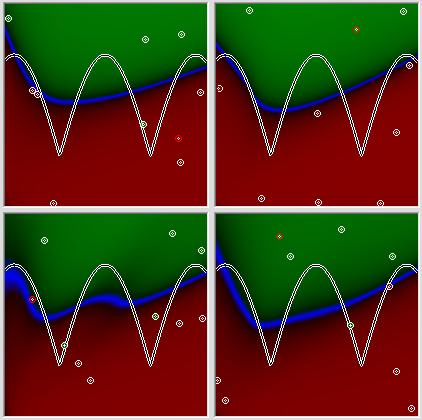
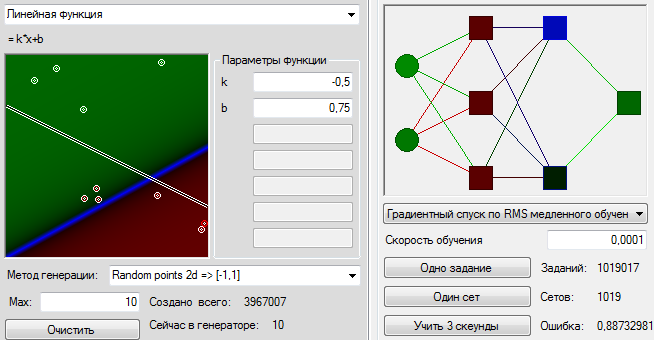
सभी प्रयास, सिद्धांत रूप में, एक समान परिणाम देते हैं, और सभी चित्र बाईं ओर अटे पड़े हैं, इस तथ्य के बावजूद कि इन सभी मामलों में वांछित ग्राफ सममित रूप से स्थित है। नेटवर्क की सुस्ती को कई अलग-अलग कारणों से जिम्मेदार ठहराया जा सकता है, जिसमें प्रोग्रामर के डीएनए में त्रुटियां शामिल हैं, लेकिन यह तथ्य कि नेटवर्क आसानी से बाईं ओर गिर रहा है, कुछ तर्कसंगत स्पष्टीकरण होना चाहिए। तो शायद हमसे कहीं गलती हो गई? आइए एक बहुत ही सामान्य कार्य के साथ सामना करने के लिए नेटवर्क की पेशकश करें - हम एक कार्य के रूप में एक सरल रैखिक संबंध देंगे। हम देखते हैं।

सब ठीक है, सब ठीक है। वैरिएबल की स्थिति को मैन्युअल रूप से ट्रैक करके, आप सत्यापित कर सकते हैं कि एल्गोरिथ्म सही ढंग से काम कर रहा है। तब हम पहेली को केवल थोड़ा और जटिल बनाते हैं। परिणाम निम्न चित्र में देखा जा सकता है।

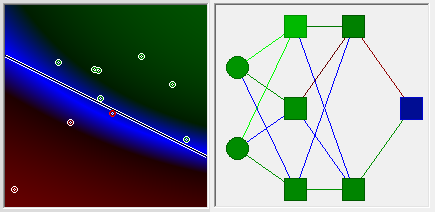
पूरा उपद्रव

यहां हम इसे देखते हैं और समझते हैं कि यहां कुछ गलत है। कार्य इतना सरल नहीं है, यह आदिम है। लेकिन नेटवर्क किसी भी अनुमान में इसके समाधान को खोजने में असमर्थ है।

क्या आपने पहले ही अनुमान लगा लिया है कि क्यों? यह तस्वीर से स्पष्ट रूप से अनुसरण करता है कि यह क्यों असंभव है, लेकिन साथ ही इस सवाल का जवाब है कि पिछली तस्वीर से सभी समाधान बाईं ओर क्यों गिर गए।

यदि हम इस समस्या का समाधान विश्लेषणात्मक रूप से बनाने की कोशिश करते हैं - मैन्युअल रूप से, कलम और कागज के टुकड़े के साथ, तो बहुत जल्दी हम सही उत्तर का सामना करेंगे। यदि आपके पास किसी भी चाल के एक सममित सिग्मोइड के साथ एक न्यूरॉन आपके निपटान में है, तो आप इसे रूपांतरण आउटपुट = k * इनपुट + बी करने के लिए मजबूर नहीं करेंगे। बिंदु (0,0) पर शून्य के संबंध में एक सिग्मॉइड सममित के साथ एक तंत्रिका नेटवर्क कुछ भी आउटपुट नहीं कर सकता है, लेकिन (हेलो, वैसे, रोसेनब्लाट पेसेप्ट्रॉन अभिसरण प्रमेय, ऐसा एक विशेष बिंदु भी है)।

इस समस्या को हल करने के लिए, हम तंत्रिका नेटवर्क में एक और इनपुट जोड़ सकते हैं, और इसे इनपुट डेटा से स्वतंत्र 1 का निरंतर मान दे सकते हैं। और यहां, जैसे कि जादू से, नेटवर्क होशियार हो रहा है और कम से कम संभव समय में और अविश्वसनीय उच्च सटीकता के साथ इससे पहले कार्य सीख रहा है।

और यहीं से मस्ती शुरू होती है।

लेकिन क्या एक अतिरिक्त संदर्भ इनपुट के बिना एक अच्छा सन्निकटन हो सकता है? क्या हम पिछली तस्वीर से नेटवर्क टोपोलॉजी के समाधान के साथ आ सकते हैं? यह पता चला है कि यह संभव है।

उल्टा प्रसार मस्तिष्क

नेटवर्क के पाठ्यक्रम में, मैंने नेटवर्क के लिए मैन्युअल रूप से समाधान खोजने के लिए कई बार सुझाव दिया। अभी, हम इन समाधानों में से एक का विस्तार से विश्लेषण करेंगे।

नेटवर्क इनपुट को S [0] और S [1] कहा जाता है, पहली परत के न्यूरॉन्स A [0] [1], A [0] [2] और A [0] [3] हैं, क्रमशः अगली परत A [1] है। 0] और ए [1] [1] और अंत में, आउटपुट आर [0]। पिछली बार जब हमने समस्या को हल करने की कोशिश की थी, तो हम क्या करेंगे? हमारे पास संदर्भ स्थिरांक का अभाव था। एक न्यूरॉन को लें, उदाहरण के लिए ए [0] [0], और इसके सिनाप्स के लिए बहुत बड़े वजन संलग्न करें, उदाहरण के लिए, 1000। 0 के तत्काल आसपास के क्षेत्र में एक छोटे से क्षेत्र के अलावा, इस न्यूरॉन पर कार्रवाई की क्षमता 1 होगी।

आगे क्या है?एक [0] [1], हम पहले समन्वय के बारे में जानकारी संचारित करेंगे और सिनैप्स वेट १ और ० है, न्यूरॉन ए [०] [२] - दूसरे समन्वय के बारे में जानकारी है, और वजन ० और १ के साथ सिनैप्स हैं। हम चाहते हैं ताकि निर्देशांक के पहले के कार्य की तुलना दूसरे समन्वय के साथ की जा सके। ऐसा करने के लिए, बस दूसरी परत के दूसरे न्यूरॉन में दूसरे समन्वय को स्थानांतरित करें। क्रमशः ०.० और १. सिनैप्स के वज़न को असाइन करें और दूसरी परत के पहले सिनैप्स में, हम मूल्य k * xb प्राप्त करना चाहते हैं। तदनुसार, k = -0.5 b 0.75 के बराबर होगा यदि न्यूरॉन्स के सक्रियण कार्य गायब नहीं हुए। न्यूरॉन A [0] [1] पर इनपुट x = 1 के बारे में केवल 0.76 की क्षमता होगी। तो तुलना के लिए, हमें लगभग b = 0.65 चाहिए। न्यूरॉन A [1] [0] पर इस मान के साथ, लगभग उसी मूल्य को न्यूरॉन A [1] [1] पर प्राप्त किया जाना चाहिए, जो हमारी मूल रेखा पर स्थित बिंदुओं के लिए है। खैर अबइन दो मूल्यों की तुलना करने के लिए, हम आउटपुट न्यूरॉन आर [0] को अन्तर्ग्रथन -1 और 1 के मानों के साथ संपन्न करते हैं। चित्र में हमारे पास जो है वह प्रदर्शित करेगा। सीधी सुंदरता! नीले रंग के नल लगभग मोटे तौर पर हैं जहाँ आपको उनकी आवश्यकता है। ऊपर हरा है। नीचे लाल है। बेशक, अब तक यह पर्याप्त हरा नहीं है और पर्याप्त लाल नहीं है। हालांकि, अन्तर्ग्रथन भार का अंतिम फाइन-ट्यूनिंग त्रुटि वापस प्रसार एल्गोरिथ्म को न केवल बदतर बनाने में सक्षम होगा, बल्कि मुझसे बेहतर होगा। हम एल्गोरिथ्म शुरू करते हैं, और कम संख्या में चरणों के बाद हमारे पास काफी सहनशील सन्निकटन होता है।हालांकि, अन्तर्ग्रथन वेट की अंतिम फाइन-ट्यूनिंग त्रुटि को वापस लाने के लिए एल्गोरिथ्म को न केवल खराब करने में सक्षम होगी, बल्कि मुझसे बेहतर भी होगी। हम एल्गोरिथ्म शुरू करते हैं, और कम संख्या में चरणों के बाद हमारे पास काफी सहनशील सन्निकटन होता है।हालांकि, अन्तर्ग्रथन वेट की अंतिम फाइन-ट्यूनिंग त्रुटि को वापस लाने के लिए एल्गोरिथ्म को न केवल खराब करने में सक्षम होगी, बल्कि मुझसे बेहतर भी होगी। हम एल्गोरिथ्म शुरू करते हैं, और कम संख्या में चरणों के बाद हमारे पास काफी सहनशील सन्निकटन होता है।

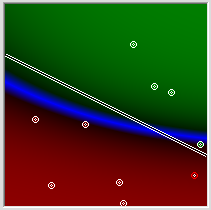
यहां आप देख सकते हैं कि नेटवर्क कैसा दिखता है:

XML जिसके लिए तैयार नेटवर्क निर्यात किया जाता है

 <rumelhart> <input> <SensoryNeuron name="S[0]" potential="0,0396039603960396"/> <SensoryNeuron name="S[1]" potential="0,232673267326733"/> </input> <excitationOrder> <Neuron name="A[0][0]" potential="1"> <synaps weight="999,800400355468" axon="S[0]" potential="39,5960554596225" /> <synaps weight="999,545226476388" axon="S[1]" potential="232,5674536851" /> </Neuron> <Neuron name="A[0][1]" potential="0,116342019068401"> <synaps weight="1,13712492177543" axon="S[0]" potential="0,0450346503673436" /> <synaps weight="0,308744483692756" axon="S[1]" potential="0,0718365877898986" /> </Neuron> <Neuron name="A[0][2]" potential="0,29693700450834"> <synaps weight="-0,0240967983057654" axon="S[0]" potential="-0,000954328645772886" /> <synaps weight="1,31992553337836" axon="S[1]" potential="0,307111386479124" /> </Neuron> <Neuron name="A[1][0]" potential="0,683083451961352"> <synaps weight="1,02404884109051" axon="A[0][0]" potential="1,02404884109051" /> <synaps weight="-0,649771926175146" axon="A[0][1]" potential="-0,0755957778251805" /> <synaps weight="-0,382508459201211" axon="A[0][2]" potential="-0,113580916074308" /> </Neuron> <Neuron name="A[1][1]" potential="0,0324886810522597"> <synaps weight="-0,404744328902586" axon="A[0][0]" potential="-0,404744328902586" /> <synaps weight="0,161865952018599" axon="A[0][1]" potential="0,0188318116762727" /> <synaps weight="1,40909563283595" axon="A[0][2]" potential="0,418412636280091" /> </Neuron> </excitationOrder> <output> <Neuron name="R[0]" potential="-0,707598983150799"> <synaps weight="-1,36308077548559" axon="A[1][0]" potential="-0,931097921420856" /> <synaps weight="1,50019153981243" axon="A[1][1]" potential="0,0487392444542643" /> </Neuron> </output> </rumelhart>

इस सभी मैनुअल समाधान में एक दिलचस्प बिंदु है। तथ्य यह है कि सिद्धांत में, त्रुटि के पीछे प्रसार एल्गोरिथ्म द्वारा संचालित पेसेप्ट्रॉन, हमारी स्थिति में इस समाधान का पता नहीं लगा सका। क्योंकि प्रारंभिक अवस्था के बीच, जब सभी सिनैप्स की रेंज में एक प्रारंभिक मान होता है [-1,1] और अंतिम एक, जिस पर दो सिनैप्स का वजन बहुत अधिक होता है, बहुत ही बुरे निर्णयों से भरा एक बहुत चौड़ा रसातल होता है, और क्रमिक वंश एल्गोरिथ्म ध्यान से नेटवर्क को बाहर धकेल देगा। यह बंद हो जाता है। जैसा कि मैं कहता हूं कि फैसले में उच्च असंगति है। एनीलिंग सिमुलेशन एल्गोरिथ्म गलती से नेटवर्क को उस क्षेत्र में फेंक सकता है, लेकिन इसके लिए एनीलिंग तापमान अधिक होना चाहिए (ताकि नेटवर्क को इतनी दूर फेंकने का मौका मिले) और बहुत जल्दी कम हो जाए ताकि यह तुरंत बाहर न जाए। और फिर भी, चूंकि सिनेप्स के हिस्से का वजन बड़ा होना चाहिए, जबकि अन्य, इसके विपरीत, बहुत कम, अलग-अलग, हमें गलती से न केवल बड़े मूल्यों में मिलना चाहिए, बल्कि दुर्घटना से, छोटे मूल्यों में प्राप्त करना अच्छा है, और एल्गोरिथ्म को बहुत तेजी से फ्रीज करना चाहिए जब कि मुझे ऐसा कुछ मिला क्योंकि उपयुक्त समाधानों का क्षेत्र बहुत संकीर्ण है। 0.0001 की सीखने की गति पर भी, एक साधारण स्टोचस्टिक ढाल वंश आसानी से एक नेटवर्क को बाहर फेंक सकता है। सामान्य तौर पर, वह समाधान है, लेकिन यह सिर्फ अपना नेटवर्क नहीं खोज सकता है।

यद्यपि, जैसा कि आपने शायद देखा है, यदि आप नेटवर्क के निपटान में 30 न्यूरॉन्स की तीन परतें डालते हैं, तो नेटवर्क स्वतंत्र रूप से शून्य बिंदु समस्या को आंशिक रूप से हल करने का एक तरीका खोज सकता है। हालाँकि ऐसा करना उसके लिए बहुत असुविधाजनक है। यदि हम नेटवर्क को एक अतिरिक्त संदर्भ इनपुट देते हैं, तो चित्र एक तरफ से तिरछा होना बंद हो जाता है। लेकिन इससे भी अधिक, एक समाधान खोजने की प्रक्रिया बहुत अधिक उत्पादक बन जाती है - एक निरंतर बनाने के लिए अपने अमूल्य न्यूरॉन्स के आधे खर्च करने की आवश्यकता को समाप्त कर दिया, नेटवर्क पूरी तरह से तैनात करने और कुशलता से व्यवहार करने में सक्षम था जैसे कि इसकी एक परत थी और कई न्यूरॉन्स थे। विवरण तस्वीर में प्रशंसा की जा सकती है।

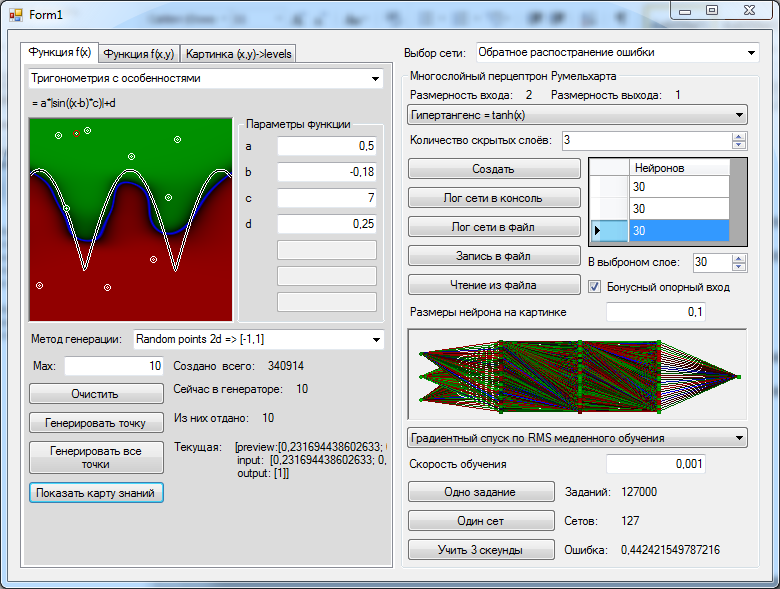
और इस समस्या का समाधान टोपोलॉजी में हेरफेर करके कई बार नेटवर्क प्रशिक्षण की गुणवत्ता में सुधार करने का एकमात्र तरीका नहीं है। मैंने इसे सिर्फ इसलिए दिखाया क्योंकि इसे सबसे सरल उदाहरण का उपयोग करके एक विश्लेषणात्मक समाधान के साथ खूबसूरती से प्रदर्शित किया जा सकता है।

दिलचस्प बात यह है कि निरंतर इनपुट के साथ एक इनपुट जोड़ने से नेटवर्क के प्रदर्शन में भी सुधार होता है जब शून्य का पड़ोस इनपुट कार्य में नहीं आता है जिसके साथ हम नेटवर्क को प्रशिक्षित करते हैं। उदाहरण के लिए, नीचे मैंने एक नियमित नेटवर्क का प्रस्ताव दिया, और एक अतिरिक्त इनपुट के साथ एक नेटवर्क एक ही कार्य और समान रूप से बदलती सीखने की गति। इसके अलावा, पूरे ग्राफ को दोनों अक्षों पर एक-एक करके स्थानांतरित किया गया था, ताकि 1 से 2 तक की रेंज में नेटवर्क इनपुट को मान मिले। परिणाम स्वयं के लिए बोलते हैं।

अंत में, यदि हम इस एल्गोरिथ्म को रोसेनब्लाट पेसेप्ट्रॉन द्वारा प्रस्तावित पहली प्रारंभिक पूर्णांक समस्या को खिलाते हैं, तो परिणाम पिछली बार की तुलना में बेहतर होगा। लेकिन हमें इस तथ्य को भी ध्यान में रखना चाहिए कि 30 न्यूरॉन्स के साथ बहुपरत पर्सेप्ट्रोन में बहुत अधिक सिनेप्स हैं, क्योंकि यह मूल डेटा की तुलना में नेटवर्क डेटा को रिकॉर्ड करने के लिए काफी अधिक बाइट्स लेता है।

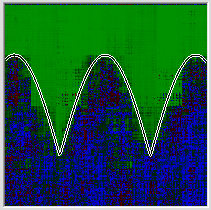
निष्कर्ष

रोसेनब्लट परसेप्ट्रान को केवल ज्ञान दिया जा सकता है जो शून्य इनपुट के साथ एक शून्य आउटपुट मानता है। यदि आप अभिसरण प्रमेय में रुचि रखते थे, लेकिन ध्यान नहीं दिया कि यह इस प्रकार है, तो इसे और अधिक ध्यान से पढ़ें। मैं यह कभी नहीं मानूंगा कि रोसेनब्लट या मिनस्की को सबूतों में गलत माना जा सकता है;
, . , , ;
, . , , , ;
, , . , ;
तथ्य यह है कि समस्या को एक तंत्रिका नेटवर्क की मदद से हल किया जा सकता है, इसका मतलब यह बिल्कुल नहीं है कि यह समाधान नेटवर्क की प्रारंभिक स्थिति से प्राप्त किया जा सकता है। इसके अलावा, निर्णय स्थान की कनेक्टिविटी को तंत्रिका नेटवर्क के प्रशिक्षण में मुख्य कारकों में से एक माना जाना चाहिए;
बहुत सारे मामलों में इनपुट के लिए एक सरल निरंतर मूल्य जोड़ना विभिन्न कार्यों के लिए नेटवर्क की गुणवत्ता में बहुत सुधार करता है।

UPD: कोड में एक बग फिक्स्ड। यह रिवर्स डिस्ट्रीब्यूशन के कार्यान्वयन में महत्वपूर्ण प्रतीत होता है, लेकिन किसी कारण से नेटवर्क के सभी परिणाम नहीं बदले हैं। यह मुझे और भी आश्चर्यचकित करता है।

एक तंत्रिका नेटवर्क के दिमाग में क्या होता है और उनकी मदद कैसे की जाती है

सुविधाजनक कार्य

और बहुपरत रूमेलहार्ट परसेप्ट्रॉन के बारे में क्या?

पूरा उपद्रव

उल्टा प्रसार मस्तिष्क

निष्कर्ष

More articles: