कार्टेशियन ट्री: पार्ट 2. ट्री में मूल्यवान जानकारी और इसके साथ कई ऑपरेशन

सामग्री की तालिका (वर्तमान में)

भाग 1. विवरण, संचालन, अनुप्रयोग।

भाग 2. पेड़ में मूल्यवान जानकारी और इसके साथ कई ऑपरेशन।

भाग 3. निहित कुंजी द्वारा कार्टेशियन पेड़।

जारी रखने के लिए ...

आज के व्याख्यान का विषय

पिछली बार जब हम मिले थे - स्पष्ट रूप से, बहुत मोटे तौर पर - एक कार्टेशियन पेड़ की अवधारणा और इसकी मुख्य कार्यक्षमता से परिचित हो गया। केवल अब तक हमने इसका उपयोग एक अनोखे तरीके से किया है: एक "अर्ध-संतुलित" खोज वृक्ष के रूप में। यही है, हमें कुंजियों की एक सरणी दी जाए, उनके लिए यादृच्छिक रूप से उत्पन्न प्राथमिकताओं को जोड़ें, और एक पेड़ प्राप्त करें जिसमें प्रत्येक कुंजी को लघुगणकीय समय में जोड़ा और जोड़ा जा सके और न्यूनतम प्रयास किया जा सके। अच्छा लगता है, लेकिन पर्याप्त नहीं है।



सौभाग्य से (या दुर्भाग्य से?), वास्तविक जीवन ऐसे trifling कार्यों तक सीमित नहीं है। आज क्या चर्चा होगी। एजेंडा पर पहला सवाल तथाकथित के-थ ऑर्डिनल आँकड़े है, या एक पेड़ में एक सूचकांक है जो आसानी से हमें कोने में उपयोगकर्ता की जानकारी संग्रहीत करने के लिए ले जाएगा, और अंत में, अनगिनत जोड़तोड़ के लिए जो इस जानकारी के साथ प्रदर्शन करने की आवश्यकता हो सकती है। चलो चलते हैं।

हम एक इंडेक्स की तलाश कर रहे हैं

गणित में, केथ ऑर्डिनल स्टेटिस्टिक एक रैंडम वैरिएबल है, जो प्रायिकता स्पेस से रैंडम सैंपल के Kth सबसे बड़े एलिमेंट से मेल खाता है। बहुत होशियार। आइए पेड़ पर वापस जाएं: हर समय हमारे पास एक कार्टेशियन पेड़ है, जो कि इसके प्रारंभिक निर्माण के क्षण से पहले से ही काफी बदल सकता है। हमें आरोही क्रम में इस पेड़ की Kth कुंजी बहुत जल्दी खोजने की आवश्यकता है - वास्तव में, यदि हम अपने पेड़ को लगातार बनाए गए क्रमबद्ध सरणी के रूप में प्रस्तुत करते हैं, तो यह केवल सूचकांक K के तहत तत्व तक पहुंच है। पहली नज़र में, यह बहुत स्पष्ट नहीं है कि इसे कैसे व्यवस्थित किया जाए: हमारे पेड़ एन में चाबियाँ, और वे किसी भी तरह संरचना में बिखरे हुए हैं।









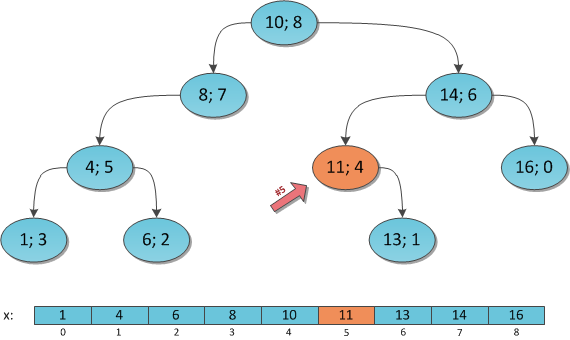
हालांकि, स्पष्ट रूप से, किसी भी तरह से नहीं। हम खोज पेड़ की संपत्ति को जानते हैं - प्रत्येक शीर्ष के लिए इसकी कुंजी इसके बाएं सबट्री की सभी कुंजियों से बड़ी है, और सही सबट्री की सभी कुंजियों से कम है। इसलिए, क्रमबद्ध क्रम में पेड़ की चाबियों की व्यवस्था करने के लिए, उस पर तथाकथित इन-ऑर्डर ट्रैवर्सल को ले जाने के लिए पर्याप्त है, अर्थात्, पूरे पेड़ के माध्यम से जाओ, "पहले बाएं उप-क्रमिक बायपास के सिद्धांत को पूरा करते हुए, फिर रूट की कुंजी, और फिर सही उपशीर्षक पुनरावृत्ति"। यदि इस तरह से सामना की गई प्रत्येक कुंजी एक सूची में दर्ज की गई है, तो अंत में हम पेड़ के सभी कोने की पूरी तरह से क्रमबद्ध सूची प्राप्त करेंगे। जो कोई भी विश्वास नहीं करता है वह आंकड़ा से व्युत्पन्न प्रक्रिया को आंकड़े से थोड़ा अधिक ले जा सकता है - वह उसी आकृति से एक सरणी प्राप्त करेगा।

उपर्युक्त तर्क हमें कार्टेशियन पेड़ के लिए एक पुनरावृत्ति लिखने की अनुमति देता है, ताकि भाषा के मानक साधनों ( foreach



, आदि) के द्वारा, हम आरोही क्रम में इसके तत्वों के माध्यम से जाएंगे। C # में, आप बस एक इन-ऑर्डर ट्रैवर्सल फ़ंक्शन लिख सकते हैं और yield return



ऑपरेटर का उपयोग कर सकते yield return



, और उन में जहां ऐसी कोई शक्तिशाली विशेषता नहीं है, आपको दो तरीकों में से एक पर जाना होगा। या प्रत्येक शीर्ष पर पेड़ में "अगले" तत्व के लिए एक लिंक स्टोर करें, जो मूल्यवान स्मृति का एक अतिरिक्त खर्च देता है। या अपने स्वयं के स्टैक के माध्यम से एक गैर-पुनरावर्ती पेड़ ट्रैवर्सल लिखना, जो कुछ हद तक अधिक कठिन है, लेकिन यह कार्यक्रम की गति और स्मृति लागत दोनों में सुधार करेगा।

बेशक, इस तरह के दृष्टिकोण समस्या के पूर्ण समाधान के रूप में विचार करने के लायक नहीं है, क्योंकि इसके लिए ओ (एन) समय की आवश्यकता होती है, और यह अस्वीकार्य है। लेकिन आप इसे बेहतर बनाने की कोशिश कर सकते हैं, अगर हमें तुरंत पता चल जाए कि पेड़ के किन हिस्सों में जाने लायक नहीं है, क्योंकि बड़े या छोटे तत्वों की गारंटी है। और यह पहले से ही महसूस करना काफी संभव है, अगर हम पेड़ के प्रत्येक शीर्ष के लिए याद करते हैं कि एक पुनरावर्ती प्रवेश के दौरान हमें कितने तत्वों को प्राप्त करना होगा। यही है, हम प्रत्येक शीर्ष पर इसके उप आकार का संग्रह करेंगे।



आंकड़ा प्रत्येक शीर्ष पर चिपकाए गए उपशीर्षक के आकार के साथ एक ही पेड़ को दर्शाता है।







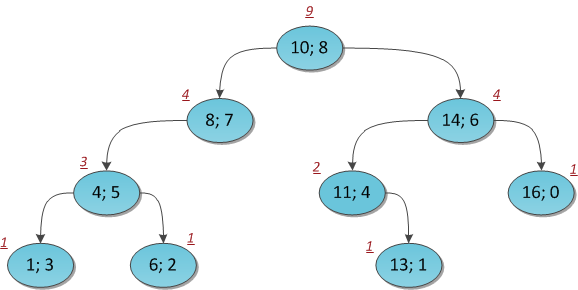
फिर मान लीजिए कि हमने ईमानदारी से प्रत्येक उपशीर्षक में कोने की संख्या की गणना की। अब हम शून्य (!) से शुरू होने वाले अनुक्रमण में Kth तत्व को खोजते हैं।



एल्गोरिथ्म स्पष्ट है: हम पेड़ की जड़ को देखते हैं और इसके बाएं सबट्री एस _एल के आकार पर, दाईं ओर के आकार की भी आवश्यकता नहीं है।

यदि एस _एल = के, तो हमें आवश्यक तत्व मिला, और यह जड़ है।

यदि एस _एल > के, तो वांछित तत्व कहीं बाएं सबट्री में है, वहां नीचे जाएं और प्रक्रिया को दोहराएं।

यदि एस _एल <के, तो वांछित तत्व कहीं सही उपप्रकार में है। सही पर उपप्रकारों के आकारों का सही उत्तर देने के लिए, और सही उपप्रकार के लिए प्रक्रिया को दोहराने के लिए S S _L +1 द्वारा K को कम करें।



मैं इस खोज को उसी पेड़ पर K = 6 के लिए मॉडल करूंगा:

शीर्ष (10; 8), एस _एल = 4, के = 6. हम दाईं ओर जाते हैं, कश्मीर को 4 + 1 = 5 से कम करते हैं।

शीर्ष (14; 6), S _L = 2, K = 1. हम K को बदले बिना बाएं चलते हैं।

शीर्ष (11; 4), एस _एल = 0 (कोई बाएं बेटा नहीं), के = 1. हम दाईं ओर जाते हैं, कश्मीर को 0 + 1 = 1 से घटाते हैं।

शीर्ष (13; 1), एस _एल = 0 (कोई बाएं बेटा नहीं), के = 0. कुंजी मिली है।

उत्तर: कार्टेशियन वृक्ष में सूचकांक 6 के अंतर्गत कुंजी 13 है।



इस मार्ग के सभी, सिद्धांत रूप में, द्विआधारी खोज पेड़ में एक साधारण कुंजी खोज के समान है - हम बस पेड़ के नीचे जाते हैं, वर्तमान शीर्ष पर पैरामीटर के साथ वांछित पैरामीटर की तुलना करते हैं, और स्थिति के आधार पर, बाएं या दाएं मुड़ें। मैं पहले से कहूंगा - हम एक ही समय में विभिन्न एल्गोरिदम में एक जैसी स्थिति के साथ मिलेंगे, यह विभिन्न बाइनरी पेड़ों के लिए पूरी तरह से विशिष्ट है। ट्रैवर्सल एल्गोरिथ्म इतना विशिष्ट है कि यह आसानी से अस्थायी है। जैसा कि आप देख सकते हैं, यहां पुनरावृत्ति की भी आवश्यकता नहीं है, हम प्रत्येक पुनरावृत्ति के साथ बदलते हुए कुछ चर के साथ एक सरल चक्र के साथ कर सकते हैं।

एक कार्यात्मक भाषा में, आप पुनरावृत्ति के माध्यम से एक समाधान लिख सकते हैं, और यह प्रदर्शन में एक बूंद खोने के बिना, बहुत अधिक खूबसूरती से दिखेगा और पढ़ेगा: पुनरावृत्ति पूंछ-आधारित है, और संकलक तुरंत उसी सामान्य लूप में इसे अनुकूलित करेंगे। उन लोगों के लिए जो कार्यात्मक प्रोग्रामिंग जानते हैं, लेकिन मेरे शब्दों में संदेह है - हास्केल कोड:

data Ord a => Treap a = Null

| Node { key :: a , priority :: Int , size :: Int , left :: (Treap a) , right :: (Treap a) }



sizeOf :: ( Ord a) => Treap a -> Int

sizeOf Null = 0

sizeOf Node {size = s} = s



kthElement :: ( Ord a) => (Treap a) -> Int -> Maybe a

kthElement Null _ = Nothing

kthElement (Node key _ _ left right) k

| sizeLeft == k = Just key

| sizeLeft < k = kthElement left k

| sizeLeft > k = kthElement right (k - sizeLeft - 1)

where sizeLeft = sizeOf left



प्रदर्शन की बात कही। Kth तत्व का खोज निष्पादन समय स्पष्ट रूप से O (लॉग ₂ N) है, क्योंकि हम बस पेड़ के ऊपर से नीचे की ओर गए थे।



पाठकों को अपमानित न करने के लिए, कार्यात्मक के अलावा, मैं C # में पारंपरिक स्रोत कोड का भी हवाला दूंगा। इसमें, Treap



वर्ग के मानक Treap



में, पहले भाग में दिखाया गया है, एक और पूर्णांक फ़ील्ड Size



जोड़ा गया है - सबट्री का आकार, साथ ही इसे प्राप्त करने के लिए उपयोगी SizeOf



फ़ंक्शन।

 public static int SizeOf(Treap treap) { return treap == null ? 0 : treap.Size; } public int? KthElement(int K) { Treap cur = this; while (cur != null) { int sizeLeft = SizeOf(cur.Left); if (sizeLeft == K) return cur.x; cur = sizeLeft > K ? cur.Left : cur.Right; if (sizeLeft < K) K -= sizeLeft + 1; } return null; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

प्रमुख मुद्दा अभी भी यह तथ्य है कि हम अभी भी नहीं जानते कि पेड़ में सही size



मूल्यों को कैसे बनाए रखा जाए। आखिरकार, पेड़ के लिए एक नई कुंजी के पहले जोड़ के बाद, ये सभी संख्याएं धूल में चली जाएंगी, और उन्हें हर बार फिर से मिलाने के लिए - ओ (एन)! हालाँकि, नहीं। ओ (एन) यह कुछ ऑपरेशन के बाद ले जाएगा जिसने पेड़ को अतुलनीय निर्माण की संरचना में पूरी तरह से बदल दिया। और यहां एक कुंजी का जोड़ है जो अधिक सटीक रूप से कार्य करता है और पूरे पेड़ को नहीं छूता है, लेकिन इसका केवल एक छोटा सा हिस्सा है। तो आप कम रक्त से प्राप्त कर सकते हैं।



जैसा कि आपको याद है, सब कुछ आपके साथ किया जाता है, इसलिए बोलने के लिए, स्प्लिट और मर्ज के माध्यम से। यदि आप पेड़ में अतिरिक्त जानकारी का समर्थन करने के लिए इन दो मुख्य कार्यों को अनुकूलित करते हैं - इस मामले में, उपप्रकारों का आकार - तो अन्य सभी ऑपरेशन स्वचालित रूप से सही ढंग से किए जाएंगे, क्योंकि वे पेड़ में अपना परिवर्तन नहीं करते हैं (केवल एक शीर्ष से प्राथमिक पेड़ बनाने के लिए जिसमें Size



आवश्यकता होती है) डिफ़ॉल्ट को 1 पर सेट करना न भूलें!)।

मैं मर्ज ऑपरेशन को संशोधित करके शुरू करूंगा।



मर्ज निष्पादन दिनचर्या को याद करें। उसने पहले नए पेड़ के लिए जड़ का चयन किया, और फिर पुन: अपने एक पेड़ के साथ दूसरे पेड़ में विलय कर दिया और हटाए गए उपशीर्षक के स्थान पर परिणाम लिख दिया। मैं उस मामले का विश्लेषण करूंगा जब सही उपप्रकार को मर्ज करना आवश्यक था, दूसरा सममित है। पिछली बार की तरह, पुनरावृत्ति हमें बहुत मदद करेगी।



हम प्रेरण परिकल्पना करते हैं: मर्ज को उपप्रकार पर निष्पादित होने के बाद भी, सब कुछ पहले से ही सही ढंग से उन में गणना की जाती है। फिर हमारे पास निम्नलिखित चीजें हैं: बाएं सबट्री में, आयामों की सही गणना की जाती है, क्योंकि किसी ने उसे छुआ नहीं; सही में भी सही ढंग से गणना कर रहे हैं, क्योंकि यह मर्ज का नतीजा है। पुनर्स्थापना न्याय केवल नए पेड़ के बहुत मूल में रहता है! ठीक है, बस अंत से पहले इसे पुनः size = left.size + right.size + 1



( size = left.size + right.size + 1



) , और अब मर्ज ने पूरी तरह से एक नया पेड़ बनाया है, जिसके प्रत्येक शीर्ष पर सही उप-आकार है।



मर्ज का स्रोत कोड थोड़ा बदल जाएगा: जवाब वापस करने से पहले पुनर्गणना रेखा पर। वह एक टिप्पणी द्वारा चिह्नित है।

 public void Recalc() { Size = SizeOf(Left) + SizeOf(Right) + 1; } public static Treap Merge(Treap L, Treap R) { if (L == null) return R; if (R == null) return L; Treap answer; if (Ly > Ry) { var newR = Merge(L.Right, R); answer = new Treap(Lx, Ly, L.Left, newR); } else { var newL = Merge(L, R.Left); answer = new Treap(Rx, Ry, newL, R.Right); } answer.Recalc(); // ! return answer; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ठीक यही स्थिति स्प्लिट ऑपरेशन के साथ हमारी प्रतीक्षा करती है, जो एक पुनरावर्ती कॉल पर भी आधारित है। मैं आपको याद दिलाता हूं: यहां, पेड़ की जड़ में कुंजी के मूल्य के आधार पर, हमने निर्दिष्ट कुंजी द्वारा मूल एक के बाएं या दाएं उपप्रकार को विभाजित किया है, और परिणामों में से एक को वापस निलंबित कर दिया गया था, और दूसरा अलग से वापस किया गया था। फिर से, यहां तक ​​कि स्पष्टता के लिए, हम पुन: टी। राइट को विभाजित करते हैं।



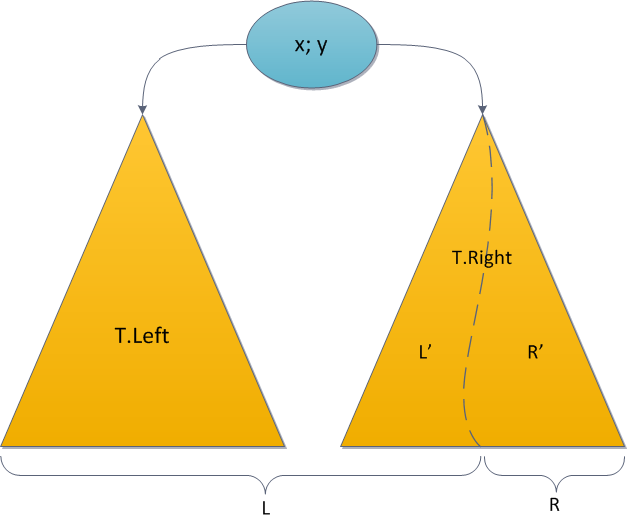
परिचित प्रेरण परिकल्पना - स्प्लिट के पुनरावर्ती कॉल सब कुछ सही ढंग से गणना करते हैं - इस बार भी हमारी मदद करेंगे। फिर टी.लिफ्ट में आयाम सही हैं - किसी ने उन्हें छुआ नहीं; L 'में आयाम सही हैं - यह स्प्लिट का बायाँ परिणाम है; R 'में आयाम सही हैं - यह सही स्प्लिट परिणाम है। पूरा करने से पहले, आपको भविष्य के पेड़ एल की जड़ (x; y) पर न्याय को बहाल करने की आवश्यकता है और जवाब तैयार है।



नई स्प्लिट का स्रोत कोड, जिसमें दो वर्धित लाइनें संस्करण के आधार पर, L या R के रूट में Size



वैल्यू को रिकवर करती हैं।

 public void Recalc() { Size = SizeOf(Left) + SizeOf(Right) + 1; } public void Split(int x, out Treap L, out Treap R) { Treap newTree = null; if (this.x <= x) { if (Right == null) R = null; else Right.Split(x, out newTree, out R); L = new Treap(this.x, y, Left, newTree); L.Recalc(); //   L! } else { if (Left == null) L = null; else Left.Split(x, out L, out newTree); R = new Treap(this.x, y, newTree, Right); R.Recalc(); //   R! } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

चर्चा की गई "न्याय की बहाली" - शीर्ष पर मूल्य का पुनर्गणना - मैंने एक अलग फ़ंक्शन के रूप में एकल किया। यह मूल रेखा है जिस पर पूरे कार्टेशियन वृक्ष की कार्यक्षमता टिकी हुई है। और जब लेख के दूसरे भाग में हम कई अलग-अलग ऑपरेशनों के माध्यम से जाएंगे, प्रत्येक अपने स्वयं के "रिकवरी" के साथ, तो इसे पूरे क्लास कोड की तुलना में एक ही स्थान पर बदलना अधिक सुविधाजनक होगा। इस तरह के फ़ंक्शन में एक सामान्य संपत्ति होती है: यह मानता है कि बाएं बेटे में सब कुछ उचित है, सही बेटे में सब कुछ उचित है, और इन आंकड़ों के आधार पर यह रूट में पैरामीटर को पुनर्गणना करता है। इस प्रकार, किसी भी अतिरिक्त मापदंडों का समर्थन करना संभव है जो कि वंशजों से गणना की जाती है, उपप्रकार के आकार केवल एक विशेष उदाहरण हैं।

वास्तविक दुनिया में आपका स्वागत है

चलिए असल जिंदगी में लौटते हैं। इसमें, डेटा को एक पेड़ में संग्रहीत किया जाना है जो केवल एक कुंजी तक सीमित नहीं है। और इस डेटा के साथ लगातार किसी तरह का हेरफेर करना पड़ता है। उदाहरण के लिए, इस लेख में मैं स्पिरिट Cost



ऐसे नए क्षेत्र का नाम दूंगा।



तो, आइए हमेशा कुंजियों को प्राप्त करें (और कभी-कभी हटाएं), और उनमें से प्रत्येक की एक समान कीमत है - Cost



। और आपको इस सभी गड़बड़ में अधिकतम कीमत पर तेजी से अनुरोधों का समर्थन करने की आवश्यकता है। आप पूरी संरचना में अधिकतम पूछ सकते हैं, लेकिन केवल इसके कुछ उप-खंड में: कहते हैं, उपयोगकर्ता को 2007 के लिए अधिकतम कीमत में दिलचस्पी हो सकती है (यदि चाबियाँ समय से संबंधित हैं, तो इस तरह के तत्वों के एक सेट पर अधिकतम मूल्य के अनुरोध के रूप में व्याख्या की जा सकती है, जहां A एक्स < बी )।



यह मुश्किल नहीं है, क्योंकि अधिकतम भी "बहाल न्याय" समारोह के लिए एक उम्मीदवार के रूप में पूरी तरह से फिट बैठता है। बस इस तरह लिखें:

 public double Cost; //  public double MaxTreeCost; public static double CostOf(Treap treap) { return treap == null ? double.NegativeInfinity : treap.MaxTreeCost; } public void Recalc() { MaxTreeCost = Math.Max(Cost, Math.Max(CostOf(Left), CostOf(Right))); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

यही स्थिति न्यूनतम के साथ है, और योग के साथ, और तत्व के कुछ बूलियन विशेषताओं के साथ (तथाकथित "रंग" या "अंकन")। उदाहरण के लिए:

 //  public double SumTreeCost; public static double CostOf(Treap treap) { return treap == null ? 0 : treap.SumTreeCost; } public void Recalc() { SumTreeCost = Cost + CostOf(Left) + CostOf(Right); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

या:

 public bool Marked; //  public bool TreeHasMarked; public static bool MarkedOf(Treap treap) { return treap == null ? false : treap.TreeHasMarked; } public void Recalc() { TreeHasMarked = Marked || MarkedOf(Left) || MarkedOf(Right); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

इस तरह के मामलों में याद रखने वाली एकमात्र बात यह है कि नए अलग-अलग कोने बनाते समय इन मापदंडों को निर्माणकर्ता में शुरू करना है।

जैसा कि वे एक कार्यात्मक दुनिया में कहेंगे, आप और मैं किसी तरह के पेड़ को मोड़ रहे हैं ।

इस प्रकार, हम पूरे पेड़ के लिए पैरामीटर के मूल्य का अनुरोध कर सकते हैं - यह रूट में संग्रहीत है। यदि हम फिर से एक द्विआधारी खोज पेड़ की संपत्ति को याद करते हैं, तो अवज्ञा पर क्वेरी भी मुश्किल नहीं है। प्रत्येक वर्टेक्स की कुंजी बाईं सबट्री की सभी कुंजियों से बड़ी होती है और दाएं सबट्री की सभी कुंजियों से कम होती है। इसलिए, हम वस्तुतः यह मान सकते हैं कि प्रत्येक शीर्ष कुंजी के कुछ अंतराल के साथ जुड़ा हुआ है जो सैद्धांतिक रूप से इसमें और इसके उपप्रकार में हो सकता है। तो, रूट पर यह अंतराल (-+; + , ) है , उनके बाएं बेटे पर (-x; x) , दाईं ओर - (x; + ∞) , जहां x रूट में प्रमुख मूल्य है। सभी अंतराल दोनों तरफ से खुले हैं, एक्स को सही सबट्री की कुंजियों के बीच नहीं पाया जा सकता है। यदि आप पेड़ में समान कुंजियों की अनुमति देते हैं और, पहले भाग के रूप में, तुलनित्र को उन सभी को एक ही सबट्री में फेंक देते हैं - कहते हैं, बाएं एक में - तो बाएं बेटे के लिए अंतराल (-∞; x] हो जाएगा।



स्पष्टता के लिए, मैं पहले से ही जांच किए गए कार्टेशियन पेड़ के प्रत्येक शीर्ष के लिए इसी अंतराल को दिखाऊंगा।







अब यह स्पष्ट है कि शीर्ष में संग्रहीत पैरामीटर इस शीर्ष के अंतराल पर संपूर्ण कुंजी के लिए संबंधित विशेषता (अधिकतम, योग, आदि) के मूल्य के लिए जिम्मेदार है।



और हम अंतराल पर अनुरोधों का जवाब दे सकते हैं [ए; बी) (सी ++ में और इसी तरह की भाषाओं में आमतौर पर आधे-खुले अंतराल के साथ काम करना अधिक सुविधाजनक होता है जिसमें बाएं छोर शामिल होता है और सही एक को शामिल नहीं करता है; भविष्य में मैं ऐसा करूंगा)।

खंडों के वृक्ष से परिचित कोई व्यक्ति यह सोच सकता है कि यह एक ही पुनरावर्ती वंश को लागू करने के लायक है, धीरे-धीरे वर्तमान शीर्ष को स्थानीय बनाना जो पूरी तरह से वांछित अंतराल या उसके टुकड़े से मेल खाती है। लेकिन हम इसे आसान और तेज़ी से करेंगे, जिससे कार्य पिछले एक तक कम हो जाएगा।



कैंची के मालिक, हम पहले पेड़ को कुंजी A-1 से विभाजित करेंगे। सही स्प्लिट परिणाम, जो ए की तुलना में अधिक या बराबर सभी कुंजियों को संग्रहीत करता है, को फिर से विभाजित किया जाता है - इस बार कुंजी बी द्वारा। बीच में, हमें सभी तत्वों के साथ एक पेड़ मिलता है जिसके लिए चाबियाँ वांछित अंतराल से संबंधित होती हैं। एक पैरामीटर का पता लगाने के लिए, बस रूट में इसके मूल्य को देखें - आखिरकार, स्प्लिट फ़ंक्शन ने हमारे लिए प्रत्येक पेड़ के लिए न्याय बहाल करने के लिए पहले से ही सभी काले काम किए हैं :)



क्वेरी रन समय स्पष्ट रूप से O (लॉग ₂ एन) है: दो स्प्लिट निष्पादन। अधिकतम के लिए स्रोत कोड:

 public double MaxCostOn(int A, int B) { Treap l, m, r; this.Split(A - 1, out l, out r); r.Split(B, out m, out r); return CostOf(m); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

आस्थगित कंप्यूटिंग की शक्ति

आज के एरोबेटिक्स एक पेड़ के जीवन के दौरान उपयोगकर्ता की जानकारी को बदलने की क्षमता है। यह स्पष्ट है कि कुछ शीर्ष पर Cost



के मूल्य को बदलने के बाद, हमारे सभी पिछले पैरामीटर जो उनके उपप्रकार में मूल्यों के लिए संचित उत्तर हैं, अब मान्य नहीं हैं। आप निश्चित रूप से पूरे पेड़ के माध्यम से जा सकते हैं और उन्हें फिर से भर सकते हैं, लेकिन यह ओ (एन) फिर से है, और किसी भी द्वार में नहीं चढ़ता है। क्या करें?



अगर हम Cost



इन ए सिंगल पीक में एक साधारण बदलाव के बारे में बात कर रहे हैं, तो यह ऐसी समस्या नहीं है। सबसे पहले, हम, ऊपर से नीचे की ओर बढ़ रहे हैं, वांछित तत्व पाते हैं। हम इसमें जानकारी बदलते हैं। और फिर, नीचे से जड़ तक वापस जाने पर, हम बस मानक फ़ंक्शन के साथ पैरामीटर मानों को पुनर्गणना करते हैं - आखिरकार, यह परिवर्तन किसी भी अन्य उपप्रकारों को प्रभावित नहीं करेगा, सिवाय इसके कि हम रूट से शीर्ष तक के मार्ग पर गए थे। मेरा मानना ​​है कि स्रोत कोड बहुत मायने नहीं रखता है, कार्य तुच्छ है: इसे कम से कम पुनरावृत्ति के साथ हल करें, कम से कम दो चक्र, रनटाइम अभी भी ओ (लॉग ₂ एन) है।



यदि आप कई कार्यों का समर्थन करने की आवश्यकता है, तो जीवन बहुत अधिक मजेदार हो जाता है। हमारे पास कार्टेशियन ट्री है, इसके प्रत्येक कोने में उपयोगकर्ता की जानकारी Cost



। और हम पेड़ में प्रत्येक Cost



मूल्य में एक ही संख्या ए जोड़ना चाहते हैं (या उपशीर्षक - अंतराल के बारे में चर्चा देखें)। यह एक बहुक्रिया का एक उदाहरण है, इस मामले में एक खंड पर एक निरंतरता जोड़ रहा है। और यहाँ आप रूट के लिए एक सरल मार्ग के साथ नहीं कर सकते।



आइए प्रत्येक शीर्ष पर एक अतिरिक्त पैरामीटर प्राप्त करें, इसे Add



। इसका सार इस प्रकार है: यह संकेत देगा कि किसी दिए गए शीर्ष से बढ़ने वाले पूरे उपशीर्षक को एक स्थिरांक जोड़ना है जो ऐड में निहित है। इसके परिणामस्वरूप देरी होती है: यदि आपको ए में उप-मूल्यों को बदलने की आवश्यकता है, तो हम इस रूटरी में केवल रूट Add



को बदलते हैं, जैसे कि वंशजों को एक वादा देते हैं कि "भविष्य में कभी-कभी, आप सभी के पास एक अतिरिक्त अतिरिक्त होना चाहिए, लेकिन हम वास्तव में इसे करेंगे।" जब तक हमें इसकी आवश्यकता नहीं है, तब तक हम नहीं जीतेंगे।



फिर पेड़ की जड़ से Cost



अनुरोध को एक और अतिरिक्त कार्रवाई करनी होगी, जड़ को Cost



जोड़ना, और परिणामस्वरूप Cost



का वास्तविक Cost



रूप में मूल्यांकन करना, जैसे कि पेड़ की जड़ में झूठ बोलना। अतिरिक्त मापदंडों के लिए अनुरोध के साथ एक ही बात, उदाहरण के लिए, पेड़ में कीमतों का योग: हमारे पास रूट में एक सही ढंग से (!) SumTreeCost



मान है, जो पेड़ के सभी तत्वों के योग को संग्रहीत करता है, लेकिन इस तथ्य को ध्यान में नहीं रखते हुए कि हम इन सभी तत्वों में कुछ जोड़ना चाहते हैं। Add



। सही मायने में सही मूल्य प्राप्त करने के लिए, सभी लंबित परिचालनों को ध्यान में रखते हुए, यह Size



गुणा मूल्य को जोड़ने के लिए पर्याप्त है - SumTreeCost



को सबट्री में तत्वों की संख्या।



यह अभी भी बहुत स्पष्ट नहीं है कि कार्टेशियन पेड़ के विभाजन के साथ क्या करना है - स्प्लिट और मर्ज - और जब हमें अभी भी वादे को पूरा करने और वंशजों को जोड़ने के वादे को जोड़ने की आवश्यकता है। अब मैं इन मुद्दों पर विचार करूंगा।



स्प्लिट ऑपरेशन फिर से समझें। चूंकि मूल पेड़ दो नए लोगों में विभाजित है, और हम मूल एक को खो देते हैं, इसलिए देरी के अलावा आंशिक रूप से प्रदर्शन करना होगा। अर्थात्: पुनरावर्ती कॉल स्प्लिट को T.ight के सही उप-भाग में विभाजित करें। फिर हम इस तरह के फेरबदल करेंगे:



• वादे को जड़ में रखें, जड़ का मूल्य Add



जड़ Cost



Add



।

  T.Cost + = T.Add; 

• लेफ्ट के वादे को "कम" करें: Add



भी पूरे लेफ्ट सबट्री पर निर्भर करता है। लेकिन चूंकि पुनरावृत्ति बाईं ओर नहीं जाती है, इसलिए हमें इस उपप्रकार को सक्रिय रूप से छूने की आवश्यकता नहीं है। बस एक वादा करो।

  T.Left.Add + = T.Add; 

• "चलो" सही करने के लिए वादा करता हूं: संपूर्ण राइट सबट्री के लिए Add



भी आवश्यक है। इसे पुनरावर्ती कॉल से पहले किया जाना चाहिए, ताकि स्प्लिट ऑपरेशन सही कार्टेशियन ट्री को हेरफेर कर सके। पुनरावृत्ति स्वयं एक और अद्यतन करेगा।

  T.Right.Add + = T.Add; 

• हम सेट पुनरावर्ती कॉल करते हैं। स्प्लिट ने हमारे लिए दो सही कार्टेशियन पेड़ दिए।

• चूंकि हमने ईमानदारी से मूल में वादे को पूरा किया, और ईमानदारी से वादे के लिए नीचे लिखा, रूट Add



को रीसेट किया जाना चाहिए।

  T.Add = 0; 

स्प्लिट में सबट्रेसेस के आगे लगाव हमेशा की तरह किया जाता है। नतीजतन, वादों की प्रासंगिक जानकारी के साथ दो सही कार्टेशियन पेड़ हैं: कहीं पूरा, कहीं केवल स्थगित, लेकिन प्रासंगिक।



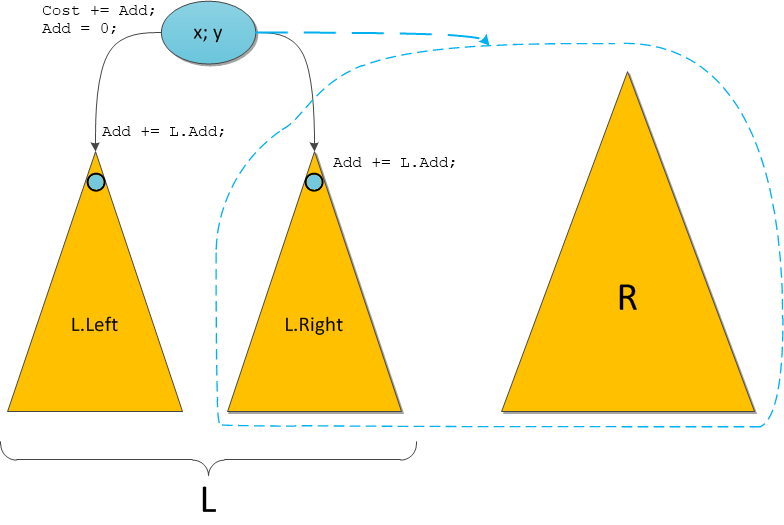
सभी ऑपरेशन नए स्प्लिट डायग्राम पर इंगित किए गए हैं।



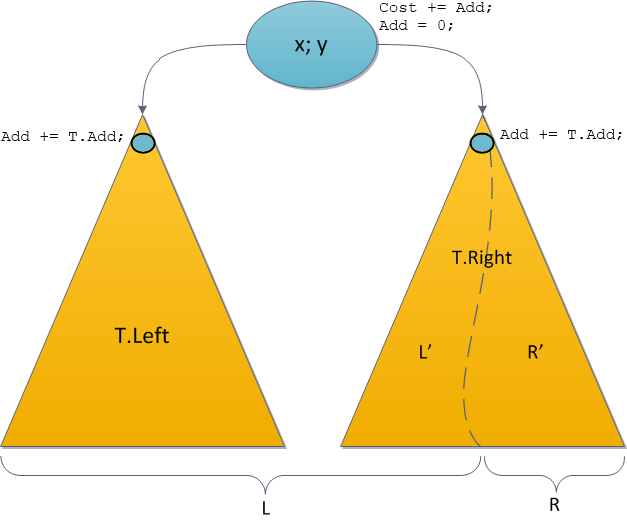
ध्यान दें कि वास्तविक अपडेट केवल उन सिरों पर किए जाते हैं जिनके साथ स्प्लिट ऑपरेशन पुनरावर्ती रूप से चलेगा, बाकी के लिए, सबसे अच्छा, हम वादा थोड़ा कम करेंगे। यही स्थिति मर्ज के साथ होगी।



नया मर्ज मूल रूप से वही करता है। इसे पुन: सही इनपुट ट्री R के साथ L.Right के सही सबट्री को मर्ज करने की आवश्यकता है। फिर हम निम्नलिखित कार्य करते हैं:



• वचन को मूल L में रखो।

  एल। लागत + = एल। जोड़ें; 

• "चलो" एल के वंशजों से वादा करता हूँ - भविष्य के लिए।

  L.Left.Add + = L.Add;
   L.Right.Add + = L.Add; 

• वादा मौलिक रूप से पूरा हुआ है - आप इसके बारे में भूल सकते हैं।

  एल.एड = 0; 

• हम मर्ज (L.Right, R) के लिए आवश्यक पुनरावर्ती कॉल करते हैं, क्योंकि अब इसके दोनों तर्क सही कार्टियन वृक्ष हैं। और वह हमें सही पेड़ भी लौटाएगा।

• हम पहले की तरह, सही बेटे के साथ लौटे पेड़ को लटकाते हैं। परिणामस्वरूप - वादों पर प्रासंगिक जानकारी के साथ फिर से एक कार्टेशियन पेड़।







अब जब हम पूरे पेड़ पर जड़ और परिवर्तन में प्रश्न करने में सक्षम हैं, तो उप-खंडों के लिए इस समाधान को स्केल करना मुश्किल नहीं है, बस उसी सिद्धांत को ऊपर के कुछ पैराग्राफ में लागू करना है।

हम स्प्लिट में दो कॉल करते हैं, एक अलग पेड़ में आवश्यक कुंजी अंतराल के अनुरूप सबट्री का चयन करते हैं।

Add



. .

Merge



. , - .

:)

Recalc



. , .

, , , . «» — , — Cost



, , . — (1) , , Merge Split. , , , .

सारांश

, , , , . , , , , - .



, . « ».



.