Cryptosystems Protocols: Diffie — Hellman, El-Gamal, MTI / A (0), STS

Like the creators of the three-pass protocols from the previous section , the authors of the following algorithms considered them not just mathematical constructions that provided some elementary operation (for example, public key encryption), but tried to build a complete key distribution system around one or two formulas. Some of these constructions, which have been transformed, are used to date (for example, the Diffie-Hellman protocol), some of them remain only in the history of cryptography and information protection.



Later in the 1990s, mathematical asymmetric primitives (encryption and electronic signature) and protocols will be separated, these primitives will be used, which will be demonstrated in the section on asymmetric protocols.

Diffie — Hellman Protocol

The first public key algorithm was proposed by Diffie and Hellman in 1976, “New Directions in Cryptography” ( Bailey Whitfield Diffie, Martin Edward Hellman, “New directions in cryptography” , [Diffie, Hellman 1976] ). This protocol, which can also be called the Diffie-Hellman scheme , was the first to reduce the requirements for the communication channel to establish a secure connection without first exchanging keys.



The protocol allows two parties to create a common session key using a communication channel that an attacker can listen to, but on the assumption that the latter cannot change the message content.



Let $$$p$ - a large prime number $$$g$ - a primitive element of the group $$$\ mathbb {Z} _p ^ *$ , $$$y = g ^ x \ bmod p$ , and $$$p$ , $$$y$ and $$$g$ known in advance. Function $$$y = g ^ {x} \ bmod p$ we consider unidirectional, that is, calculating a function with a known value of an argument is an easy task, and its inversion (finding an argument) with a known value of a function is difficult. (Inverse function $$$x = \ log_g y \ bmod p$ called the discrete logarithm function. There are currently no quick ways to calculate such a function for large simple $$$p$ .)



The exchange protocol consists of the following actions.

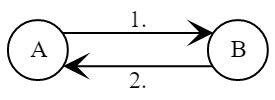
1. Alice picks a random $$$2 \ leq a \ leq p - 1$
   
   $$$Alice \ to \ left \ {A = g ^ a \ bmod p \ right \} \ to Bob$
2. Bob picks random $$$2 \ leq b \ leq p-1$
   
   Bob calculates a session key $$$K = A ^ b \ bmod p$
   
   $$$Bob \ to \ left \ {B = g ^ b \ bmod p \ right \} \ to Alice$
3. Alice calculates $$$K = B ^ a \ bmod p$
   
   

In this way, a shared secret session key is created $$$K$ . Due to the random selection of values $$$a$ and $$$b$ in a new session, a new session key will be received.



The protocol provides only the generation of new session keys (target G10). In the absence of a third trusted party, it does not provide authentication of the parties (target G1), due to the absence of passages with confirmation of ownership of the key, there is no authentication of the key (target G8). But, since the protocol does not use long “master” keys, we can say that it has the property of perfect direct secrecy (goal G9).



The protocol can only be used with communication channels into which an active cryptanalyst cannot intervene. Otherwise, the protocol becomes vulnerable to a simple “middle attack”.

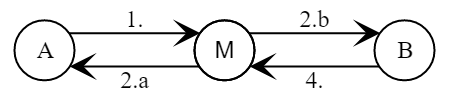
1. Alice picks a random $$$2 \ leq a \ leq p - 1$
   
   $$$Alice \ to \ left \ {A = g ^ a \ bmod p \ right \} \ to Mellory ~ (Bob)$
2. Mallory picks a random $$$2 \ leq m \ leq p-1$
   
   Mallory calculates a session key for a channel with Alice
   
   
   
   
   
   
   

   $$

   $$K_ {AM} = A ^ m \ bmod p = g ^ {am} \ bmod p$$
   
   
   
   
   
   
   $$$Mellory ~ (Alice) \ to \ left \ {M = g ^ m \ bmod p \ right \} \ to Bob$
   
   $$$Mellory ~ (Bob) \ to \ left \ {M = g ^ m \ bmod p \ right \} \ to Alice$
3. Alice calculates the session key for the channel with Mallory (thinking that Mallory is Bob)
   
   
   
   
   
   
   

   $$

   $$K_ {AM} = M ^ a \ bmod p = g ^ {am} \ bmod p$$
   
   
   
   
   
4. Bob picks random $$$2 \ leq b \ leq p-1$
   
   Bob calculates the session key for the channel with Mallory (thinking that Mallory is Alice)
   
   
   
   
   
   
   

   $$

   $$K_ {BM} = M ^ b \ bmod p = g ^ {bm} \ bmod p$$
   
   
   
   
   
   
   $$$Bob \ to \ left \ {B = g ^ b \ bmod p \ right \} \ to Mellory ~ (Alice)$
5. Mallory calculates a session key for a channel with Bob
   
   
   
   
   
   
   

   $$

   $$K_ {BM} = B ^ m \ bmod p = g ^ {bm} \ bmod p$$
   
   
   
   
   
   
   

As a result, Alice and Bob received new session keys, but they established a “secure” communication channel not with each other, but with an attacker who now has the ability to relay or change all transmitted messages between Alice and Bob.



The Diffie-Hellman protocol differs from most key distribution protocols due to the fact that it does not use other cryptographic primitives (encryption, digital signature or hashing functions), but in itself is in a sense a cryptographic primitive for constructing more complex protocols. It provides random number generation in a distributed system without a trusted center. Moreover, neither side can force the other side to use the old session key, unlike, for example, the Yahalom protocol.



The protocol can be changed so that instead of the multiplicative group of simple multiplication, use the additive group of addition of points of the elliptic curve. In this case, the parties will continue to choose some random integers, but do not raise the generator-number to a power, but multiply the generator-point by the desired number.

1. The parties agreed on a group of points of the elliptic curve $$$\ mathbb {E}$ its cyclic subgroup $$$\ mathbb {G}$ power $$$n = \ | \ mathbb {G} \ |$ and generator $$$G$ groups $$$\ mathbb {G}$ (or at least a sufficiently large subgroup of the group $$$\ mathbb {G}$ )
2. Alice picks a random $$$2 \ leq a \ leq n - 1$
   
   $$$Alice \ to \ left \ {A = a \ times G \ right \} \ to Bob$
3. Bob picks random $$$2 \ leq b \ leq n - 1$
   
   Bob calculates the point $$$K = b \ times A$
   
   $$$Bob \ to \ left \ {B = g \ times G \ right \} \ to Alice$
4. Alice calculates the point $$$K = a \ times B$

As a new session key, the parties can choose, for example, the first coordinate of the found point $$$K$ .

El Gamal Protocol

The El-Gamal protocol ( [ElGamal, 1984] , [ElGamal, 1985] ), due to the preliminary distribution of the public key of one of the parties, provides authentication of the key for this side. It can be guaranteed that only the owner of the corresponding private key can calculate the session key. However, confirmation of the receipt of the key (fulfillment of goals G1 and G8) is not part of the protocol.

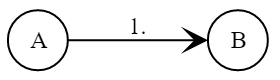
1. Alice and Bob choose common options $$$p$ and $$$g$ where $$$p$ Is a large prime, and $$$g$ - primitive field element $$$\ mathbb {Z} _p ^ *$ .
   
   Bob creates a pair of private and public keys $$$b$ and $$$K_B$ :
   
   
   
   
   
   
   

   $$

   $$\ begin {array} {l} b: 2 \ leq b \ leq p - 1, \\ K_B = g ^ b \ bmod p. \ end {array}$$
   
   
   
   
   
   
   Public key $$$K_B$ It is in the public open access for all parties. A cryptanalyst cannot replace him - the substitution will be noticeable.
2. Alice picks a secret $$$x$ and calculates the session key $$$K$
   
   
   
   
   
   
   

   $$

   $$K = K_B ^ {x} = g ^ {bx} \ bmod p.$$
   
   
   
   
   
   
   
   
   
   
   
   

   $$

   $$Alice \ to \ left \ {g ^ x \ bmod p \ right \} \ to Bob$$
   
   
   
   
   
3. Bob computes the session key
   
   
   
   
   
   
   

   $$

   $$K = (g ^ x) ^ {b} = g ^ {bx} \ bmod p.$$
   
   
   
   
   

The protocol does not guarantee the selection of a new session key in each protocol session (G10), and the use of a “master” key $$$K_B$ to transfer a session key allows an attacker to calculate all session keys from past sessions when a private key is compromised $$$b$ (goal G9).

MTI / A Protocol (0)

In 1986, C. Matsumoto ( Tsutomu Matsumoto ), I. Takashima ( Youichi Takashima ) and H. Imai ( Hideki Imai ) proposed several algorithms, later called the MTI protocol family ( [Matsumoto, Tsutomu, Imai 1986] ). Due to the preliminary distribution of the public keys of both parties, they provided implicit key authentication (target G7). That is, the session key was guaranteed to be received only by the owners of the corresponding public keys. We will consider one of the representatives of this family - the MTI / A protocol (0).



Previously, the parties agreed on the general parameters of the system. $$$p$ and $$$g$ where $$$p$ Is a large prime, and $$$g$ - primitive field element $$$\ mathbb {Z} _p ^ *$ .









Each of the parties (Alice and Bob) generated a pair of private and public keys:

$$

$$\ begin {array} {ll} Alice: & ~ a, ~~ K_A = g ^ a \ bmod p, \\ Bob: & ~ b, ~~ K_B = g ^ b \ bmod p. \\ \ end {array}$$

1. Alice generated a random number $$$R_A: ~ 2 \ leq R_A \ leq p-1$
   
   $$$Alice \ to \ left \ {g ^ {R_A} \ bmod p \ right \} \ to Bob$
2. Bob generated a random number $$$R_B: ~ 2 \ leq R_B \ leq p-1$
   
   Bob figured out a session key $$$K = (g ^ {R_A}) ^ b \ cdot K_A ^ {R_B} \ bmod p$
   
   $$$Bob \ to \ left \ {g ^ {R_B} \ bmod p \ right \} \ to Alice$
3. Alice computed the session key $$$K = (g ^ {R_B}) ^ a \ cdot K_B ^ {R_A} \ bmod p$

If the public keys $$$K_A$ and $$$K_B$ match your private keys $$$a$ and $$$b$ , then the session keys calculated by the participants match:

$$

$$\ begin {array} {lll} (g ^ {R_A}) ^ b \ cdot K_A ^ {R_B} \ bmod p & = & g ^ {b R_A + a R_B} \ bmod p, \\ (g ^ { R_B}) ^ a \ cdot K_B ^ {R_A} \ bmod p & = & g ^ {a R_B + b R_A} \ bmod p. \ end {array}$$

Due to the complexity of the discrete logarithm task, an attacker will not be able to obtain $$$a, R_A$ or $$$b, R_B$ from the transmitted messages, and the preliminary publication of public keys ensures that only legitimate users receive the session key. Random selection $$$R_A$ and $$$R_B$ ensures that both parties can be sure to create a new session key in each protocol session.



Like other representatives of cryptosystem protocols, MTI was not developed taking into account the possibility of compromising private master keys $$$a$ and $$$b$ (goal G9).

Station-to-Station Protocol

The STS protocol ( Station-to-Station , [Diffie, Oorschot, Wiener 1992] ) is intended for mobile communication systems. It uses the ideas of the Diffie-Hellman protocol and the RSA cryptosystem. A feature of the protocol is the use of an electronic signature mechanism for mutual authentication of the parties.



Previously, the parties agreed on the general parameters of the system. $$$p$ and $$$g$ where $$$p$ Is a large prime, and $$$g$ - primitive field element $$$\ mathbb {Z} _p ^ *$ .



Each side $$$A$ and $$$B$ possesses a long-term pair of keys: a private key for decrypting and creating an electronic signature $$$K _ {\ text {public}}$ and public key for encryption and signature verification $$$K _ {\ text {public}}$ .

$$

$$\ begin {array} {ll} A: K_ {A, \ text {private}}, K_ {A, \ text {public}}: \ forall M: & \ text {Verify} _A (M, S_A (M )) = true, \\ & D_A (E_A (M)) = M, \\ B: K_ {B, \ text {private}}, K_ {B, \ text {public}}: \ forall M: & \ text {Verify} _B (M, S_B (M)) = true, \\ & D_B (E_B (M)) = M. \\ \ end {array}$$

Where $$$\ text {Verify} _A (\ dots)$ it is a function of checking electronic signature on a public key $$$K_ {A, \ text {public}}$ , but $$$D_A$ - decryption function using the private key $$$K_ {A, \ text {private}}$ .



The protocol consists of four passes, three of which include the transmission of messages ( [Cheryomushkin 2009] ).

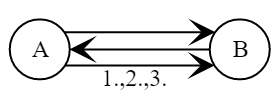
1. Alice picks a random number $$$R_A: 2 \ leq R_A \ leq p-1$ .
   
   $$$Alice \ to \ left \ {A, m_A = g ^ {R_A} \ bmod p \ right \} \ to Bob$
2. Bob picks a random number $$$R_B: 2 \ leq R_B \ leq p-1$ .
   
   Bob calculates a session key $$$K = m_A ^ {R_B} \ bmod p$ .
   
   $$$Bob \ to \ left \ {B, A, m_B = g ^ {R_B} \ bmod p, E_K (S_B (m_A, m_B)) \ right \} \ to Alice$
3. Alice calculates a session key $$$K = m_B ^ {R_A} \ bmod p$ .
   
   Alice verifies the signature in the message $$$E_K (S_B (m_A, m_B))$ .
   
   $$$Alice \ to \ left \ {A, B, E_K (S_A (m_A, m_B)) \ right \} \ to Bob$
4. Bob verifies the signature in the message $$$E_K (S_A (m_A, m_B))$ .

The protocol ensures the guarantee of the formation of new keys (G10), but not perfect direct secrecy (G9).



As the 1996 Lowe attack ( [Lowe 1996] ) showed, a protocol cannot guarantee authentication of subjects (target G1), keys (G7), and proof of ownership of the session key (G8). Although the attacker cannot gain access to the new session key if the protocol is used only to authenticate the subjects, Alice can mistake the attacker for Bob.

1. Alice picks a random number $$$R_A: 2 \ leq R_A \ leq p-1$ .
   
   $$$Alice \ to \ left \ {A, m_A = g ^ {R_A} \ bmod p \ right \} \ to Mellory ~ (Bob)$
   
   
2. $$$Mellory \ to \ left \ {M, m_A \ right \} \ to Bob$
   
   
3. Bob picks a random number $$$R_B: 2 \ leq R_B \ leq p-1$ .
   
   Bob calculates a session key $$$K = m_A ^ {R_B} \ bmod p$ .
   
   $$$Bob \ to \ left \ {B, M, m_B, E_K (S_B (m_A, m_B)) \ right \} \ to Mellory$
   
   
4. $$$Mellory ~ (Bob) \ to \ left \ {B, A, E_K (S_B (m_A, m_B)) \ right \} \ to Alice$
   
   
5. Alice calculates a session key $$$K = m_B ^ {R_A} \ bmod p$ .
   
   Alice verifies the signature in the message $$$E_K (S_B (m_A, m_B))$ .
   
   $$$Alice \ to \ left \ {A, B, E_K (S_A (m_A, m_B)) \ right \} \ to Mellory ~ (Bob)$
   
   

After successfully completing the protocol, Alice is confident that she is communicating with Bob.



Like all other “cryptosystem-protocols”, the Station-to-Station protocol is based on some external source of information about the public keys of participants, without questioning the correctness and reliability of this source. Which, in the general case, is wrong. If information about the keys of participants needs to be received externally at each protocol session (for example, if there are a lot of participants and there is no possibility to remember the keys for all), then the channel for obtaining public keys will be the main goal of an active cryptanalyst for the considered protocols. How to protect yourself from this using asymmetric cryptography primitives is in the next section.

Literature

• [Diffie, Hellman 1976] Diffie W., Hellman ME New directions in cryptography // Information Theory, IEEE Transactions on. - 1976. - Nov. - t. 22, No. 6. - p. 644-654. - ISSN 0018-9448. - DOI: 10.1109 / TIT.1976.1055638.
• [ElGamal, 1984] El Gamal T. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms // Proceedings of CRYPTO 84 on Advances in Cryptology. - Santa Barbara, California, USA: Springer-Verlag New York, Inc., 1985 .-- p. 10-18. - ISBN 0-387-15658-5. - URL: dl.acm.org/citation.cfm?id=19478.19480 .
• [ElGamal, 1985] El Gamal T. A public key cryptosystem and a signature scheme based on discrete logarithms // IEEE Transactions on Information Theory. - 1985. - July. - t. 31, No. 4. - p. 469-472. - DOI: 10.1109 / TIT.1985.1057074.
• [Matsumoto, Tsutomu, Imai 1986] Matsumoto T., Takashima Y., Imai H. On seeking smart publickey-distribution systems // Trans. Inst. Electron Commun. Eng. Jpn. Sect. E. T. 69. issue 2 .-- 02.1986. - from. 99-106.
• [Diffie, Oorschot, Wiener 1992] Diffie W., Van Oorschot PC, Wiener MJ Authentication
  
  and authenticated key exchanges // Designs, Codes and Cryptography. - 1992. - June. - t. 2, No. 2. - p. 107-125. - ISSN 1573-7586. - DOI: 10.1007 / BF00124891.
• [Lowe 1996] Lowe G. Some new attacks upon security protocols // CSFW '96 Proceedings of the 9th IEEE workshop on Computer Security Foundations. —Washington, DC, USA: IEEE Computer Society, 1996. - p. 162.
• [Cheremushkin 2009] Cheremushkin A. V. Cryptographic protocols: basic properties and vulnerabilities // Applied Discrete Mathematics. - 2009. - Nov. - issue. 2. - p. 115-150. - URL: cyberleninka.ru/article/n/kriptograficheskieprotokoly-osnovnye-svoystva-i-uyazvimosti.pdf .