Phoebe Wong, a Scientist and CFO at Equal Citizens, spoke about the cultural conflict in cognitive science. Elena Kuzmina translated the article into Russian.
A few years ago I watched a discussion about natural language processing. The “father of modern linguistics” Noam Chomsky and the New Guard spokesman Peter Norvig , director of research at Google, spoke. Chomsky pondered in which direction the sphere of natural language processing is moving, and said :
Suppose someone is going to liquidate the faculty of physics and wants to do it by the rules. According to the rules, this is to take an infinite number of videos about what is happening in the world, feed these gigabytes of data to the largest and fastest computer and conduct complex statistical analysis - well, you understand: Bayesian "back and forth" * - and you will get a certain forecast about what is about to happen outside your window. In fact, you will get a better forecast than the one given by the Faculty of Physics. Well, if success is determined by how close you are to the mass of chaotic raw data, then it’s better to do so than the way physicists do: no thought experiments on ideal surfaces, and so on. But you will not get the kind of understanding that science has always sought. What you get is just a rough idea of what is happening in reality.
* From Bayes probability - an interpretation of the concept of probability, in which, instead of the frequency or tendency to some phenomenon, probability is interpreted as a reasonable expectation, representing a quantitative assessment of a personal belief or state of knowledge. Artificial intelligence researchers use Bayesian statistics in machine learning to help computers recognize patterns and make decisions based on them.
Chomsky repeatedly emphasized this idea: today's success in processing natural language, namely the accuracy of forecasting, is not a science. According to him, throwing some huge piece of text into a “complex machine” is just to approximate raw data or collect insects, it will not lead to a real understanding of the language.
According to Chomsky, the main goal of science is to discover explanatory principles of how the system actually works, and the right approach to achieve this goal is to allow the theory to direct data. It is necessary to study the basic nature of the system by abstracting from “irrelevant inclusions” with the help of carefully designed experiments, that is, in the same way as was accepted in science from the time of Galileo.
In his words:
A simple attempt to deal with raw chaotic data is unlikely to lead you anywhere, just as Galileo would not lead anywhere.
Subsequently, Norwig responded to Chomsky’s claims in a long essay . Norvig notes that in almost all areas of the application of language processing: search engines, speech recognition, machine translation and answering questions, trained probabilistic models prevail because they work much better than old tools based on theoretical or logical rules. He says that Chomsky’s criterion of success in science - the emphasis on the question “why” and the understatement of the importance of “how” - is wrong.
Confirming his position, he quotes Richard Feynman: "Physics can develop without evidence, but we cannot develop without facts." Norwig recalls that probabilistic models generate several trillion dollars a year, while descendants of Chomsky’s theory earn far less than a billion, citing Chomsky’s books sold on Amazon.
Norwig suggests that Chomsky’s contempt for “Bayesian back and forth” is due to the split between the two cultures in the statistical modeling described by Leo Breiman:
- A data modeling culture that assumes nature is a black box where variables are connected stochastically. The work of modeling experts is to determine the model that best fits the associations that underlie it.
- The culture of algorithmic modeling implies that associations in a black box are too complex to be described using a simple model. The work of model developers is to select the algorithm that best evaluates the result using input variables, without expecting that the true basic associations of variables inside the black box can be understood.
Norvig suggests that Chomsky is not so much polemicizing with probabilistic models as such, but rather does not accept algorithmic models with “quadrillion parameters”: they are not easy to interpret and therefore they are useless for solving the “why” questions.
Norwig and Breiman belong to another camp - they believe that systems such as languages are too complex, random, and arbitrary to be represented by a small set of parameters. And abstracting from difficulties is akin to making a mystical tool tuned to a certain permanent area that does not actually exist, and therefore the question of what language is and how it works is overlooked.
Norwig reaffirms his thesis in another article , where he argues that we should stop acting like our goal is to create extremely elegant theories. Instead, you need to accept complexity and use our best ally - unreasonable data efficiency. He points out that in speech recognition, machine translation, and almost all machine learning applications for web data, simple models like n-gram models or linear classifiers based on millions of specific functions work better than complex models. who are trying to discover the general rules.
What attracts me most in this discussion is not what Chomsky and Norvig disagree with, but what they are united in. They agree that analyzing huge amounts of data using statistical learning methods without understanding variables provides better predictions than a theoretical approach that tries to model how variables are related to each other.
And I'm not the only one who is puzzled by this: many people with a mathematical background with whom I spoke also find this contradictory. Shouldn't the approach that is best suited for modeling basic structural relationships also have the greatest predictive power? Or how can we accurately predict something without knowing how everything works?
Predictions Against Causation
Even in academic fields, such as economics and other social sciences, the concepts of predictive and explanatory power are often combined with each other.
Models that demonstrate a high ability to explain are often considered highly predictive. But the approach to building the best predictive model is completely different from the approach to building the best explanatory model, and modeling decisions often lead to compromises between the two goals. Methodological differences are illustrated in Introduction to Statistical Learning (ISL).
Predictive modeling
The fundamental principle of predictive models is relatively simple: evaluate Y using a set of readily available input data X. If the error X is on average zero, Y can be predicted using:
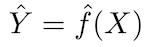
where ƒ is the systematic information about Y provided by X, which leads to Ŷ (prediction of Y) for a given X. The exact functional form is usually not significant if it predicts Y, and ƒ is considered a “black box”.
The accuracy of this type of model can be decomposed into two parts: a reducible error and a fatal error:
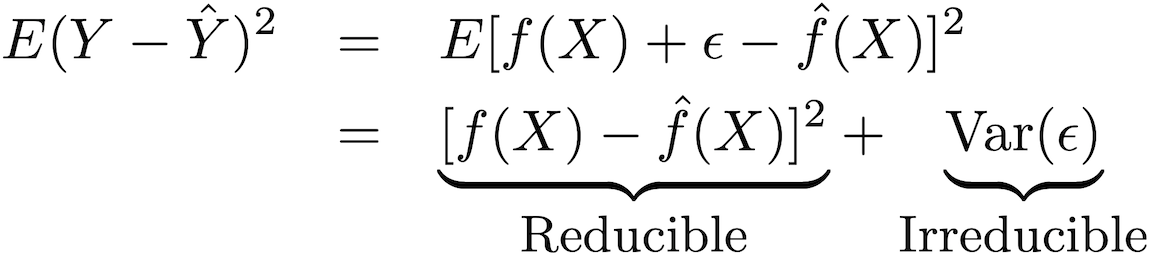
In order to increase the accuracy of forecasting the model, it is necessary to minimize the reducible error, using the most suitable methods of statistical training for estimation in order to evaluate
Output modeling
ƒ cannot be regarded as a “black box” if the goal is to understand the relationship between X and Y (how Y changes as a function of X). Because we cannot determine the effect of X on Y without knowing the functional form ƒ.
Almost always, when modeling conclusions, parametric methods are used to estimate ƒ. The parametric criterion refers to how this approach simplifies the estimation of ƒ by taking the parametric form ƒ and evaluating ƒ through the proposed parameters. There are two main steps in this approach:
1. Make an assumption about the functional form ƒ. The most common assumption is that ƒ is linear in X:
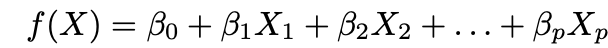
2. Use the data to fit the model, that is, find the values of the parameters β₀, β₁, ..., βp such that:
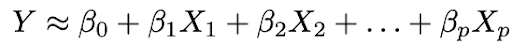
The most common model fitting approach is the Least Squares (OLS) method.
The tradeoff between flexibility and interpretability
You may already be wondering: how do we know that ƒ is linear? In fact, we will not know, since the true form ƒ is unknown. And if the selected model is too far from the real ƒ, then our estimates will be biased. So why do we want to make such an assumption in the first place? Because there is an inherent compromise between model flexibility and interpretability.
Flexibility refers to the range of forms that a model can create to fit the many different possible functional forms ƒ. Therefore, the more flexible the model, the better fit it can create, which increases the accuracy of forecasting. But a more flexible model is more complex and requires more parameters to fit, and estimates often become too complex for the associations of any individual predictors and prognostic factors to be interpreted.
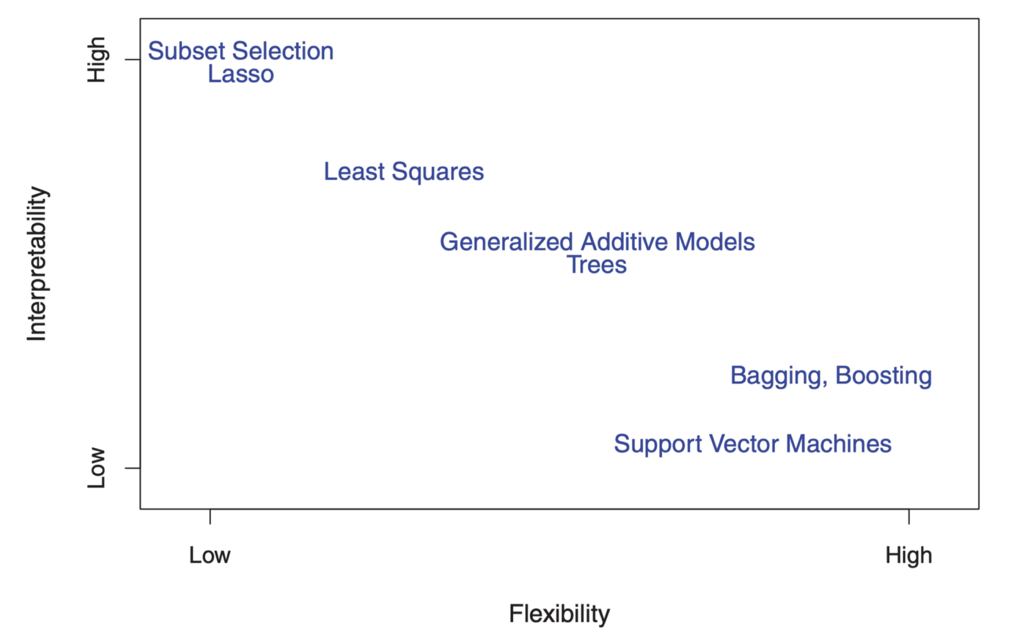
On the other hand, the parameters in the linear model are relatively simple and interpretable, even if it does not perform an accurate forecast very well. Here is a great diagram in ISL that illustrates this trade-off in various statistical training models:
"
 "
"
As you can see, more flexible machine learning models with better forecasting accuracy, such as the support vector method and enhancement methods, at the same time have low interpretability. Inference modeling also refuses the forecasting accuracy of the interpreted model, making a confident assumption about the functional form f.
Causal Identification and Counterfactual Reasoning
But wait a moment! Even if you use a well-interpreted model with good fit, you still cannot use these statistics as a separate evidence of causality. This is because of the old, weary cliche "correlation is not causation."
Here is a good example : suppose you have data on the length of a hundred flagpoles, the length of their shadows and the position of the sun. You know that the shadow length is determined by the pole length and the position of the Sun, but even if you set the pole length as a dependent variable and the shadow length as an independent variable, your model will still fit statistically significant coefficients and so on.
That is why causal relationships cannot be made only by statistical models and require basic knowledge - the alleged causality should be justified by some preliminary theoretical understanding of the relationship. Therefore, data analysis and statistical modeling of cause-effect relationships are often largely based on theoretical models.
And even if you have good theoretical justification for saying that X causes Y, identifying a causal effect is still often very difficult. This is because evaluating a causal relationship involves identifying what would happen in a counter-active world in which X did not take place, which by definition is not observable.
Here is another good example : suppose you want to determine the health effects of vitamin C. Do you have data on whether someone is taking vitamins (X = 1 if he is taking; 0 - not taking), and some binary health outcomes (Y = 1 if they are healthy; 0 - not healthy) that looks like that:
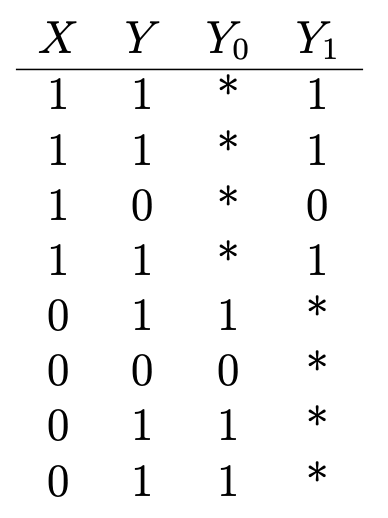
Y₁ is the health outcome of those who take vitamin C, and Y₀ is the health outcome of those who are not. To determine the effect of vitamin C on health, we evaluate the average treatment effect:
But in order to do this, it is important to know what the health consequences of those who take vitamin C would be if they did not take any vitamin C, and vice versa (or E (Y₀ | X = 1) and E (Y₁ | X = 0)), which are indicated by asterisks in the table and represent unobserved counterfactual results. The average treatment effect cannot be evaluated sequentially without this input.
Now imagine that already healthy people, as a rule, try to take vitamin C, while already unhealthy people do not. In this scenario, evaluations would show a strong healing effect, even if vitamin C did not actually affect health at all. Here, the previous state of health is called a mixed factor, which affects both vitamin C intake and health (X and Y), which leads to distorted estimates. The safest way to get a consistent estimate of θ is to randomize treatment through an experiment so that X is not dependent on Y.
When treatment is prescribed randomly, the result of the group not receiving the drug, on average, becomes an objective indicator for the counterfactual results of the group receiving the treatment, and ensures that there is no distorting factor. A / B testing is guided by this understanding.
But randomized experiments are not always possible (or ethical, if we want to study the health effects of smoking or eating too many chocolate chip cookies), and in these cases, the causal effects should be estimated from observations with often non-randomized treatment.
There are many statistical methods that identify causal effects in non-experimental conditions. They do this by constructing counterfactual results or modeling random prescriptions of treatment in observational data.
It is easy to imagine that the results of these types of analysis are often not very reliable or reproducible. And even more important: these levels of methodological obstacles are not intended to improve the accuracy of model prediction, but to present evidence of causality through a combination of logical and statistical conclusions.
It is much easier to measure the success of a prognostic than a causal model. Although there are standard performance indicators for prognostic models, it is much more difficult to assess the relative success of causal models. But if it’s difficult to trace cause-effect relationships, this does not mean that we must stop trying.
The main point here is that prognostic and cause-effect models serve completely different purposes and require completely different data and statistical modeling processes, and often we have to do both.
An example from the film industry illustrates: studios use forecasting models to forecast box office grossing, to predict the financial results of film distribution, to assess the financial risks and profitability of their portfolio of films, etc. But forecasting models will not bring us closer to understanding the structure and dynamics of the movie market and will not help in making investment decisions, because at the earlier stages of the film production process (usually years before the release date), when investment decisions are made, the variance of possible The results are high.
Therefore, the accuracy of forecast models based on initial data in the early stages is greatly reduced. Predictive models are getting closer to the start date of film distribution, when most production decisions have already been made and the forecast is no longer particularly feasible and relevant. On the other hand, the modeling of cause-and-effect relationships allows studios to find out how various production characteristics can influence potential income in the early stages of film production and are therefore crucial to informing about their production strategies.
Increased focus on predictions: was Chomsky right?
It is not difficult to understand why Chomsky is upset: prognostic models dominate in the scientific community and in industry. A textual analysis of academic preprints shows that the fastest growing areas of quantitative research are paying more and more attention to forecasts. For example, the number of articles in the field of artificial intelligence that mention “prediction” has more than doubled, while articles on findings have halved since 2013.
Data science education programs largely ignore cause-and-effect relationships. And data science in business mainly focuses on predictive models. Prestigious industry competitions such as the Kaggle and Netflix prize are based on improving predictive performance indicators.
On the other hand, there are still many areas in which insufficient attention is paid to empirical forecasting, and they can benefit from the achievements obtained in the field of machine learning and predictive modeling. But to present the current state of affairs as a cultural war between the “Chomsky Team” and the “Norvig Team” is incorrect: there is no reason why it is necessary to choose only one option, because there are many opportunities for mutual enrichment between the two cultures. Much work has been done to make machine learning models more understandable. For example, Susan Ati from Stanford uses machine learning methods in a causal relationship methodology.
To finish on a positive note, recall the works of Jude Perle . Pearl led a research project on artificial intelligence in the 1980s, which allowed machines to reason probabilistically using Bayesian networks. However, since then he has become the biggest critic of how the attention of artificial intelligence exclusively to probabilistic associations and correlations became an obstacle to achievements.
Sharing Chomsky’s opinion, Pearl argues that all the impressive accomplishments of deep learning come down to fitting the curve to the data. Today, artificial intelligence is stuck doing the same things (for predicting and diagnosing and classifying) that machines could do 30 years ago. Now cars are only marginally better, with prediction and diagnostics being “only the tip of human intelligence.”
He believes that the key to creating truly intelligent machines that think like people is teaching machines to think about cause and effect, so these machines can ask conflicting questions, plan experiments, and find new answers to scientific questions.
His work over the past three decades has focused on creating a formal language for machines to make causality possible, similar to his work on Bayesian networks that allowed machines to create probabilistic associations. In one of his articles, he states:
Most of human knowledge is organized around causal rather than probabilistic relationships, and the grammar of calculating probability is not enough to understand these relationships ... It is for this reason that I consider myself only half Bayesian.
It seems that data science will only benefit if we have more nibbles.