Inside The JeMalloc. Core Data Structures: Pairing Heap & Bitmap Tree

The topic of Allocators often pops up on the Internet: indeed, an allocator is a kind of cornerstone, the heart of any application. In this series of posts I want to talk in detail about one very entertaining and eminent allocator - JeMalloc , supported and developed by Facebook and used, for example, in bionic [Android] lib C.



On the network, I could not find any details that fully reveal the soul of this allocator, which ultimately affected the impossibility of making any conclusions about the applicability of JeMalloc in solving a particular problem. There was a lot of material and, in order to read it was not tiring, I suggest starting with the basics: The Basic Data Structures used in JeMalloc.



Under the cat, I’m talking about Pairing Heap and Bitmap Tree , which form the foundation of JeMalloc. At this stage, I do not touch on the topic of multithreading and Fine Grained Locking , however, continuing the series of posts, I will definitely tell you about these things, for the sake of which, in fact, various kinds of Exotics are created, in particular the one described below.



Bitmap_s is a tree-like data structure that allows you to:

• Quickly find the first set / unset bit in a given bit sequence.
• Change and get the value of a bit with index i in a given sequence of bits.
• The tree is built according to a sequence of n bits and has the following properties:
• The base unit of the tree is the node, and the base unit of the node is the bit. Each node consists of exactly k bits. The bitness of a node is selected so that the logical operations on a selected range of bits are calculated as quickly and efficiently as possible on a given computer. In JeMalloc, a node is represented by an unsigned long type.
• The height of the tree is measured in levels and for a sequence of n bits is H = $$$\ log_ {k} {n} log k (n)$ levels.
• Each level of the tree is represented by a sequence of $$$countOfNodesOnLevel = integerCeil (\ frac {n} {{k} ^ {H - currentLevel + 1}})$ nodes, which is equivalent to a sequence of $$$countOfBitsOnLevel = countOfNodesOnLevel * k$ bit.
• The highest (root) level of the tree consists of k bits, and the lowest - of n bits.
• Each bit of a node of level L determines the state of all bits of a child node of level L - 1: if the bit is set to busy, then all bits of the child node are also set to busy, otherwise, bits of the child node may have 'busy' and 'free' state.

It is reasonable to represent bitmap_t in two arrays: the first, the dimension equal to the number of all tree nodes — to store the tree nodes, the second, the tree height dimension — to store the offset of the beginning of each level in the array of tree nodes. With this method of specifying a tree, the root element can go first, and then, in sequence, the nodes of each of the levels. However, JeMalloc authors store the root element last in the array, and in front of it are the nodes of the underlying tree levels.



As an illustrative example, take a sequence of 92 bits and K = 32 mind. We assume that the state is 'free' - denoted by a single bit, and the state 'busy' - zero. Assume also that in the original bit sequence, the bit with index 1 (counting from zero, from right to left in the figure) is set to the busy state. Then bitmap_t for such a bit sequence will look like the image below:







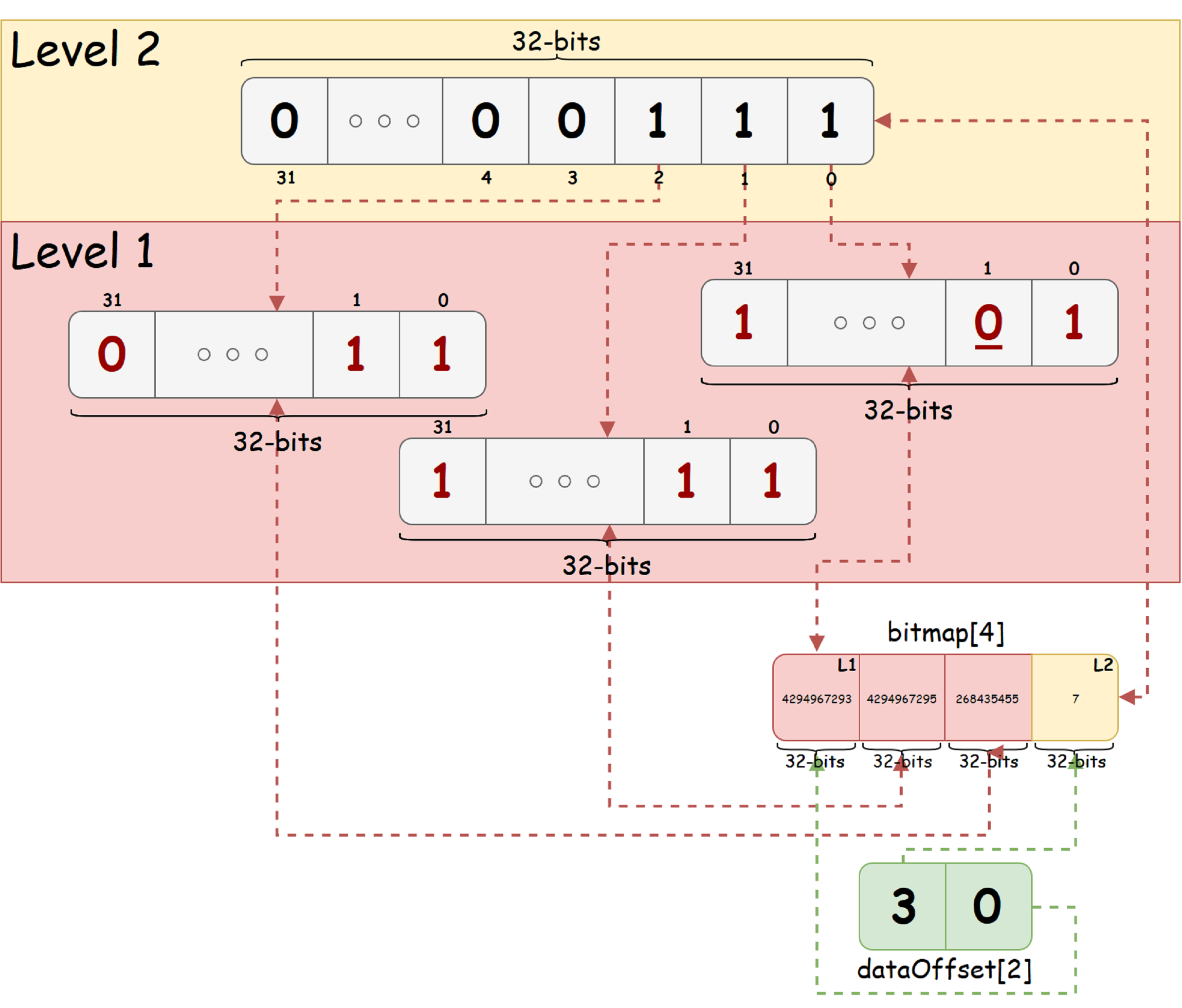
From the figure we see that the resulting tree has only two levels. The root level contains 3 unit bits, which indicates the presence of both free and occupied bits in each of the child nodes of the corresponding bit. In the lower right corner, you can see the Tree view in two arrays: all tree nodes and offsets of each level in the node array.



Assuming that bitmap_t is represented by two arrays (a data array and an array of tree level offsets in the data array), we describe the operation of searching for the first least significant bit in a given bitmap_t:

• Starting from the root node, we perform the search operation for the first least significant bit of the node: to solve this problem, modern processors provide special instructions that can significantly reduce the search time. We will save the found result in the FirstSetedBit variable.
• At each iteration of the algorithm, we will support the sum of the positions of the found bits: countOfSettedBits + = FirstSetedBit
• Using the result of the previous step, we go to the child node of the first least significant unit bit of the node and repeat the previous step. The transition is carried out according to the following simple formula: $$$currentNode = bitmapData [levelOffsetArray [currentLevel] + sumOfBits]$
• The process continues until the lowest level of the tree is reached. countOfSettedBits - number of the desired bit in the input bit sequence.

Pairing Heap is a heap-like tree data structure that allows:

• Insert an element with constant time complexity - O (1) and amortized cost O (log N) or O (1) - depending on the implementation.
• Search at least for constant time - O (1)
• Merge two Pairing Heap with constant time complexity - O (1) and amortized cost O (log N) or O (1) - depending on implementation
• Delete an arbitrary element (in particular, a minimal one) with a temporary complexity estimate in O (N) and amortized complexity estimate in O (log N)

More formally speaking, Pairing Heap is an arbitrary tree with a dedicated root that satisfies the properties of the heap (the key of each vertex is no less / no more than the key of its parent).

A typical Pairing Heap in which the value of the child node is less than the value of the parent node (aka Min Pairing Heap) looks something like this:







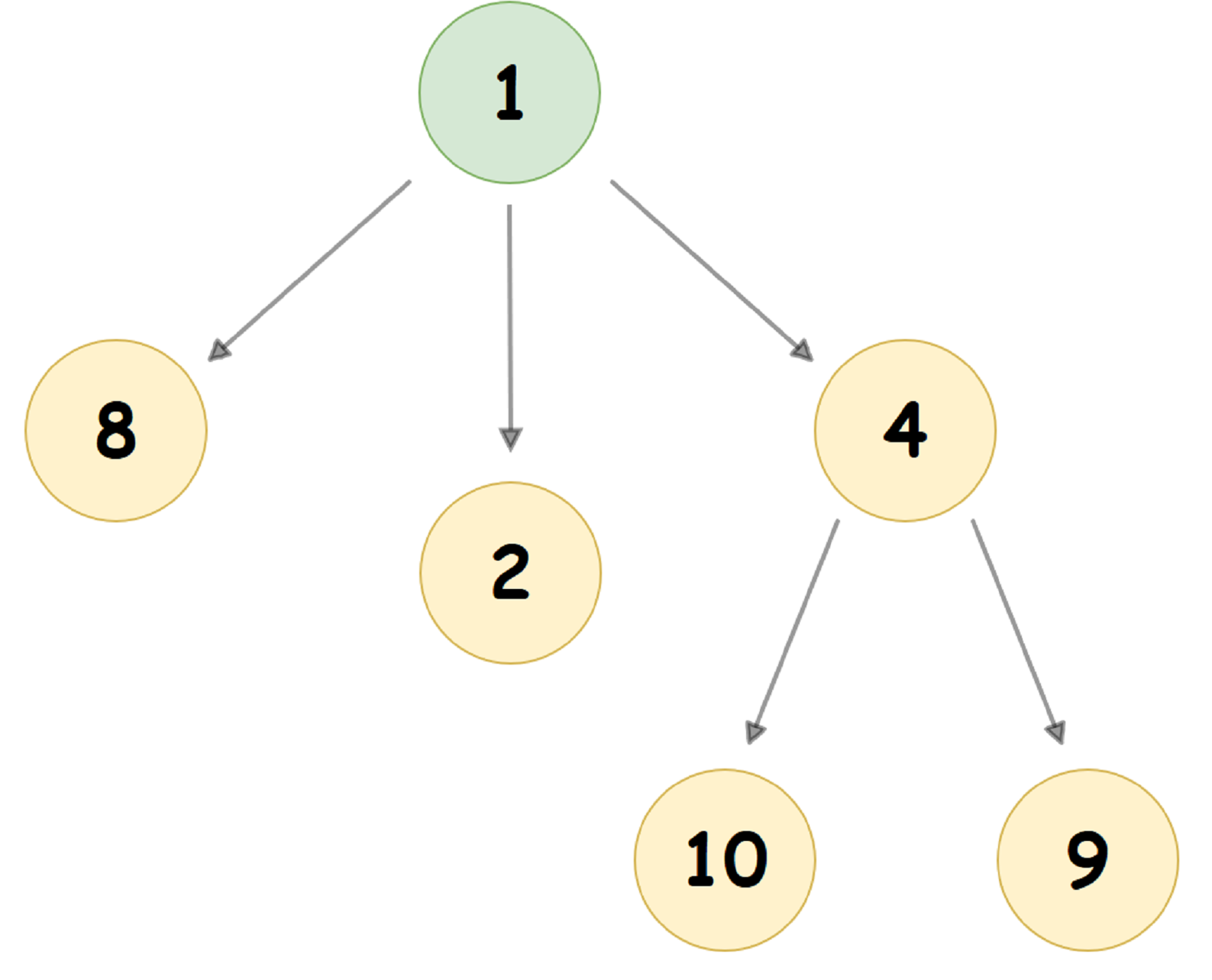
As a rule, Pairing-Heap is represented in the computer’s memory in a completely different way: each node of the Tree stores 3 pointers:

• Pointer to the leftmost child node of the current node
• Pointer to the node's left brother
• Pointer to the right sibling of the node

If any of the indicated nodes is missing, the corresponding node pointer is nullified.

For the heap presented in the figure above, we get the following representation:







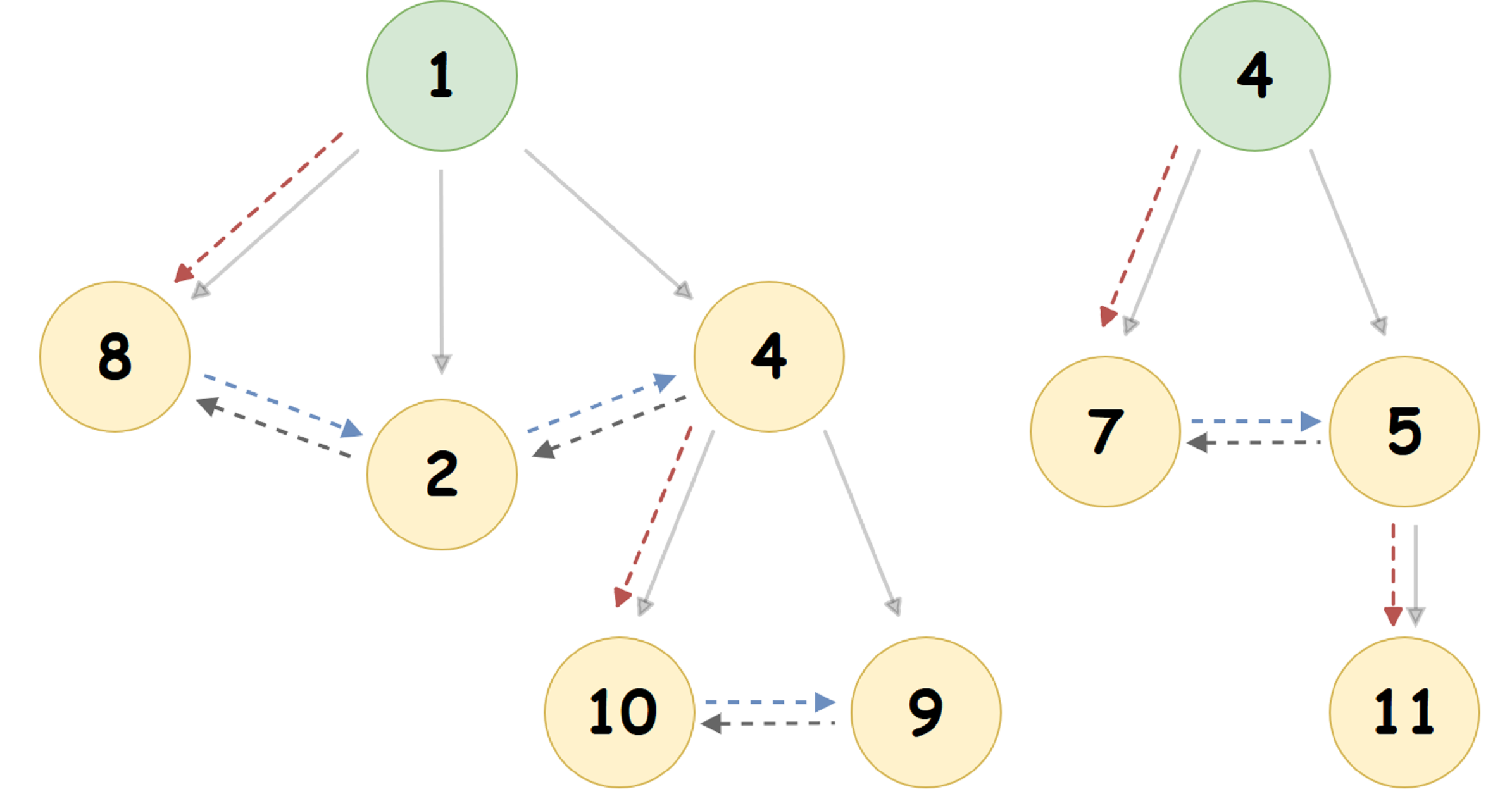
Here, the pointer to the leftmost child node is indicated by a red dotted arrow, the pointer to the right brother of the node is blue, and the pointer to the left brother is gray. The solid arrow shows the Pairing Heap representation in a tree-like form that is common for humans.



Please note the following two facts:

• At the root of the heap there are always no right and left brothers.
• If any node U has a non-zero pointer to the left-most child node, then this node will be the 'Head' of the doubly linked list of all the child nodes of U. This list is called siblingList.

Next, we list the algorithm of the main operations in the Min Pairing-Heap :

• Insert node into Pairing Heap:
  
  
  
  Let there be given a Pairing Heap with a root and a value in it {R, V_1} , as well as a node {U, V_2} . Then, when inserting a U node into a given Pairing Heap:
  
  
  • If the condition V_2 <V_1 is satisfied: U becomes the new root node of the heap, 'crowding out' the root R to the position of its left child node. At the same time, the right brother of the node R becomes its oldest left-most node, and the pointer to the left-most node of the node R becomes zero.
  • Otherwise: U becomes the leftmost child node of the root R, and its old brother becomes the oldest leftmost node of the root R.
• Merging Two Pairing Heap:
  
  
  
  Let two Pairing Heaps with roots and values ​​in them {R_1, V_1} , {R_2, V_2}, respectively, be given. We describe one of the algorithms for merging such heaps into the resulting Pairing Heap:
  
  
  • Choose the heap with the lowest value in the root. Let it be a bunch of {R_1, V_1}.
  • 'Detach' the root R_1 from the selected heap: for this, we simply null its pointer to the left-most child node.
  • With the new pointer to the leftmost child node of the root R_1, make the root R_2. Note that from now on, R_2 loses root status and is a normal node in the resulting heap.
  • We set the right brother of the node R_2: with the new value, make the old (before zeroing) pointer to the leftmost child node of the root R_1, and for R_1, respectively, update the pointer to the left brother.

Consider the merge algorithm using a specific example:







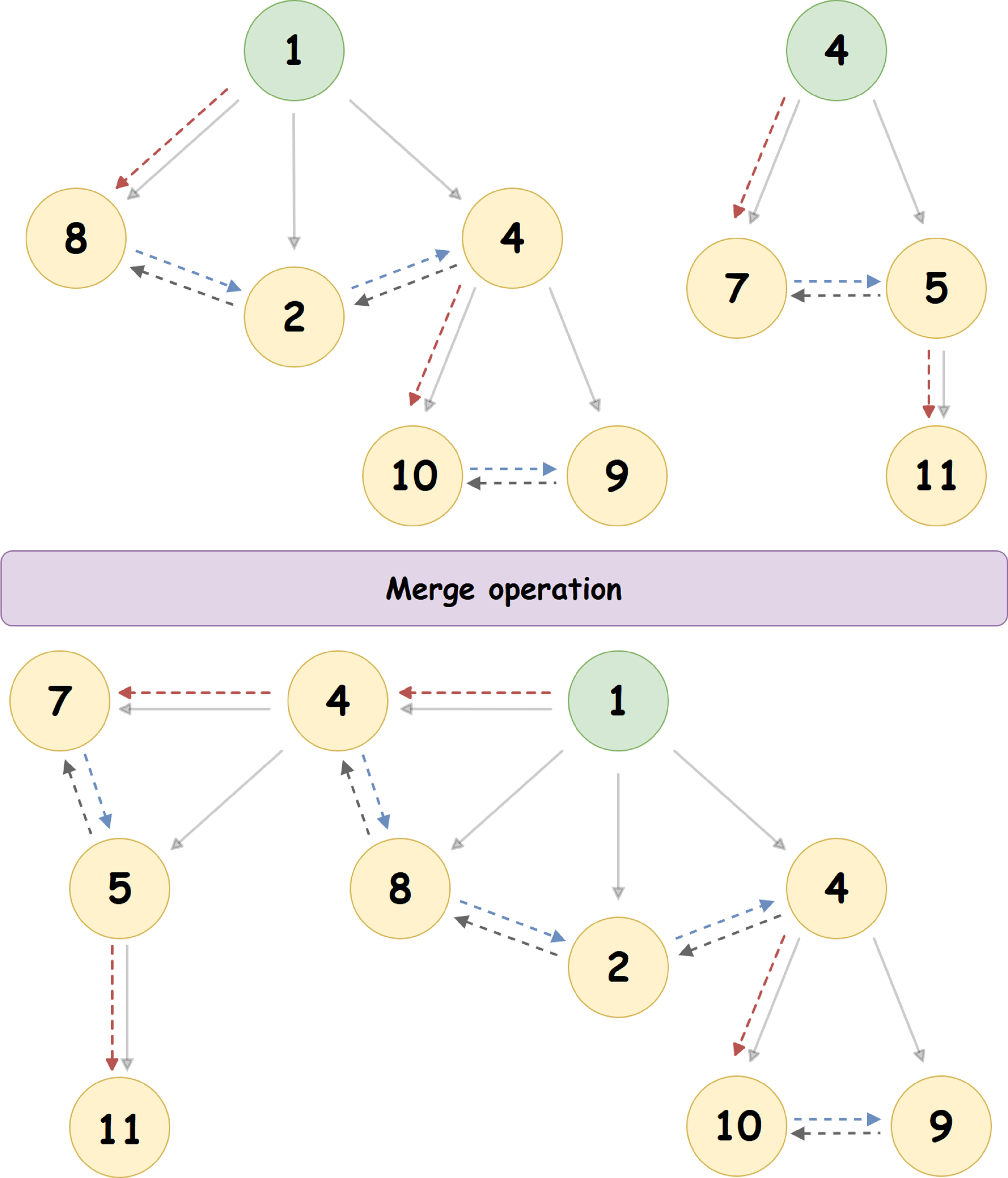
Here, the heap with the root '4' joins the heap with the root '1' (1 <4), becoming its left-most child node. The pointer to the right brother of the node '4' - is updated, as well as the pointer to the left brother of the node '8'.

• Removing the root (node ​​with the minimum value) Pairing Heap:
  
  
  
  There are several algorithms for removing a node from the Pairing Heap, guaranteed to give an amortized complexity estimate in O (log N). We describe one of them, called the multipass algorithm and used in JeMalloc:
  
  
  
  
  • We delete the root of the given heap, leaving only its leftmost child node.
  • The leftmost child node forms a doubly linked list of all the child nodes of the parent node, and in our case, the previously deleted root. We will sequentially go through this list to the end and, considering the nodes as the roots of independent Pairing Heap, perform the operation of merging the current element of the list with the next, placing the result in a pre-prepared FIFO queue.
  • Now that the FIFO queue is initialized, we will iterate over it, performing the operation of merging the current element of the queue with the next. The result of the merger is placed at the end of the queue.
  • We repeat the previous step until one element remains in the queue: the resulting Pairing Heap.

A good example of the process described above:

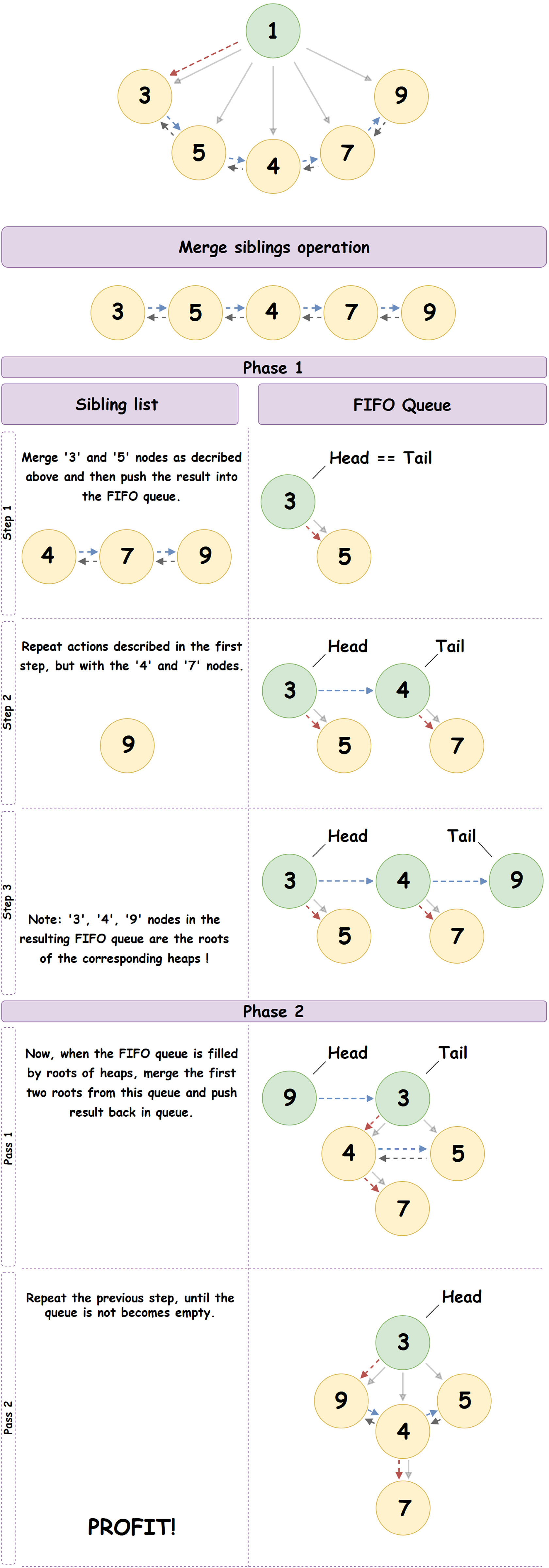
• Removing an arbitrary non-root node Pairing Heap:
  
  
  
  Consider the deleted node as the root of some subtree of the original Heap. First, delete the root of this subtree, following the previously described algorithm for removing the Pairing Heap root, and then, perform the procedure of merging the resulting tree with the original one.
• Getting the minimum Pairing Heap element:
  
  
  
  Just return the value of the heap root.

However, our acquaintance with Pairing Heap does not end there: Pairing Heap allows you to perform some operations not immediately, but only when the need arises for them. In other words, Pairing Heap allows you to perform operations 'Lazily' , thereby lowering the amortized cost of some of them.

Suppose we made K insertions and K deletes in Pairing Heap. Obviously, the result of these operations becomes necessary only when we request the minimum element from the heap.

Let's consider how the algorithm of actions of the previously described operations will change during their Lazy implementation:



Taking advantage of the fact that the Kuchi root has at least two null pointers, we will use one of them to represent the head of a doubly linked list (hereinafter auxList ) of elements inserted into the heap, each of which will be considered as the root of an independent Pairing Heap. Then:

• Lazy node insertion in Pairing Heap:
  
  
  
  When inserting the specified U node into the Pairing Heap { R_1 , V_1 }, we put it in auxList - after the head of the list:

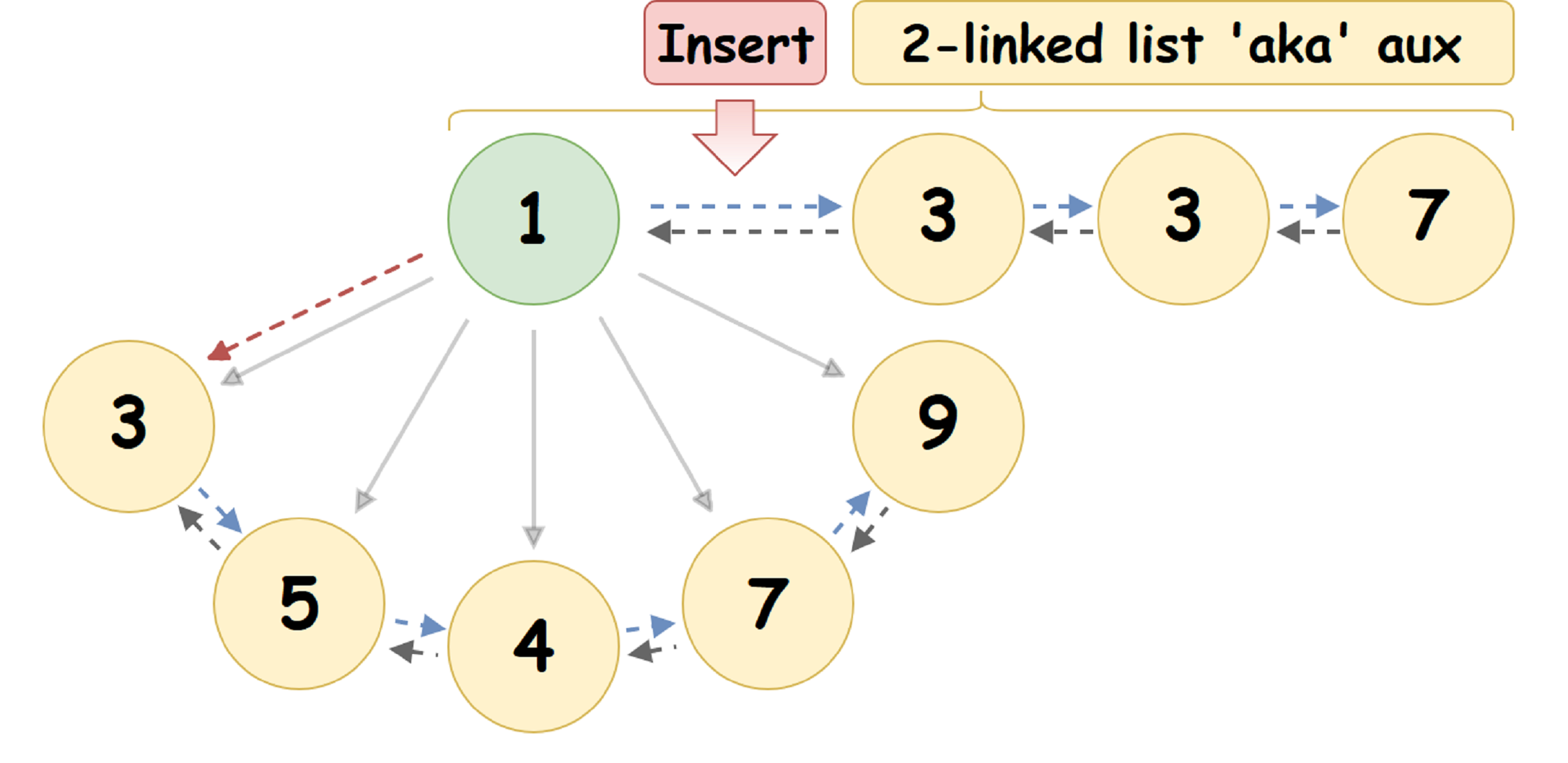
• The lazy merging of two Pairing Heap:
  
  
  
  Lazy Merging two Pairing Heap, similar to the Lazy node insertion, where the inserted node is the root (head of the doubly connected auxList) of one of the heaps.
• Lazy getting the minimum Pairing Heap element:
  
  
  
  When requesting a minimum, we go through auxList to the list of roots of independent Pairing Heap, pairwise combining the elements of this list with the merge operation, and return the value of the root containing the minimum element to one of the resulting Pairing Heap.
• Lazy removal of the minimum Pairing Heap element:
  
  
  
  When requesting the removal of the minimum element specified by the Pairing Heap, first we find the node containing the minimum element, and then remove it from the tree in which it is the root, inserting its subtrees into the auxList of the main heap.
• Lazy removal of an arbitrary non-root Pairing Heap node:
  
  
  
  When deleting an arbitrary non-root Pairing Heap node, the node is removed from the heap, and its child nodes are inserted into the auxList of the main Heap.

Actually, the use of the Lazy Pairing Heap implementation reduces the amortized cost of insertion and removal of arbitrary nodes in the Pairing Heap: from O (log N) to O (1).



That's all, and below you will find a list of useful links and resources:



[0] JeMalloc Github Page

[1] Original article on Pairing Heaps

[2] Original article on Lazy Implementation Pairing Heaps

[3] Telegram channel about code optimizations, C ++, Asm, 'low level' and nothing more than that!



To be continued…