How the Levenberg-Marquardt Method Works
The Levenberg-Marquardt algorithm is simple. The Levenberg-Marquardt algorithm is efficient.
And they say about him that he is somewhere in between the gradient descent and the Newton method, whatever that means. Well, it’s sort of sorted out with Newton’s method and its connection with gradient descent. But what do they mean when they utter this profound phrase? Let's try a little sneak.
In his articles, Comrade Levenberg [K. A Method for the Solution of Certain Problems in Last Squares. Quart. Appl. Math. 1944. Vol. 2. P. 164-168.], And after him citizen Marquardt [Marquardt, Donald (1963). "An Algorithm for Least-Squares Estimation of Nonlinear Parameters." SIAM Journal on Applied Mathematics. 11 (2): 431–441.] Considered the least squares problem, which looks like this:
,
which can be written easier in vector form
.
And you can even easier by completely scoring on the least squares. This will not affect the story.
So, the problem is considered
.
Such a problem arises so often that the importance of finding an effective method for solving it can hardly be overestimated. But we will start from another. In a previous article, it was shown that the well-known gradient descent method, and not only it, can be obtained from the following considerations. Let's say we come to some point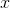
in which the minimized function matters 
. We define an auxiliary function at this point 
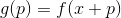, as well as some of its model 
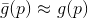. For this model, we pose an auxiliary problem
Where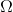
- a certain predetermined set of permissible values, chosen so that the problem has a simple solution and the function 
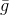approximated quite accurately 
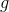on 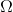. This scheme is called the trust region method, and many 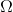on which the value of the model function is minimized - the confidence region of this function. For gradient descent, we took 
, for Newton's method 
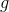, and as a model for the linear part of the Taylor expansion 
.
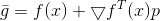Let's see what happens if we complicate the model by taking
.
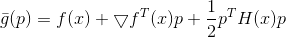We minimize this model function on an elliptic confidence region
(multiplier added for ease of calculation). Applying the Lagrange multiplier method, we obtain the problem
,
whose solution satisfies the equality
or
Here, in contrast to what we saw earlier when using the linear model, the direction p is not only dependent on the metric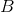
, but also on the choice of the size of the trust region 
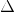, which means the linear search technique is not applicable (at least reasonably). It also turns out to be difficult to explicitly determine 
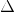corresponding to . However, it is quite obvious that with increasing length 
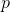will decrease. If in doing so we still impose the condition 
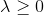, then the step length will be no more than that which Newton's method would give (all-fashionable, without modifications and conditions).
So we can instead for a given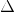 look for the right value , do exactly the opposite: find this 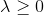under which the condition 
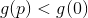. This is a kind of replacement for the late search in this case. Marquardt proposed the following simple procedure:
Here
and 
- constants that are method parameters. Multiplication by 
corresponds to the expansion of the confidence region, and multiplication by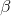 
- its narrowing.
The specified technique can be applied to any objective function. Note that here the positive definiteness of the Hessian is no longer required, in contrast to the case considered earlier, when the Newton method was presented as a special case of the sequential descent method. Not even its non-degeneracy is required, which in some cases is very important. However, in this case, the price of the direction search increases, since each change leads to the need to solve a linear system to determine .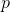
Let's see what happens if we apply this approach to the least squares problem.
Gradient Function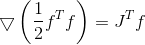
her hessian 
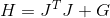where 
. We substitute and get the following system that determines the direction of the search
.
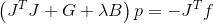It is quite acceptable, but calculating the second derivatives of a vector function can be quite expensive. Marquardt proposed to use the function itself to bypass this problem.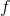
, and its linear approximation 
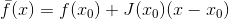at which the matrix 
turns to zero. If now as 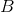take the identity matrix 
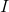, then we obtain the standard form of the Levenberg-Marquardt method for solving the least squares problem:
.
For this method of determining the direction of descent, Marquardt proved the theorem that with aspiration to infinity direction 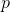tends to anti-gradient. An interested reader can find a rigorous proof in the base article, but I hope that this statement itself has become quite obvious from the logic of the method. To some extent, it justifies the ubiquitous reference to the fact that with an increase in lambda (which for some reason I often call the regularization parameter) we get a gradient descent. Actually, nothing of the kind - we would get it only in the limit, in the very one where the step length tends to zero. It is much more important that for a sufficiently large lambda value, the direction that we get will be the direction of descent , which means we get the global convergence of the method . And here is the second part of the statement that when the lambda tends to zero we get the Newton method, it is clearly true, but only if we accept instead 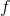its linear approximation 
.
It would seem that all. We minimize the norm of the vector function in the elliptic metric - we use the Levenberg-Marquardt. We are dealing with a function of a general form and have the ability to calculate the matrix of second derivatives - for Wells, use the general confidence method of the region. But there are perverts ...
Sometimes the Levenberg-Marquardt method to minimize function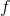 they call an expression like this:
.
Everything seems to be the same, but here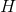
- second matrix! derivative functions 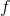. Formally, this has a right to exist, but it is a perversion. And that's why. The same Marquardt in his article proposed a method for solving a system of equations 
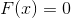by minimizing the function 
the described method. If as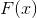 
take the gradient of the objective function, then we really get the reduced expression. And the perversion is because
the minimization problem generated by the system of nonlinear equations generated by the minimization problem is solved .
Double strike. Such an expression, at least, is not better than the first equation of a spherical confidence region, but in general is much worse both from the point of view of productivity (unnecessary multiplication operations, and in normal implementations - factorization), and from the point of view of method stability (matrix multiplication by itself worsens its conditioning). It is sometimes objected that
guaranteed positively defined, but in this case it does not matter. Let's look at the Levenberg-Marquardt method from the perspective of the sequential descent method. In this case, it turns out that we want to use the matrix as a metric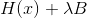 
, and so that she can act in that capacity, the meaning should ensure its positive certainty. Given that 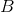positive definite, desired value can always be found - and therefore no need to demand from 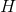positive certainty is not observed.
As a matrix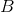 it is not necessary to take a single one, but for a quadratic model of the objective function, specifying an adequate confidence region is no longer as simple as for a linear model. If we take the elliptical region induced by the Hessian, then the method degenerates into Newton's method (well, almost)
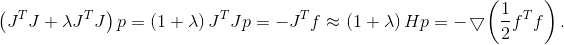
Unless, of course, the Hessian matrix is positive definite. If not, then as before, you can use the corrected Hessian as a metric, or some matrix that is in some sense close to it. There is also a recommendation to use a matrix as a metric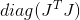
, which by construction is guaranteed to be positive definite. Unfortunately, I do not know at least any rigorous justification for this choice, but it is mentioned quite often as an empirical recommendation.
As an illustration, let's see how the method behaves on the same Rosenbrock function, and we will consider it in two ways - as a simple function written in the form
,
and as a least squares problem
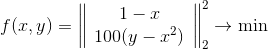
This is how a method with a spherical confidence region behaves.
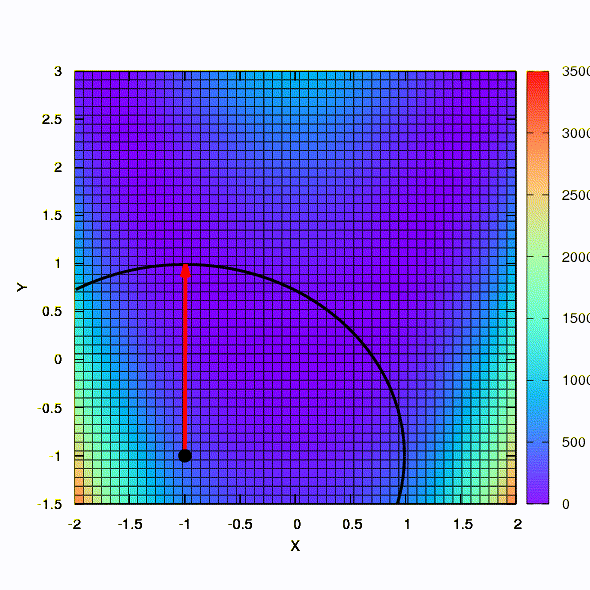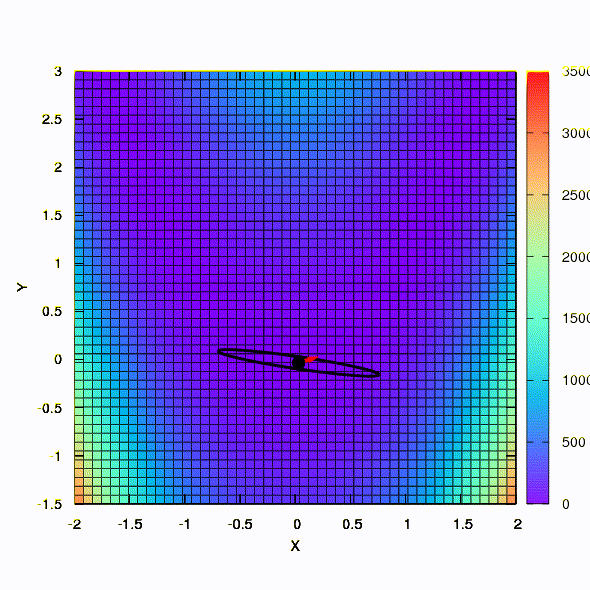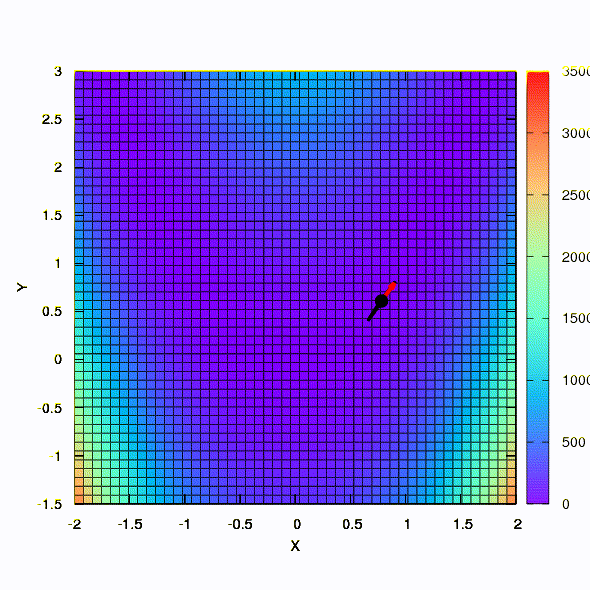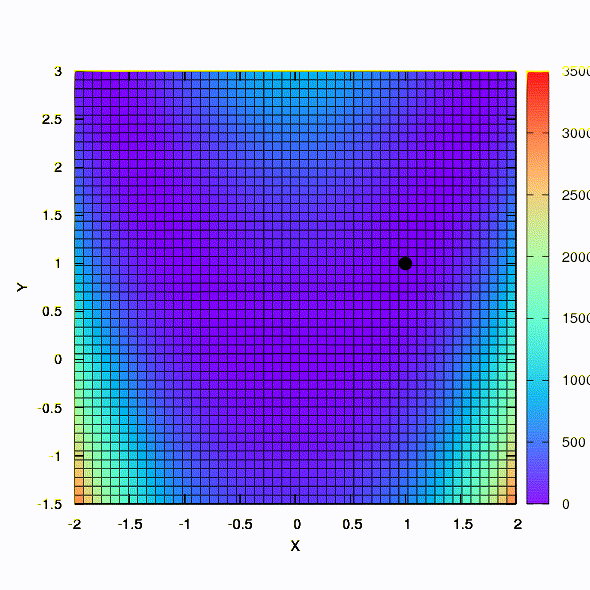
So the same method behaves if the shape of the confidence region is given by a matrix constructed according to the Davidon-Fletcher-Powell rule. There is an effect on convergence, but much more modest than in the similar case when using the linear model of the objective function.
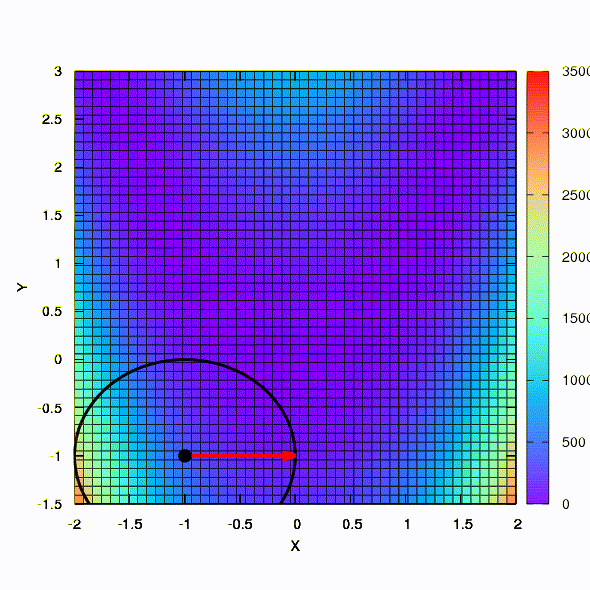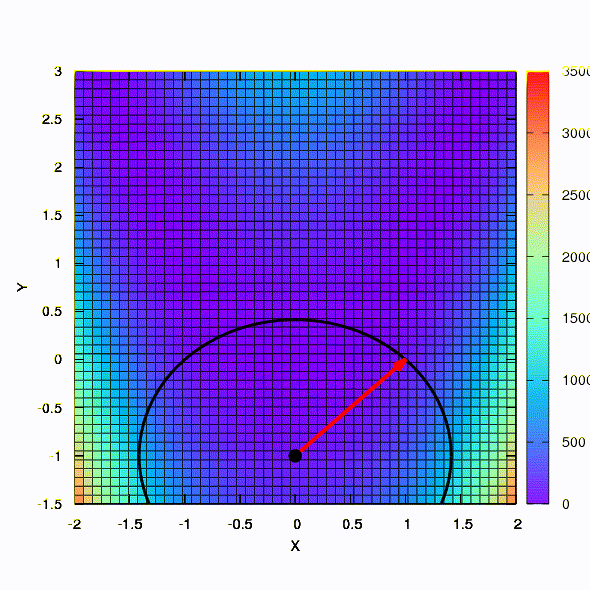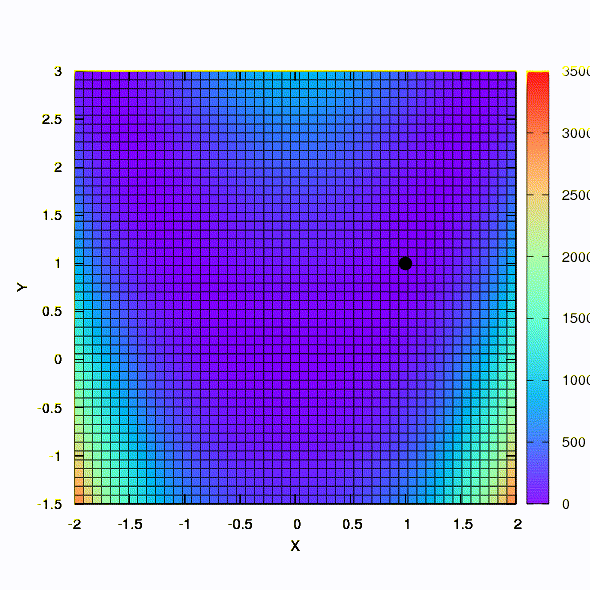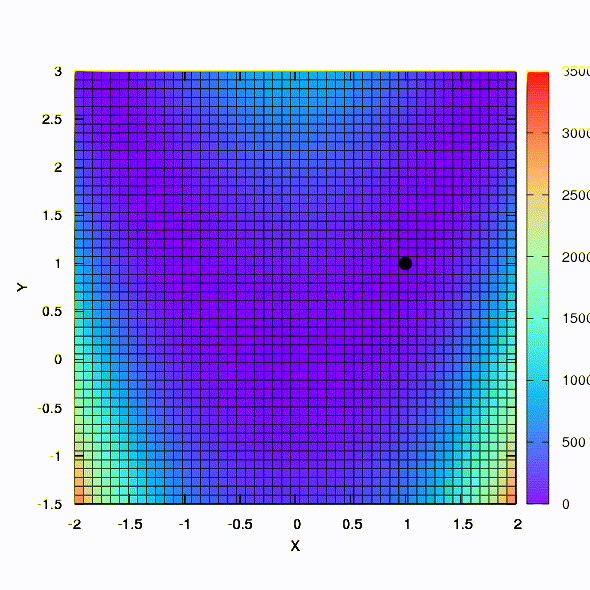
And this is the behavior of the method applied to the least squares problem. It converges in 5 iterations. Just please, do not draw from this conclusion that the second formulation for functions of this kind is always better than the first . This is not so, it just happened in this particular case.
The Levenberg-Marquardt method is, as far as I know, the first method based on the idea of a trusting region. He showed himself very well in practice when solving the least squares problem. The method converges in most cases (seen by me) quite quickly (I said whether it was good or bad in a previous article). However, while minimizing general functions, it is hardly the best option to choose a sphere as a trusted region. In addition, a significant drawback of the method (in its basic formulation, which was described here) is that the size of the confidence region is implicitly set. 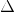The disadvantage is that knowing the meaning we, of course, can count at the current point just by calculating the stride length 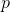. However, when we move to a new point, the same value a completely different value of the confidence region will already correspond. Thus, we lose the ability to determine the “characteristic for the task” value of the confidence region and are forced to determine its size in a new way at each new point. This can be significant when a sufficiently large number of iterations is required for convergence, and calculating the value of a function is expensive. Similar problems are solved in more advanced methods based on the idea of a trusting region.
But this is a completely different story.
Thanks to the valuable comments of Dark_Daiver, I decided that the above should be supplemented with the following remark. Of course, one can arrive at the Levenberg-Marquardt method in a different, purely empirical way. Namely, let us return to the scheme of the sequential descent method described in the previous article and again ask ourselves the question of constructing an adequate metric for the linear model of the objective function.
Suppose that the Hessian matrix at the current point in the search space is not positive definite and cannot serve as a metric (moreover, to check whether this is so, we have neither the ability nor the desire). Denote by
its smallest eigenvalue. Then we can correct the Hessian by simply shifting all its eigenvalues by 
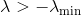. To do this, just add the matrix to the Hessian 
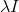. Then the equation determining the direction of descent will take the form
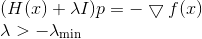
If we have a good bottom grade for , then we can do everything that was done in sequential descent methods. However, if we do not have such an estimate, then taking into account that with an increase the length p will decrease, we can confidently say that there is such a sufficiently large that at the same time 
positive definite and .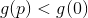
Why I consider such a conclusion of the method not too successful. Firstly, it is not at all obvious that the metric constructed in this way is suitable for practical use. It, of course, uses information about the second derivatives, but it does not follow from anywhere that shifting the eigenvalues by a given value will not make it unusable. As the colleague noted in the comments, it seems obvious that adding a scaled identity matrix to the Hessian matrix leads to the fact that the elliptical confidence region will tend to spherical and here again (as it seems) the problems of jamming in the canyon and other delights of gradient descent and close ones to him methods. But in practice this does not happen. In any case, I have never been able to observe examples illustrating such behavior. In this case, the question arises: but, in fact, why ?
But such a question does not arise if we look at this method not as a special case of descent methods, but as a confidence region method with a quadratic model of the objective function, since the answer is obvious: when lambda increases, we only compress the sphere - the confidence region for our model. Information about the curvature does not go anywhere and is not washed out by anything - we just have to choose the size of the region in which the quadratic model adequately describes the objective function. It follows from this that it is hardly worth expecting a significant effect from a change in the metric, that is, the shape of the confidence region, since all the information we have about the objective function is already taken into account in its model.
And secondly, when considering a method, it is important to understand the main idea that led Marquardt to this method, namely, the idea of a trusting region. Indeed, in the final analysis, only an understanding of the ins and outs of the numerical method will allow us to understand why it works and, more importantly, why it may not work.
And they say about him that he is somewhere in between the gradient descent and the Newton method, whatever that means. Well, it’s sort of sorted out with Newton’s method and its connection with gradient descent. But what do they mean when they utter this profound phrase? Let's try a little sneak.
In his articles, Comrade Levenberg [K. A Method for the Solution of Certain Problems in Last Squares. Quart. Appl. Math. 1944. Vol. 2. P. 164-168.], And after him citizen Marquardt [Marquardt, Donald (1963). "An Algorithm for Least-Squares Estimation of Nonlinear Parameters." SIAM Journal on Applied Mathematics. 11 (2): 431–441.] Considered the least squares problem, which looks like this:
,
which can be written easier in vector form
.
And you can even easier by completely scoring on the least squares. This will not affect the story.
So, the problem is considered
.
Such a problem arises so often that the importance of finding an effective method for solving it can hardly be overestimated. But we will start from another. In a previous article, it was shown that the well-known gradient descent method, and not only it, can be obtained from the following considerations. Let's say we come to some point
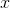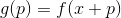in which the minimized function matters . We define an auxiliary function at this point , as well as some of its model 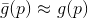. For this model, we pose an auxiliary problem
Where
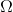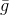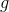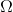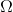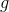- a certain predetermined set of permissible values, chosen so that the problem has a simple solution and the function approximated quite accurately on . This scheme is called the trust region method, and many on which the value of the model function is minimized - the confidence region of this function. For gradient descent, we took , for Newton's method , and as a model for the linear part of the Taylor expansion .
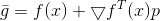Let's see what happens if we complicate the model by taking
.
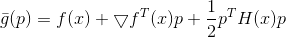We minimize this model function on an elliptic confidence region
(multiplier added for ease of calculation). Applying the Lagrange multiplier method, we obtain the problem
,
whose solution satisfies the equality
or
Here, in contrast to what we saw earlier when using the linear model, the direction p is not only dependent on the metric
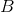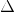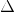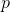, but also on the choice of the size of the trust region , which means the linear search technique is not applicable (at least reasonably). It also turns out to be difficult to explicitly determine corresponding to . However, it is quite obvious that with increasing length will decrease. If in doing so we still impose the condition 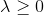, then the step length will be no more than that which Newton's method would give (all-fashionable, without modifications and conditions).
So we can instead for a given
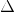look for the right value , do exactly the opposite: find this 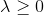under which the condition 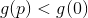. This is a kind of replacement for the late search in this case. Marquardt proposed the following simple procedure:
- if for some value condition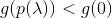
done then repeat 
until 
- if
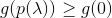then accept 
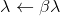and repeat.
Here
and - constants that are method parameters. Multiplication by corresponds to the expansion of the confidence region, and multiplication by 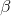- its narrowing.
The specified technique can be applied to any objective function. Note that here the positive definiteness of the Hessian is no longer required, in contrast to the case considered earlier, when the Newton method was presented as a special case of the sequential descent method. Not even its non-degeneracy is required, which in some cases is very important. However, in this case, the price of the direction search increases, since each change
leads to the need to solve a linear system to determine .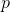
Let's see what happens if we apply this approach to the least squares problem.
Gradient Function
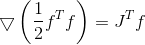her hessian 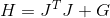where . We substitute and get the following system that determines the direction of the search
.
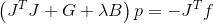It is quite acceptable, but calculating the second derivatives of a vector function can be quite expensive. Marquardt proposed to use the function itself to bypass this problem.
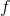, and its linear approximation 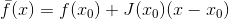at which the matrix turns to zero. If now as 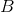take the identity matrix 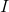, then we obtain the standard form of the Levenberg-Marquardt method for solving the least squares problem:
.
For this method of determining the direction of descent, Marquardt proved the theorem that with aspiration
to infinity direction 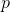tends to anti-gradient. An interested reader can find a rigorous proof in the base article, but I hope that this statement itself has become quite obvious from the logic of the method. To some extent, it justifies the ubiquitous reference to the fact that with an increase in lambda (which for some reason I often call the regularization parameter) we get a gradient descent. Actually, nothing of the kind - we would get it only in the limit, in the very one where the step length tends to zero. It is much more important that for a sufficiently large lambda value, the direction that we get will be the direction of descent , which means we get the global convergence of the method . And here is the second part of the statement that when the lambda tends to zero we get the Newton method, it is clearly true, but only if we accept instead 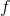its linear approximation .
It would seem that all. We minimize the norm of the vector function in the elliptic metric - we use the Levenberg-Marquardt. We are dealing with a function of a general form and have the ability to calculate the matrix of second derivatives - for Wells, use the general confidence method of the region. But there are perverts ...
Sometimes the Levenberg-Marquardt method to minimize function
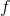they call an expression like this:
.
Everything seems to be the same, but here
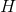- second matrix! derivative functions 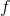. Formally, this has a right to exist, but it is a perversion. And that's why. The same Marquardt in his article proposed a method for solving a system of equations 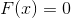by minimizing the function the described method. If as 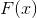take the gradient of the objective function, then we really get the reduced expression. And the perversion is because
the minimization problem generated by the system of nonlinear equations generated by the minimization problem is solved .
Double strike. Such an expression, at least, is not better than the first equation of a spherical confidence region, but in general is much worse both from the point of view of productivity (unnecessary multiplication operations, and in normal implementations - factorization), and from the point of view of method stability (matrix multiplication by itself worsens its conditioning). It is sometimes objected that
guaranteed positively defined, but in this case it does not matter. Let's look at the Levenberg-Marquardt method from the perspective of the sequential descent method. In this case, it turns out that we want to use the matrix as a metric 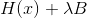, and so that she can act in that capacity, the meaning should ensure its positive certainty. Given that 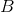positive definite, desired value can always be found - and therefore no need to demand from 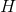positive certainty is not observed.
As a matrix
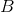it is not necessary to take a single one, but for a quadratic model of the objective function, specifying an adequate confidence region is no longer as simple as for a linear model. If we take the elliptical region induced by the Hessian, then the method degenerates into Newton's method (well, almost)
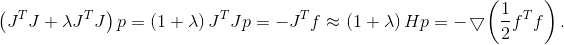
Unless, of course, the Hessian matrix is positive definite. If not, then as before, you can use the corrected Hessian as a metric, or some matrix that is in some sense close to it. There is also a recommendation to use a matrix as a metric
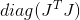, which by construction is guaranteed to be positive definite. Unfortunately, I do not know at least any rigorous justification for this choice, but it is mentioned quite often as an empirical recommendation.
As an illustration, let's see how the method behaves on the same Rosenbrock function, and we will consider it in two ways - as a simple function written in the form
,
and as a least squares problem
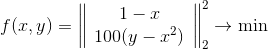
This is how a method with a spherical confidence region behaves.
So the same method behaves if the shape of the confidence region is given by a matrix constructed according to the Davidon-Fletcher-Powell rule. There is an effect on convergence, but much more modest than in the similar case when using the linear model of the objective function.
And this is the behavior of the method applied to the least squares problem. It converges in 5 iterations. Just please, do not draw from this conclusion that the second formulation for functions of this kind is always better than the first . This is not so, it just happened in this particular case.
Conclusion
The Levenberg-Marquardt method is, as far as I know, the first method based on the idea of a trusting region. He showed himself very well in practice when solving the least squares problem. The method converges in most cases (seen by me) quite quickly (I said whether it was good or bad in a previous article). However, while minimizing general functions, it is hardly the best option to choose a sphere as a trusted region. In addition, a significant drawback of the method (in its basic formulation, which was described here) is that the size of the confidence region is implicitly set. The disadvantage is that knowing the meaning
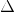we, of course, can count at the current point just by calculating the stride length 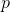. However, when we move to a new point, the same value a completely different value of the confidence region will already correspond. Thus, we lose the ability to determine the “characteristic for the task” value of the confidence region and are forced to determine its size in a new way at each new point. This can be significant when a sufficiently large number of iterations is required for convergence, and calculating the value of a function is expensive. Similar problems are solved in more advanced methods based on the idea of a trusting region.
But this is a completely different story.
Addition
Thanks to the valuable comments of Dark_Daiver, I decided that the above should be supplemented with the following remark. Of course, one can arrive at the Levenberg-Marquardt method in a different, purely empirical way. Namely, let us return to the scheme of the sequential descent method described in the previous article and again ask ourselves the question of constructing an adequate metric for the linear model of the objective function.
Suppose that the Hessian matrix at the current point in the search space is not positive definite and cannot serve as a metric (moreover, to check whether this is so, we have neither the ability nor the desire). Denote by
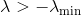its smallest eigenvalue. Then we can correct the Hessian by simply shifting all its eigenvalues by . To do this, just add the matrix to the Hessian 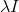. Then the equation determining the direction of descent will take the form
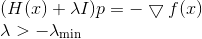
If we have a good bottom grade for
, then we can do everything that was done in sequential descent methods. However, if we do not have such an estimate, then taking into account that with an increase the length p will decrease, we can confidently say that there is such a sufficiently large that at the same time positive definite and .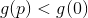
Why I consider such a conclusion of the method not too successful. Firstly, it is not at all obvious that the metric constructed in this way is suitable for practical use. It, of course, uses information about the second derivatives, but it does not follow from anywhere that shifting the eigenvalues by a given value will not make it unusable. As the colleague noted in the comments, it seems obvious that adding a scaled identity matrix to the Hessian matrix leads to the fact that the elliptical confidence region will tend to spherical and here again (as it seems) the problems of jamming in the canyon and other delights of gradient descent and close ones to him methods. But in practice this does not happen. In any case, I have never been able to observe examples illustrating such behavior. In this case, the question arises: but, in fact, why ?
But such a question does not arise if we look at this method not as a special case of descent methods, but as a confidence region method with a quadratic model of the objective function, since the answer is obvious: when lambda increases, we only compress the sphere - the confidence region for our model. Information about the curvature does not go anywhere and is not washed out by anything - we just have to choose the size of the region in which the quadratic model adequately describes the objective function. It follows from this that it is hardly worth expecting a significant effect from a change in the metric, that is, the shape of the confidence region, since all the information we have about the objective function is already taken into account in its model.
And secondly, when considering a method, it is important to understand the main idea that led Marquardt to this method, namely, the idea of a trusting region. Indeed, in the final analysis, only an understanding of the ins and outs of the numerical method will allow us to understand why it works and, more importantly, why it may not work.
All Articles