We design a space rocket from scratch. Part 5 - Kepler's First Law

Content

Part 1 - The task of two bodies

Part 2 - Semi-solution of the two-body problem

Part 3 - Already almost-solution of the two-body problem

Part 4 - Kepler's Second Law

Hello to all readers! Immediately proceed to continue without unnecessary ranting. Last time we stopped at:

d d o t r h o = - d f r a c m u r h o^{2} + d f r a c h^{2} r h o^{3}

$\ ddot {\ rho} = - \ dfrac {\ mu} {\ rho ^ {2}} + \ dfrac {h ^ {2}} {\ rho ^ {3}}$

This is a second-order differential equation, where, as an unknown function, is the length of the radius of a time-dependent vector. Here

h^{2} g e q 0, m u = G (m_{1} + m_{2}) > 0.

$h ^ {2} \ geq0, \ mu = G (m_ {1} + m_ {2})> 0.$

h,

$h,$ as we recall, it can be zero in the case of rectilinear motion along the radius vector. This case is too simple, we won’t even consider it, and whoever wants to can equalize in the equation to zero and solve it further.

Here we try to solve for

h n e q 0.

$h \ neq0.$ The first thing that comes to mind (it came to mine when I first saw this equation) is that it’s not here

d o t r h o

$\ dot {\ rho}$ well of course and

t .

$t.$ And in such cases (special) it is possible to carry out further replacement, which reduces the order of the equation to the first.

In the general case, a second-order equation can be written as:

F (t, r h o, d o t r h o, d d o t r h o) = 0

$F (t, \ rho, \ dot {\ rho}, \ ddot {\ rho}) = 0$

In our case, the equation is simpler when:

F (r h o, d d o t r h o) = 0

$F (\ rho, \ ddot {\ rho}) = 0$

And in such cases, you can make a substitution that reduces the order of the equation:

d o t r h o = z (r h o),

$\ dot {\ rho} = z (\ rho),$

Where

z

$z$ - a new unknown function, but which does not depend directly on time, but on

r h o .

$\ rho.$ Then:

d d o t r h o = d f r a c d z d r h o d f r a c d r h o d t = z^{^{'}} d o t r h o = z^{^{'}} z

$\ ddot {\ rho} = \ dfrac {dz} {d \ rho} \ dfrac {d \ rho} {dt} = z ^ {'} \ dot {\ rho} = z ^ {'} z$

Here we differentiated as a complex function, and then the derivative

z

$z$ by

r h o .

$\ rho.$ Now everything is ready, and you can substitute:

z^{^{'}} z = - d f r a c m u r h o^{2} + d f r a c h^{2} r h o^{3}

$z ^ {'} z = - \ dfrac {\ mu} {\ rho ^ {2}} + \ dfrac {h ^ {2}} {\ rho ^ {3}}$

First order equation but relatively

r h o,

$\ rho,$ instead of time. And with shared variables:

d f r a c d z d r h o z = - d f r a c m u r h o^{2} + d f r a c h^{2} r h o^{3}

$\ dfrac {dz} {d \ rho} z = - \ dfrac {\ mu} {\ rho ^ {2}} + \ dfrac {h ^ {2}} {\ rho ^ {3}}$

z d z = l e f t (- d f r a c m u r h o^{2} + d f r a c h^{2} r h o^{3} r i g h t) d r h o

$zdz = \ left (- \ dfrac {\ mu} {\ rho ^ {2}} + \ dfrac {h ^ {2}} {\ rho ^ {3}} \ right) d \ rho$

Integrating is not difficult:

d f r a c z^{2} 2 = d f r a c m u r h o - d f r a c h^{2} 2 r h o^{2} + d f r a c C 2

$\ dfrac {z ^ {2}} {2} = \ dfrac {\ mu} {\ rho} - \ dfrac {h ^ {2}} {2 \ rho ^ {2}} + \ dfrac {C} { 2}$

Well added gender constants, what's the difference? But then it’s easier to live:

z^{2} = d f r a c 2 m u r h o - d f r a c h^{2} r h o^{2} + C = d f r a c 2 m u r h o - h^{2} + C r h o^{2} r h o^{2}

$z ^ {2} = \ dfrac {2 \ mu} {\ rho} - \ dfrac {h ^ {2}} {\ rho ^ {2}} + C = \ dfrac {2 \ mu \ rho - h ^ {2} + C \ rho ^ {2}} {\ rho ^ {2}}$

It's time to remember what is

z

$z$ :

d o t {r h o}^{2} = d f r a c 2 m u r h o - h^{2} + C r h o^{2} r h o^{2}

$\ dot {\ rho} ^ {2} = \ dfrac {2 \ mu \ rho - h ^ {2} + C \ rho ^ {2}} {\ rho ^ {2}}$

And extract the root:

d o t r h o = p m s q r t d f r a c 2 m u r h o - h^{2} + C r h o^{2} r h o^{2} = p m d f r a c s q r t C r h o^{2} + 2 m u r h o - h^{2} r h o

$\ dot {\ rho} = \ pm \ sqrt {\ dfrac {2 \ mu \ rho - h ^ {2} + C \ rho ^ {2}} {\ rho ^ {2}}} = \ pm \ dfrac {\ sqrt {C \ rho ^ {2} + 2 \ mu \ rho - h ^ {2}}} {\ rho}$

The equation is again with separable variables, and even the integral seems to be taken in elementary functions:

i n t d f r a c r h o d r h o s q r t C r h o^{2} + 2 m u r h o - h^{2} = p m i n t d t

$\ int \ dfrac {\ rho d \ rho} {\ sqrt {C \ rho ^ {2} + 2 \ mu \ rho - h ^ {2}}} = \ pm \ int dt$

And everything would be fine, but the problem is that if we decide, we get an inverse relationship, that is, time on the radius:

t = f (r h o)

$t = f (\ rho)$

But I would like the opposite:

r h o = f^{- 1} (t)

$\ rho = f ^ {- 1} (t)$

Yes, and this

p m

$\ pm$ - think which branch to choose. But this is not the worst, you will need to consider different cases of constant ratios under the root:

C > 0, C < 0, C = 0 . . .

$C> 0, C <0, C = 0 ...$

You can, of course, drive into wolframalpha and figure out what will happen:

This is just fear and horror, and you can not even dream of finding the inverse elementary function. But we still need to look for the angle:

d o t p h i = d f r a c h r h o^{2}

$\ dot {\ phi} = \ dfrac {h} {\ rho ^ {2}}$

p h i = h i n t d f r a c d t r h o^{2} = h i n t d f r a c d t l e f t (f^{- 1} (t) r i g h t)^{2}

$\ phi = h \ int \ dfrac {dt} {\ rho ^ {2}} = h \ int \ dfrac {dt} {\ left (f ^ {- 1} (t) \ right) ^ {2}}$

Too dreary business. And even the ability to count integrals from inverse functions will not save us most likely.

Ability to count integrals of inverse functions

i n t d f r a c d t l e f t (f^{- 1} (t) r i g h t)^{2} = b e g i n v m a t r i x y = f^{- 1} (t) f (y) = t d t = f^{^{'}} (y) d y e n d v m a t r i x = i n t d f r a c f^{^{'}} (y) d y y^{2}

$\ int \ dfrac {dt} {\ left (f ^ {- 1} (t) \ right) ^ {2}} = \ begin {vmatrix} y = f ^ {- 1} (t) \\ f ( y) = t \\ dt = f ^ {'} (y) dy \ end {vmatrix} = \ int \ dfrac {f ^ {'} (y) dy} {y ^ {2}}$

By the way, you can notice some property for the angle

p h i

$\ phi$ here from this equality:

d o t p h i = d f r a c h r h o^{2}

$\ dot {\ phi} = \ dfrac {h} {\ rho ^ {2}}$

r h o^{2} > 0

$\ rho ^ {2}> 0$ - this thing is always greater than zero. It is more correct from the point of view of mathematics to say: it is more or equal to zero, but from the physical point of view - only more. After all, our bodies are not material points. So they can never get closer to zero distance. That is, their centers of mass will never coincide, otherwise they would have to pass through each other. So who is afraid of dividing by zero - do not be afraid.

So what am I talking about, oh yes.

h

$h$ also always greater than or less than zero, or zero. After all, this is a constant value (by the way, when zero - then the angle is constant and the movement along the radius of the vector was verified again). And this means that the derivative of the angle is constant in sign throughout the movement:

d o t p h i > 0

$\ dot {\ phi}> 0$

d o t p h i < 0

$\ dot {\ phi} <0$

depending on the sign

h

$h$ .

In other words, the corner itself

p h i

$\ phi$ Is a strictly monotonic function. Who does not remember how it is, here is a clear picture:

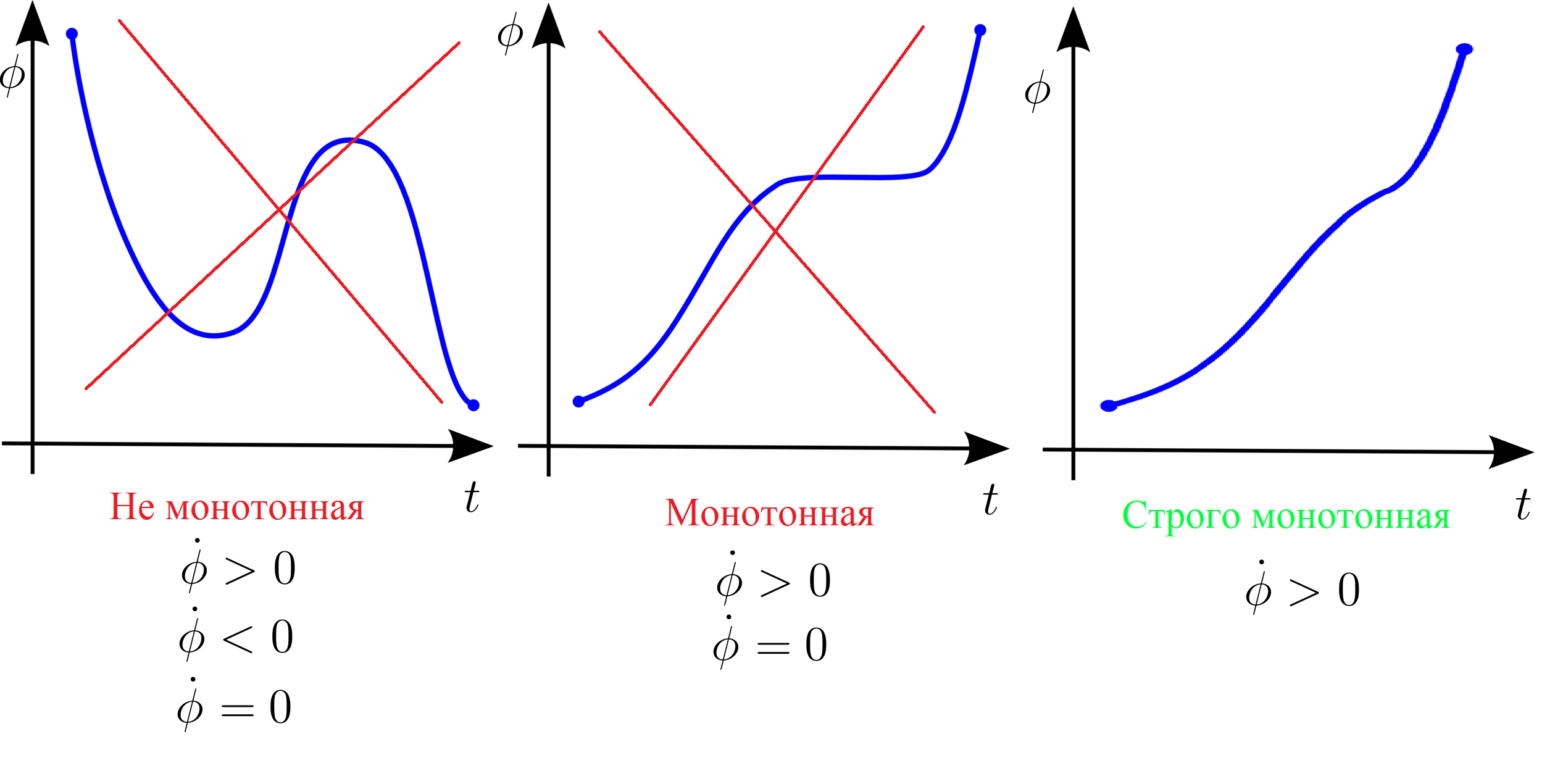
Monotonic and nonmonotonic function

This fact confirms what we saw in the numerical simulation. The body always moves in one direction. It never stops (the derivative is zero) and does not start spinning in the opposite direction (the derivative changes sign).

Accordingly, the trajectories may and may not be as follows:

Blue - possible trajectories, red - impossible (in polar coordinates)

Well, animations are not superfluous:

Derivative

$\ dot {\ phi}$ changes sign. We definitely won’t have such decisions.

By the way, ellipses, hyperbolas and parabolas (sections of a cone by a plane) are very possible. We saw this last time, numerically counting.

I wanted to make my educational program on conic sections, but today I became lazy, and I want to publish the article already. Maybe I'll do it sometime in the future. In the meantime, you can limit yourself to this: Dundelen balls - this is where ellipses have tricks growing.

In polar coordinates, conics can be defined as follows (with the center in one of the foci and the zero direction along the main axis):

r h o = d f r a c l 1 + e c o s (p h i),

$\ rho = \ dfrac {l} {1 + e \ cos (\ phi)},$

Where

e

$e$ denotes eccentricity, and

l

$l$ focal parameter.

And lo and behold, all three types of conics are defined by one equation, and only the eccentricity determines what the conic will become today.

Ellipse (

e < 1

$e <1$ ):

r h o = d f r a c 1 1 + 0.5 c o s (p h i)

$\ rho = \ dfrac {1} {1 + 0.5 \ cos (\ phi)}$

Ellipse

Parabola (

e = 1

$e = 1$ ):

r h o = d f r a c 1 1 + c o s (p h i)

$\ rho = \ dfrac {1} {1 + \ cos (\ phi)}$

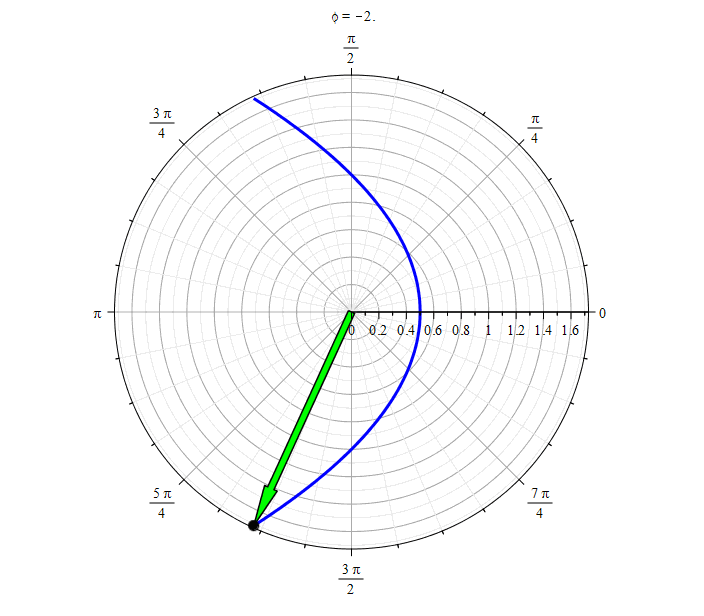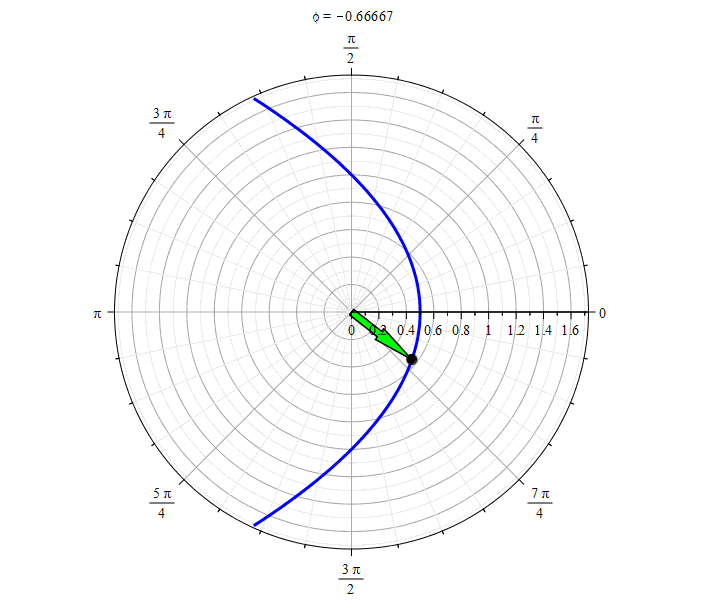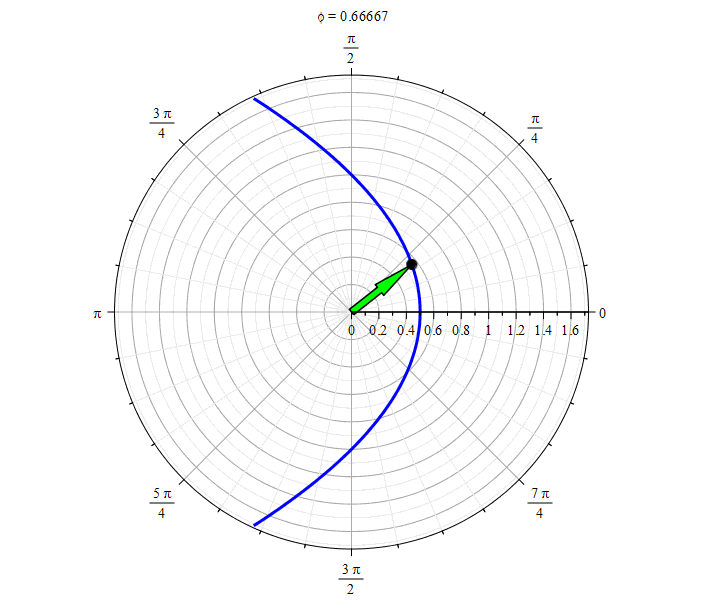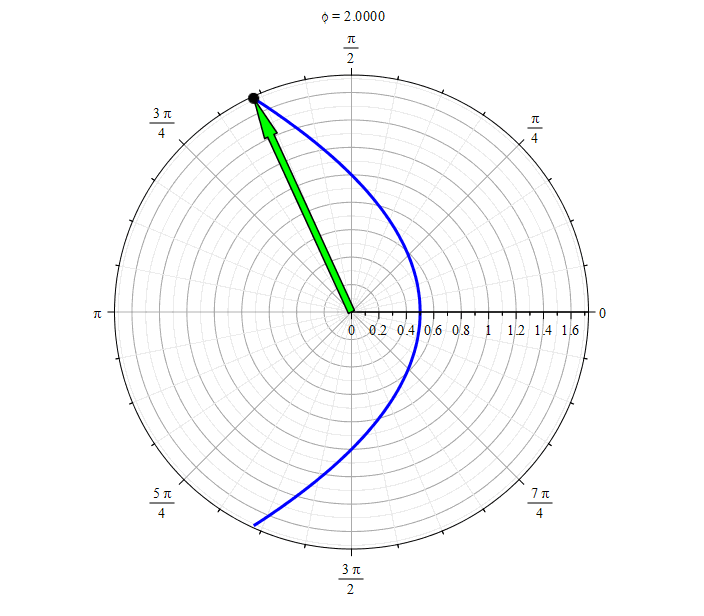
Parabola

Hyperbola (

e > 1

$e> 1$ ):

r h o = d f r a c 1 1 + 1.5 c o s (p h i)

$\ rho = \ dfrac {1} {1 + 1.5 \ cos (\ phi)}$

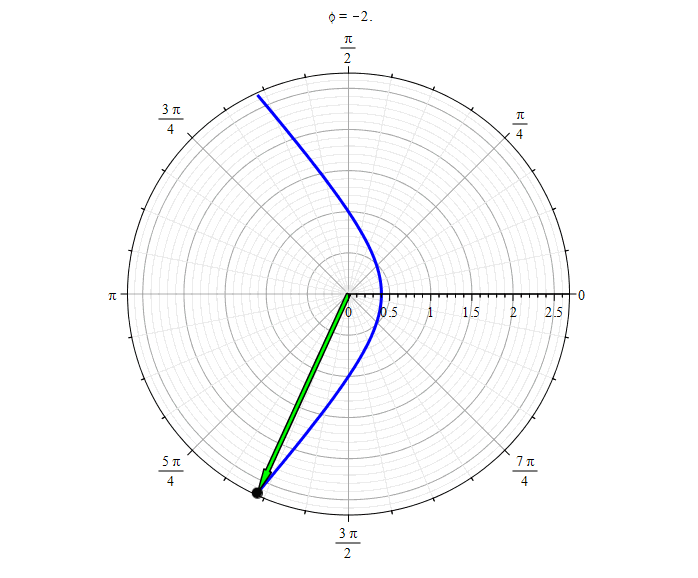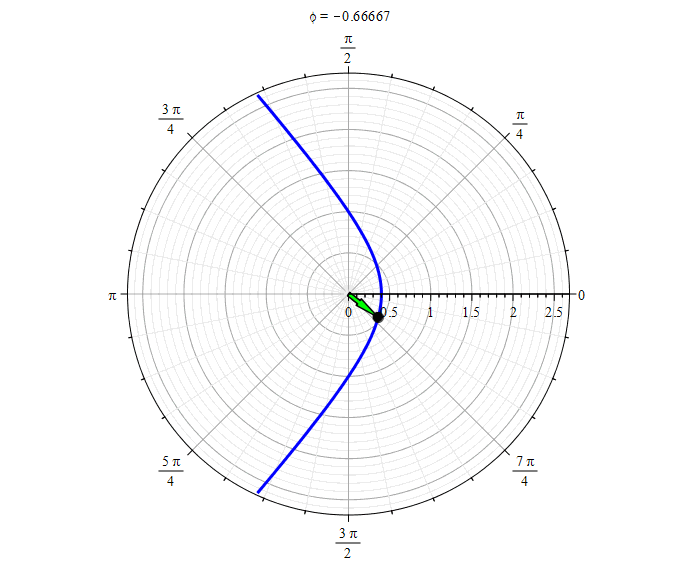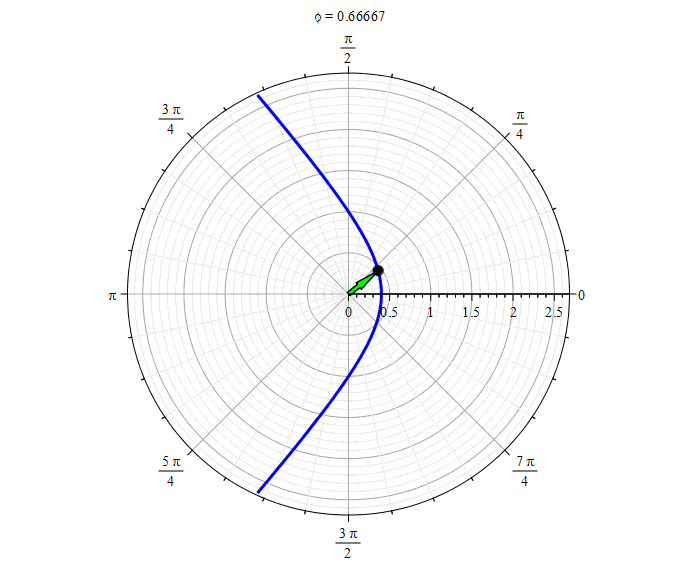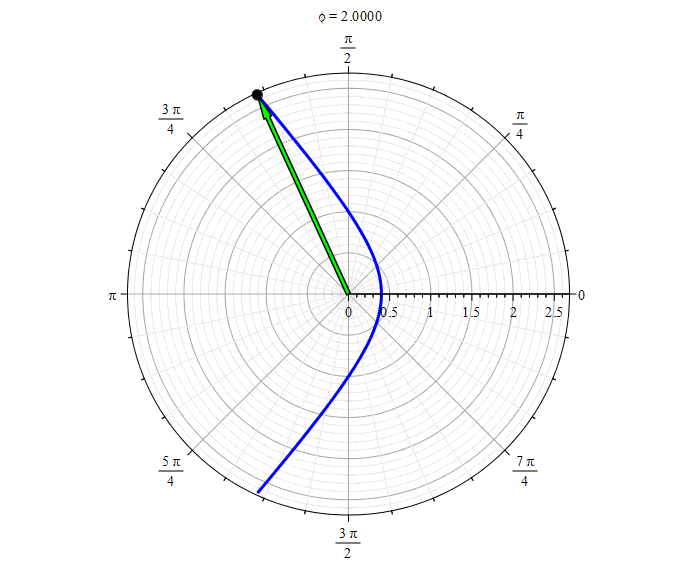
Hyperbola

Everything is very similar to the satellite trajectories obtained by numerical simulation ...

As you can see here

r h o = r h o (p h i)

$\ rho = \ rho (\ phi)$ - radius as a function of angle. And the expressions are pretty simple. So maybe it makes sense to first find the dependence of the radius on the angle, and then the angle as a function of time? You can try and test our hypothesis that solutions are conic.

Recall that we have:

\ begin {equation *}

\ begin {cases}

\ dot {\ phi} = \ dfrac {h} {\ rho ^ {2}},

\\

\ dot {\ rho} = \ pm \ dfrac {\ sqrt {C \ rho ^ {2} + 2 \ mu \ rho - h ^ {2}}} {\ rho}.

\ end {cases}

\ end {equation *}

By dividing one into another, you can get rid of

d t

$dt$ :

d f r a c d p h i d t d f r a c d t d r h o = p m d f r a c h r h o^{2} d f r a c r h o s q r t C r h o^{2} + 2 m u r h o - h^{2},

$\ dfrac {d \ phi} {dt} \ dfrac {dt} {d \ rho} = \ pm \ dfrac {h} {\ rho ^ {2}} \ dfrac {\ rho} {\ sqrt {C \ rho ^ {2} + 2 \ mu \ rho - h ^ {2}}},$

d f r a c d p h i d r h o = d f r a c h r h o s q r t C r h o^{2} + 2 m u r h o - h^{2}

$\ dfrac {d \ phi} {d \ rho} = \ dfrac {h} {\ rho \ sqrt {C \ rho ^ {2} + 2 \ mu \ rho - h ^ {2}}}$

But again it turns out uncomfortable, on the contrary:

i n t d p h i = h i n t d f r a c d r h o r h o s q r t C r h o^{2} + 2 m u r h o - h^{2}

$\ int d \ phi = h \ int \ dfrac {d \ rho} {\ rho \ sqrt {C \ rho ^ {2} + 2 \ mu \ rho - h ^ {2}}}$

Of course, this integral can be taken, and even, most likely, then it will not be possible to find the inverse function of labor. But there is a simpler way to find addiction

r h o = r h o (p h i) .

$\ rho = \ rho (\ phi).$

We assume that the solution will look like this:

r h o = d f r a c l 1 + e c o s (p h i),

$\ rho = \ dfrac {l} {1 + e \ cos (\ phi)},$

Here is the equation:

d d o t r h o = - d f r a c m u r h o^{2} + d f r a c h^{2} r h o^{3}

$\ ddot {\ rho} = - \ dfrac {\ mu} {\ rho ^ {2}} + \ dfrac {h ^ {2}} {\ rho ^ {3}}$

But the time derivative, though. And we would be in the corner. Nothing prevents just making a complex function:

r h o = r h o (p h i (t))

$\ rho = \ rho (\ phi (t))$

continue to differentiate a couple of times, while using the facts we have already obtained (

r h o^{2} d o t p h i = h

$\ rho ^ {2} \ dot {\ phi} = h$ )

But before that, the equation itself and the proposed solution itself asks to make such a replacement:

r h o = d f r a c 1 u

$\ rho = \ dfrac {1} {u}$

Then the function itself

u

$u$ will be like this:

u = a + b c o s (p h i)

$u = a + b \ cos (\ phi)$

And these are the solutions of such elementary diffurs:

d d o t u + k u = f

$\ ddot {u} + k u = f$

That is, by making a sequential change:

r h o = d f r a c 1 u,

$\ rho = \ dfrac {1} {u},$

u = u (p h i)

$u = u (\ phi)$

It is hoped that the equation will be reduced to a very simple one.

Proceed:

r h o = d f r a c 1 u,

$\ rho = \ dfrac {1} {u},$

d o t r h o = d f r a c d d t u^{- 1} = - d f r a c 1 u^{2} d o t u = - d f r a c d o t u u^{2},

$\ dot {\ rho} = \ dfrac {d} {dt} u ^ {- 1} = - \ dfrac {1} {u ^ {2}} \ dot {u} = - \ dfrac {\ dot {u }} {u ^ {2}},$

d d o t r h o = - d f r a c d d t l e f t (d f r a c 1 u^{2} d o t u r i g h t) = - l e f t (d f r a c d u^{- 2} d t d o t u + d f r a c 1 u^{2} d d o t u r i g h t) =

$\ ddot {\ rho} = - \ dfrac {d} {dt} \ left (\ dfrac {1} {u ^ {2}} \ dot {u} \ right) = - \ left (\ dfrac {du ^ {-2}} {dt} \ dot {u} + \ dfrac {1} {u ^ {2}} \ ddot {u} \ right) =$

= - l e f t (- 2 d f r a c 1 u^{3} d o t u^{2} + d f r a c 1 u^{2} d d o t u r i g h t) = - d f r a c d d o t u u^{2} + 2 d f r a c d o t u^{2} u^{3}

$= - \ left (-2 \ dfrac {1} {u ^ {3}} \ dot {u} ^ {2} + \ dfrac {1} {u ^ {2}} \ ddot {u} \ right) = - \ dfrac {\ ddot {u}} {u ^ {2}} + 2 \ dfrac {\ dot {u} ^ {2}} {u ^ {3}}$

Substituting the source will be like this:

- d f r a c d d o t u u^{2} + 2 d f r a c d o t u^{2} u^{3} = - m u u^{2} + h^{2} u^{3}

$- \ dfrac {\ ddot {u}} {u ^ {2}} + 2 \ dfrac {\ dot {u} ^ {2}} {u ^ {3}} = - \ mu u ^ {2} + h ^ {2} u ^ {3}$

And let's continue, let now:

u = u (p h i),

$u = u (\ phi),$

d o t u = d f r a c d u d p h i d f r a c d p h i d t = u^{^{'}} d o t p h i = b e g i n v m a t r i x d o t p h i = d f r a c h r h o^{2} d o t p h i = h u^{2} e n d v m a t r i x = h u^{2} u^{^{'}},

$\ dot {u} = \ dfrac {du} {d \ phi} \ dfrac {d \ phi} {dt} = u ^ {'} \ dot {\ phi} = \ begin {vmatrix} \ dot {\ phi } = \ dfrac {h} {\ rho ^ {2}} \\ \ dot {\ phi} = hu ^ {2} \ end {vmatrix} = hu ^ {2} u ^ {'},$

d d o t u = d f r a c d d t (h u^{2} u^{^{'}}) = h l e f t (d f r a c d u^{2} d t u^{^{'}} + u^{2} d f r a c d u^{^{'}} d t r i g h t) =

$\ ddot {u} = \ dfrac {d} {dt} (hu ^ {2} u ^ {'}) = h \ left (\ dfrac {du ^ {2}} {dt} u ^ {'} + u ^ {2} \ dfrac {du ^ {'}} {dt} \ right) =$

= h l e f t (2 u d f r a c d u d t u^{^{'}} + u^{2} d f r a c d u^{^{'}} d p h i d f r a c d p h i d t r i g h t) = h l e f t (2 u d o t u u^{^{'}} + u^{2} u^{^{″}} d o t p h i r i g h t) =

$= h \ left (2u \ dfrac {du} {dt} u ^ {'} + u ^ {2} \ dfrac {du ^ {'}} {d \ phi} \ dfrac {d \ phi} {dt} \ right) = h \ left (2u \ dot {u} u ^ {'} + u ^ {2} u ^ {' '} \ dot {\ phi} \ right) =$

= h \ left (2uhu ^ {2} u ^ {'} u ^ {'} + u ^ {2} u ^ {'}} hu ^ {2} \ right) = h ^ {2} \ left ( 2u ^ {3} (u ^ {'}) ^ {2} + u ^ {4} u ^ {' '} \ right)

$= h \ left (2uhu ^ {2} u ^ {'} u ^ {'} + u ^ {2} u ^ {'}} hu ^ {2} \ right) = h ^ {2} \ left ( 2u ^ {3} (u ^ {'}) ^ {2} + u ^ {4} u ^ {' '} \ right)$

Yes, you need to work a little harder to differentiate everything and not to make a mistake, but nevertheless to differentiate it is not to integrate. Anyway, everything can be entrusted to the machine, it will correctly take the derivative. Machines, of course, can integrate, but not always. But to differentiate anything. Integration after all is creativity and IMHO will always remain it (Breaking - not building).

In the end, what we have:

- d f r a c d d o t u u^{2} + 2 d f r a c d o t u^{2} u^{3} = - m u u^{2} + h^{2} u^{3},

$- \ dfrac {\ ddot {u}} {u ^ {2}} + 2 \ dfrac {\ dot {u} ^ {2}} {u ^ {3}} = - \ mu u ^ {2} + h ^ {2} u ^ {3},$

- d f r a c h^{2} l e f t (2 u^{3} (u^{^{'}})^{2} + u^{4} u^{^{″}} r i g h t) u^{2} + 2 d f r a c (h u^{2} u^{^{'}})^{2} u^{3} = - m u u^{2} + h^{2} u^{3},

$- \ dfrac {h ^ {2} \ left (2u ^ {3} (u ^ {'}) ^ {2} + u ^ {4} u ^ {' '} \ right)} {u ^ {2 }} + 2 \ dfrac {(hu ^ {2} u ^ {'}) ^ {2}} {u ^ {3}} = - \ mu u ^ {2} + h ^ {2} u ^ {3 },$

- 2 h^{2} u (u^{^{'}})^{2} - h^{2} u^{2} u^{^{″}} + 2 h^{2} u (u^{^{'}})^{2} = - m u u^{2} + h^{2} u^{3},

$-2h ^ {2} u (u ^ {'}) ^ {2} - h ^ {2} u ^ {2} u ^ {' '} + 2h ^ {2} u (u ^ {'}) ^ {2} = - \ mu u ^ {2} + h ^ {2} u ^ {3},$

- h^{2} u^{2} u^{^{″}} = - m u u^{2} + h^{2} u^{3},

$- h ^ {2} u ^ {2} u ^ {''} = - \ mu u ^ {2} + h ^ {2} u ^ {3},$

- h^{2} u^{^{″}} = - m u + h^{2} u,

$- h ^ {2} u ^ {''} = - \ mu + h ^ {2} u,$

u^{^{″}} = d f r a c m u h^{2} - u,

$u ^ {''} = \ dfrac {\ mu} {h ^ {2}} - u,$

u^{^{″}} + u = d f r a c m u h^{2} .

$u ^ {''} + u = \ dfrac {\ mu} {h ^ {2}}.$

Well, will we solve this equation?

This is a linear diff. second-order equation (second derivative) is heterogeneous (not zero on the right). But the heterogeneity does not complicate the decision process too much for us, since the constant on the right is also always greater than zero (h is not equal to zero, who wanted to consider this case at the very beginning, and for this it was not necessary to do all the above).

The standard method of solution, but for prettiness, we write everything down, do not miss anything:

u^{^{″}} + u = 0,

$u ^ {''} + u = 0,$

l a m b d a^{2} + 1 = 0,

$\ lambda ^ {2} + 1 = 0,$

l a m b d a = p m i,

$\ lambda = \ pm i,$

So the solution will be:

u_{o} = C_{1} s i n (p h i) + C_{2} c o s (p h i),

$u_ {o} = C_ {1} sin (\ phi) + C_ {2} cos (\ phi),$

The general decision will be as a sum of homogeneous and particular. You can search for a particular in the form of a constant:

u_{t e x t h} = K,

$u _ {\ text {h}} = K,$

Then the general solution:

u = C_{1} s i n (p h i) + C_{2} c o s (p h i) + K

$u = C_ {1} sin (\ phi) + C_ {2} cos (\ phi) + K$

Differentiating twice and substituting in the original equation, we find the constant of the particular solution:

u^{^{″}} = - C_{1} s i n (p h i) - C_{2} c o s (p h i)

$u ^ {''} = -C_ {1} sin (\ phi) - C_ {2} cos (\ phi)$

u^{^{″}} + u = - C_{1} s i n (p h i) - C_{2} c o s (p h i) + C_{1} s i n (p h i) + C_{2} c o s (p h i) + K = d f r a c m u h^{2}

$u ^ {''} + u = -C_ {1} sin (\ phi) - C_ {2} cos (\ phi) + C_ {1} sin (\ phi) + C_ {2} cos (\ phi) + K = \ dfrac {\ mu} {h ^ {2}}$

K = d f r a c m u h^{2}

$K = \ dfrac {\ mu} {h ^ {2}}$

Well, it just so happened that this constant is the right side of our equation. Eventually:

u = C_{1} s i n (p h i) + C_{2} c o s (p h i) + d f r a c m u h^{2}

$u = C_ {1} sin (\ phi) + C_ {2} cos (\ phi) + \ dfrac {\ mu} {h ^ {2}}$

Here we have two arbitrary constants (the equation is still of the second order), which are determined from the initial conditions. But the problem is that we expected to find a solution in this form (ellipses, hyperbolas, parabolas):

u = a + b c o s (p h i)

$u = a + b \ cos (\ phi)$

Same? Well, it’s okay, anyone who is familiar with trigonometry will easily record everything as he wishes (a famous trick):

C_{1} s i n (p h i) + C_{2} c o s (p h i) = s q r t C_{1}^{2} + C_{2}^{2} l e f t (d f r a c C_{1} s q r t C_{1}^{2} + C_{2}^{2} s i n (p h i) + d f r a c C_{2} s q r t C_{1}^{2} + C_{2}^{2} c o s (p h i) r i g h t) =

$C_ {1} sin (\ phi) + C_ {2} cos (\ phi) = \ sqrt {C_ {1} ^ {2} + C_ {2} ^ {2}} \ left (\ dfrac {C_ { 1}} {\ sqrt {C_ {1} ^ {2} + C_ {2} ^ {2}}} sin (\ phi) + \ dfrac {C_ {2}} {\ sqrt {C_ {1} ^ { 2} + C_ {2} ^ {2}}} cos (\ phi) \ right) =$

= s q r t C_{1}^{2} + C_{2}^{2} l e f t (s i n (o m e g a) s i n (p h i) + c o s (o m e g a) c o s (p h i) r i g h t) = A c o s (p h i - o m e g a),

$= \ sqrt {C_ {1} ^ {2} + C_ {2} ^ {2}} \ left (sin (\ omega) sin (\ phi) + cos (\ omega) cos (\ phi) \ right) = A \ cos (\ phi - \ omega),$

Where

A, o m e g a

$A, \ omega$ - two arbitrary constants expressed through old

C_{1}, C_{2}

$C_ {1}, C_ {2}$ in a simple way. And in general this does not matter to us, because these are constants.

Thus, we have a solution, in a more or less expected form:

u = d f r a c m u h^{2} + A c o s (p h i - o m e g a)

$u = \ dfrac {\ mu} {h ^ {2}} + A \ cos (\ phi - \ omega)$

And unknown constants are also expected, for this we need the value of the function at the starting point, as well as the derivative:

\ begin {equation *}

\ begin {cases}

u (0) = u_ {0},

\\

u ^ {'} (0) = u ^ {'} _ {0}.

\ end {cases}

\ end {equation *}

Do not forget also that the dependence here is on the angle, and not on time:

u (0) = u (p h i = 0)

$u (0) = u (\ phi = 0)$

Need derivative, please:

u^{^{'}} = - A s i n (p h i - o m e g a)

$u ^ {'} = -A \ sin (\ phi - \ omega)$

And a system for finding arbitrary constants:

\ begin {equation *}

\ begin {cases}

\ dfrac {\ mu} {h ^ {2}} + A \ cos (0 - \ omega) = u_ {0},

\\

-A \ sin (0 - \ omega) = u ^ {'} _ {0}.

\ end {cases}

\ end {equation *}

\ begin {equation *}

\ begin {cases}

A \ cos (\ omega) = u_ {0} - \ dfrac {\ mu} {h ^ {2}} = a,

\\

A \ sin (\ omega) = u ^ {'} _ {0} = b.

\ end {cases}

\ end {equation *}

For convenience, the right-hand sides were designated a and b. Now easy to find

A

$A$ squaring the equalities and adding them:

A^{2} c o s^{2} (o m e g a) + A^{2} s i n^{2} (o m e g a) = a^{2} + b^{2}

$A ^ {2} \ cos ^ {2} (\ omega) + A ^ {2} \ sin ^ {2} (\ omega) = a ^ {2} + b ^ {2}$

A = p m s q r t a^{2} + b^{2}

$A = \ pm \ sqrt {a ^ {2} + b ^ {2}}$

You will probably need to select +, because

A

$A$ Is eccentricity. Well, God be with him, then if something can be re-designated in

e

$e$ .

Starting angle

o m e g a

$\ omega$ can be found by dividing one equation into another:

d f r a c A s i n (o m e g a) A c o s (o m e g a) = d f r a c b a,

$\ dfrac {A \ sin (\ omega)} {A \ cos (\ omega)} = \ dfrac {b} {a},$

t a n (o m e g a) = d f r a c b a,

$\ tan (\ omega) = \ dfrac {b} {a},$

o m e g a = a r c t a n (d f r a c b a),

$\ omega = \ arctan (\ dfrac {b} {a}),$

It seems they found everything, but now I would unravel the tangle with

a, b

$a, b$ :

\ begin {equation *}

\ begin {cases}

a = u_ {0} - \ dfrac {\ mu} {h ^ {2}},

\\

b = u ^ {'} _ {0}.

\ end {cases}

\ end {equation *}

We will analyze and recall that here who:

m u = G (m_{1} + m_{2})

$\ mu = G (m_ {1} + m_ {2})$

To find the rest, you need to determine the initial conditions in the polar system, they will be such (here already at the initial moment of time

t = 0

$t = 0$ ):

\ begin {equation *}

\ begin {cases}

\ rho (0) = \ rho_ {0},

\\

\ dot {\ rho} (0) = \ dot {\ rho} _ {0},

\\

\ phi (0) = \ phi_ {0},

\\

\ dot {\ phi} (0) = \ dot {\ phi} _ {0}. \\

\ end {cases}

\ end {equation *}

Then at any given time:

h = r h o^{2} d o t p h i

$h = \ rho ^ {2} \ dot {\ phi}$

In particular, the zero moment will determine the constant

h

$h$ :

h = r h o_{0}^{2} d o t {p h i}_{0}

$h = \ rho ^ {2} _ {0} \ dot {\ phi} _ {0}$

Moment of momentum at time zero (wordplay).

And finally:

u_{0} = d f r a c 1 r h o_{0}

$u_ {0} = \ dfrac {1} {\ rho_ {0}}$

And you need to tinker with the derivative a little bit:

u^{^{'}} = d f r a c d u d p h i = d f r a c d d p h i l e f t (d f r a c 1 r h o r i g h t) = - d f r a c 1 r h o^{2} d f r a c d r h o d p h i = - d f r a c 1 r h o^{2} d f r a c d r h o d t / d f r a c d p h i d t = - d f r a c 1 r h o^{2} d f r a c d o t r h o d o t p h i

$u ^ {'} = \ dfrac {du} {d \ phi} = \ dfrac {d} {d \ phi} \ left (\ dfrac {1} {\ rho} \ right) = - \ dfrac {1} {\ rho ^ {2}} \ dfrac {d \ rho} {d \ phi} = - \ dfrac {1} {\ rho ^ {2}} \ dfrac {d \ rho} {dt} / \ dfrac {d \ phi} {dt} = - \ dfrac {1} {\ rho ^ {2}} \ dfrac {\ dot {\ rho}} {\ dot {\ phi}}$

What we need:

u_{0}^{^{'}} = - d f r a c 1 r h o_{0}^{2} d f r a c d o t {r h o}_{0} d o t {p h i}_{0}

$u ^ {'} _ {0} = - \ dfrac {1} {\ rho ^ {2} _ {0}} \ dfrac {\ dot {\ rho} _ {0}} {\ dot {\ phi} _ {0}}$

It seems to be sorted out. But we didn’t start with the polar coordinate system. Not from her ... Still a little fuss will be.

How did we get into the polar. So:

\ begin {equation *}

\ begin {cases}

x = \ rho \ cos (\ phi),

\\

y = \ rho \ sin (\ phi).

\ end {cases}

\ end {equation *}

Back how? So (immediately at time zero):

\ begin {equation *}

\ begin {cases}

\ rho_ {0} = \ sqrt {x ^ {2} _ {0} + y ^ {2} _ {0}},

\\

\ phi_ {0} = \ arctan (\ dfrac {y_ {0}} {x_ {0}}).

\ end {cases}

\ end {equation *}

But if anyone remembers, we sent the axis last time

x

$x$ along

v e c r_{0}

$\ vec {r} _ {0}$ , and therefore it should be like this:

x_{0} = | v e c r_{0} |, y_{0} = 0

$x_ {0} = | \ vec {r} _ {0} |, y_ {0} = 0$

Respectively:

r h o_{0} = x_{0}, p h i_{0} = 0

$\ rho_ {0} = x_ {0}, \ phi_ {0} = 0$

Well, it’s not in vain that before that we took the initial angle to zero, in the sense here

u (0) = u (p h i = 0) .

$u (0) = u (\ phi = 0).$

With speeds, everything is also simple (we copy the formulas from the previous article):

\ begin {equation *}

\ begin {cases}

\ dot {x} = \ dot {\ rho} \ cos (\ phi) - \ rho \ sin (\ phi) \ dot {\ phi}

\\

\ dot {y} = \ dot {\ rho} \ sin (\ phi) + \ rho \ cos (\ phi) \ dot {\ phi}

\ end {cases}

\ end {equation *}

True, you need the opposite, here a linear system of equations, we solve:

\ begin {equation *}

\ begin {cases}

\ dot {\ rho} = \ dot {x} \ cos (\ phi) + \ dot {y} \ sin (\ phi)

\\

\ dot {\ phi} = \ dfrac {\ dot {y} \ cos (\ phi) - \ dot {x} \ sin (\ phi)} {\ rho}

\ end {cases}

\ end {equation *}

This can be used even when the initial angle is not zero, but in our case:

\ begin {equation *}

\ begin {cases}

\ dot {\ rho} _ {0} = \ dot {x} _ {0}

\\

\ dot {\ phi} _ {0} = \ dfrac {\ dot {y} _ {0}} {\ rho_ {0}}

\ end {cases}

\ end {equation *}

Well, then I will not paint as from the initial data

v e c r_{10}, v e c r_{20}, d o t {v e c r}_{10}, d o t {v e c r}_{20}

$\ vec {r} _ {10}, \ vec {r} _ {20}, \ dot {\ vec {r}} _ {10}, \ dot {\ vec {r}} _ {20}$ (we started with this) calculate

x_{0}, y_{0}, d o t x_{0}, d o t y_{0}

$x_ {0}, y_ {0}, \ dot {x} _ {0}, \ dot {y} _ {0}$ . I can only say that the next step will be to use the inverse transformation matrix; it was lost somewhere in previous articles. And so we will go back out of the plane into three-dimensional space. No matter how comfortable it was in two-dimensional, but we live in three-dimensional ...

That's all for today. To be continued…

Give us our daily bread today.

PayPal ($): what.is.truth.19@gmail.com

Bitcoin (BTC): 1AodAFYCbwrwTiZb5JVsQjv37G5toBcyQ

Ethereum Classic (ETC): 0x9234016395e0e6ef7cf6c0aa0f6f48f91ab39239

Ripple (XRP): rLW9gnQo7BQhU6igk5keqYnH3TVrCxGRzm (address), 270547561 (tag)

Bitcoin Cash (BCH): bitcoincash: qzxfz2hdcl0hv23a3hlcefsy07mglssjtgwrckhyg8

or webmoney (Below: Support the author -> Send money)

Not as holy as the Lord; for there is none other than Thee; and there is no rock like our God.

Do not multiply the speeches of the arrogant; bold words do not come from your mouth; for the Lord is the God of knowledge, and His affairs are balanced.

The bow of the strong is refracted, and the weak are girded by force;

the well-fed work from bread, and the hungry rest; even the barren gives birth seven times, and the multi-child gives birth to exhaustion.

The Lord kills and quickens, brings down to the netherworld and raises;

The Lord makes a beggar and enriches, humiliates and exalts.

He will lift the poor out of the dust, exalt the beggar out of tribe, planting with the nobles, and he will give them the throne of glory; for the Lord has the foundation of the earth, and He established the universe upon them.

He watches the feet of His saints, but the wicked in the darkness disappear; for man is not strong by force.

The Lord will destroy the disputes with Him; thunder from heaven thunder upon them. The Lord will judge the ends of the earth, and give fortress to his king, and exalt his anointed horn.

1 Samuel 2

All Articles

We design a space rocket from scratch. Part 5 - Kepler's First Law

Content

More articles: